Đề bài
Một hình vuông có cạnh là a + b (với a > 0 và b > 0).
- Hãy viết biểu thức tính diện tích hình vuông.
- Áp dụng phép nhân đa thức với đa thức để tính diện tích hình vuông theo a và b.
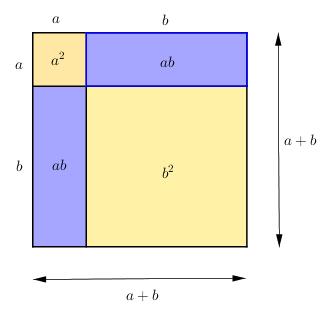
- Quan sát hình vẽ bên để biểu diễn diện tích hình vuông theo diện tích các hình hợp thành nó.
- Tính diện tích hình vuông với a = 5, b = 3.
Lời giải chi tiết
Diện tích hình vuông \(\left( {a + b} \right)\left( {a + b} \right) = {\left( {a + b} \right)^2}\)
Ta có: \(\left( {a + b} \right)\left( {a + b} \right) = {a^2} + ab + ab + {b^2} = {a^2} + 2ab + {b^2}\)
Diện tích hình vuông \({a^2} + ab + ab + {b^2} = {a^2} + 2ab + {b^2}\)
Với \(a = 5;\,\,b = 3\) diện tích hình vuông là \({\left( {5 + 3} \right)^2} = {8^2} = 64\)
soanvan.me
