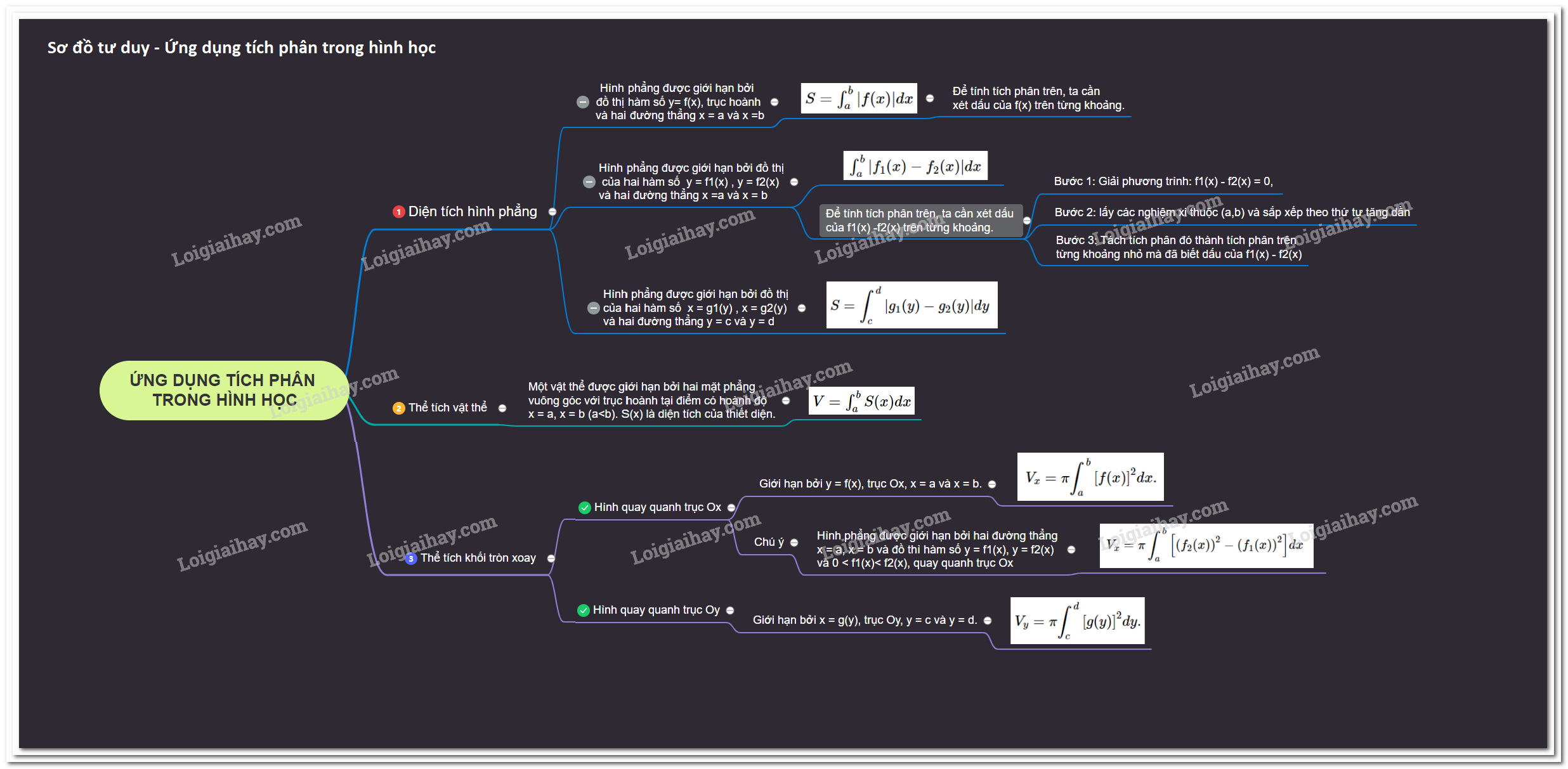
1. Tính diện tích hình phẳng
a) Nếu hình phẳng được giới hạn bởi đồ thị hàm số \(y = f(x)\) liên tục trên đoạn \([a;b]\); trục hoành và hai đường thẳng \(x = a; x = b\), thì diện tích \(S\) được cho bởi công thức:
\(S = \int_a^b {\left| {f(x)} \right|} dx\) (1)
Chú ý: Để tính tích phân trên, ta xét dấu của \(f(x)\) trên đoạn \([a,b]\). Nếu \(f(x)\) không đổi dấu trên khoảng \((c;d) ⊂ [a;b]\) thì :
\(\int_c^d {\left| {f(x)} \right|} dx = \left| {\int_c^d f (x)dx} \right|\)
Chẳng hạn ta có:
\(\int_a^b {\left| {f(x)} \right|} dx = \left| {\int_a^{{c_1}} f (x)dx} \right| + \left| {\int_{{c_1}}^{{c_2}} f (x)dx} \right| \)\(+ \left| {\int_{{c_2}}^{{c_3}} f (x)dx} \right| + \left| {\int_{{c_3}}^b f (x)dx} \right|\)
b) Nếu hình phẳng được giới hạn bởi đồ thị của hai hàm số \(y = {\rm{ }}{f_1}\left( x \right)\) và \(y = {\rm{ }}{f_2}\left( x \right)\) liên tục trên đoạn [a;b] và hai đường thẳng \( x = a, x = b\) thì diện tích \(S\) được cho bởi công thức :
\(\int_a^b {\left| {{f_1}(x) - {f_2}(x)} \right|} dx\) (2)
Chú ý: Để tính tích phân trên, ta xét dấu \(f\left( x \right) = \;{f_1}\left( x \right){\rm{ }}\; - {\rm{ }}{f_2}\left( x \right)\) trên đoạn \([a;b]\) hoặc tìm nghiệm của nó trên khoảng \((a;b)\), sau đó áp dụng tính chất nêu ở chú ý trên. Cụ thể ta thực hiện các bước sau:
Bước 1: Giải phương trình: \({f_1}\left( x \right){\rm{ }}\; - {\rm{ }}{f_2}\left( x \right){\rm{ }} = {\rm{ }}0\), tìm các nghiệm \({x_i}\; \in {\rm{ }}\left( {a;b} \right)\)
Bước 2 : Sắp xếp các nghiệm theo thứ tự tăng dần, chẳng hạn có n nghiệm:
\[{x_{1\;}} < {\rm{ }}{x_2}\; < {\rm{ }} \ldots {\rm{ }} < {\rm{ }}{x_{n.}}\]
Bước 3: Tính diện tích theo công thức (*):
\(S = \int_a {^b} \left| {f(x)} \right|dx = \left| {\int_a^{{x_1}} f (x)dx} \right| + \left| {\int_{{x_1}}^{{x_2}} f (x)dx} \right| + ... + \left| {\int_{{x_n}}^b f (x)dx} \right|\)
Nếu hình phẳng nói trên không cho giới hạn bởi hai đường thẳng \(x = a, x = b\) thì ta tìm các nghiệm trên tập xác định và trong công thức (*), a được thay thế bởi \({x_1}\), b được thay thế bởi \({x_n}\).
Công thức (1) là trường hợp đặc biệt của công thức (2) khi \(y{\rm{ }} = {\rm{ }}{f_1}\left( x \right) = {\rm{ }}0\) hoặc \(y{\rm{ }} = {\rm{ }}{f_2}\left( x \right){\rm{ = }}0\)
Tương tự, hình phẳng được giới hạn bởi đồ thị hàm số \(\;x{\rm{ }} = {\rm{ }}{g_1}\left( y \right),\;x{\rm{ }} = {\rm{ }}{g_2}\left( y \right)\) liên tục trên đoạn \([c;d]\) và hai đường thẳng \(y = c, y = d\) có diện tích được cho bởi công thức: $$S = \int_c^d {\left| {{g_1}(y) - {g_2}(y)} \right|} dy$$
2. Thể tích vật thể
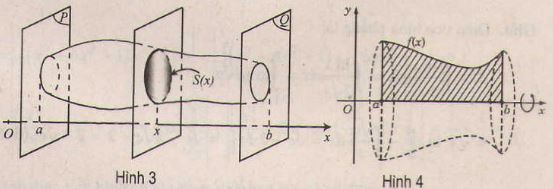
Một vật thể được giới hạn bởi hai mặt phẳng vuông góc với trục hoành tại điểm có hoành độ \(x = a, x = b (a<b)\). \(S(x)\) là diện tích của thiết diện. Thể tích của vật thể được cho bởi công thức: \(V = \int_a^b S (x)dx\) (với \(S(x)\) là hàm số không âm, liên tục trên đoạn \([a;b]\)).
3. Thể tích khối tròn xoay
a) Hình phẳng quay quanh trục \(Ox\): Cho hình phẳng được giới hạn bởi đồ thị hàm số \(y = f(x)\) không âm và liên tục trên đoạn \([a;b]\), trục \(Ox\) và hai đường thẳng \(x = a, x = b\) quay quanh trục \(Ox\), ta được khối tròn xoay (h.4). Thể tích \({V_x}\) của khối tròn xoay này được cho bởi công thức: $${V_x} = \pi {\int_a^b {\left[ {f(x)} \right]} ^2}dx.$$
b) Hình phẳng quay quanh trục \(Oy\) (kiến thức bổ sung): Cho hình phẳng được giới hạn bởi đồ thị hàm số \(x = g(y)\) không âm và liên tục trên đoạn \([c;d]\), trục \(Oy\) và hai đường thẳng \(y = c, y = d\) quay quanh trục \(Oy\), ta được khối tròn xoay. Thể tích Vy của khối tròn xoay này được cho bởi công thức: $${V_y} = \pi {\int_c^d {\left[ {g(y)} \right]} ^2}dy.$$
Chú ý. Thể tích của vật thể tạo bởi hình phẳng được giới hạn bởi hai đường thẳng \(x = a\), \(x = b\) và đồ thị hàm số \(y{\rm{ }} = {\rm{ }}{f_1}\left( x \right),{\rm{ }}y{\rm{ }} = {\rm{ }}{f_2}\left( x \right)\) liên tục và \(0\; \le \;\;{f_1}\left( x \right)\; \le {\rm{ }}{f_2}\left( x \right)\) trên đoạn \([a;b]\) quay quanh trục \(Ox\) được cho bởi công thức: $${V_x} = \pi \int_a^b {\left[ {{{({f_2}(x))}^2} - {{({f_1}(x))}^2}} \right]} dx$$
Tương tự, đổi vai trò \(x\) và \(y\) cho nhau, ta có công thức tính \({V_y}\) (khi hình phẳng quay quanh trục \(Oy\)).
soanvan.me
