Chọn khẳng định đúng. Góc ở tâm là góc
-
A
Có đỉnh nằm trên đường tròn
-
B
Có đỉnh trùng với tâm đường tròn
-
C
Có hai cạnh là hai đường kính của đường tròn
-
D
Có đỉnh nằm trên bán kính của đường tròn
Đáp án của giáo viên lời giải hay : B
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
-
A
Số đo cung lớn
-
B
Số đo của góc ở tâm chắn cung đó
-
C
Số đo của góc ở tâm chắn cung lớn
-
D
Số đo của cung nửa đường tròn
Đáp án của giáo viên lời giải hay : B
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn
-
A
Có số đo lớn hơn
-
B
Có số đo nhỏ hơn $90^\circ $
-
C
Có số đo lớn hơn $90^\circ $
-
D
Có số đo nhỏ hơn
Đáp án của giáo viên lời giải hay : D
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn thì có số đo nhỏ hơn.
Cho hai tiếp tuyến tại $A$ và $B$ của đường tròn \(\left( O \right)\) cắt nhau tại M, biết \(\widehat {AMB} = {50^0}\) .
Tính \(\widehat {AMO}\) và \(\widehat {BOM}\)
-
A
$\widehat {AMO} = 35^\circ ;\widehat {MOB} = 55^\circ $
-
B
$\widehat {AMO} = 65^\circ ;\widehat {MOB} = 25^\circ $
-
C
$\widehat {AMO} = 25^\circ ;\widehat {MOB} = 65^\circ $
-
D
$\widehat {AMO} = 55^\circ ;\widehat {MOB} = 35^\circ $
Đáp án của giáo viên lời giải hay : C
Sử dụng tính chất hai tiếp tuyến cắt nhau
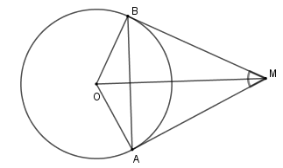
Vì $MA,MB$ là hai tiếp tuyến của đường tròn $\left( O \right)$ nên $OM$ là tia phân giác của $\widehat {AOB}$; $MO$ là tia phân giác của $\widehat {AMB}$ hay $\widehat {AMO} = \dfrac{1}{2}\widehat {AMB} = \dfrac{{50^\circ }}{2} = 25^\circ $.
Mà tam giác $OAM$ vuông tại $A$ (do $MA$ là tiếp tuyến) nên $\widehat {MOA} = 90^\circ - \widehat {AMO} = 65^\circ $
Mà $OM$ là tia phân giác của $\widehat {AOB}$ nên $\widehat {MOB} = \widehat {MOA} = 65^\circ $.
Vậy $\widehat {AMO} = 25^\circ ;\widehat {MOB} = 65^\circ. $
Số đo cung \(AB\) nhỏ và số đo cung \(AB\) lớn lần lượt là
-
A
$130^\circ ;250^\circ $
-
B
$130^\circ ;230^\circ $
-
C
$230^\circ ;130^\circ $
-
D
$150^\circ ;210^\circ $
Đáp án của giáo viên lời giải hay : B
Sử dụng định lý tổng các góc trong tứ giác và số đo cung.
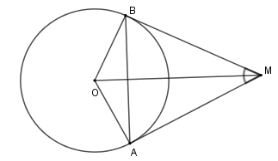
Xét tứ giác $OAMB$ có
$\widehat {BOA} + \widehat {OBM} + \widehat {OAM} + \widehat {AMB} = 360^\circ \Rightarrow \widehat {BOA} = 360^\circ - 90^\circ - 90^\circ - 50^\circ = 130^\circ $
Suy ra số đo cung nhỏ $AB$ là $130^\circ $; số đo cung lớn $AB$ là $360^\circ - 130^\circ = 230^\circ $.
Cho tam giác $ABC$ đều nội tiếp đường tròn $\left( O \right)$. Tính số đo cung $AC$ lớn.
-
A
$240^\circ $
-
B
$120^\circ $
-
C
$360^\circ $
-
D
$210^\circ $
Đáp án của giáo viên lời giải hay : A
Sử dụng định lý tổng các góc trong tam giác và số đo cung.
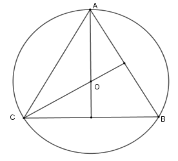
Vì tam giác $ABC$ đều có $O$ là tâm đường tròn ngoại tiếp nên $O$ cũng là giao ba đường phân giác nên $AO;CO$ lần lượt là các đường phân giác $\widehat {BAC}$; $\widehat {ACB}$.
Ta có $\widehat {CAO} = \dfrac{1}{2}\widehat {BAC} = \dfrac{{60^\circ }}{2} = 30^\circ $;$\widehat {ACO} = \dfrac{1}{2}\widehat {ACB} = \dfrac{{60^\circ }}{2} = 30^\circ $
Xét tam giác $AOC$ có $\widehat {AOC} = 180^\circ - \widehat {CAO} - \widehat {ACO} = 120^\circ $ nên số đo cung nhỏ $AC$ là $120^\circ $.
Do đó số đo cung lớn $AC$ là $360^\circ - 120^\circ = 240^\circ $.
Cho đường tròn \(\left( {O;R} \right)\), lấy điểm \(M\) nằm ngoài \(\left( O \right)\) sao cho \(OM = 2R.\) Từ M kẻ tiếp tuyến \(MA\) và \(MB\) với \(\left( O \right)\) (\(A,B\) là các tiếp điểm).
Số đo góc $\widehat {AOM}$ là
-
A
$30^\circ $
-
B
$120^\circ $
-
C
$50^\circ $
-
D
$60^\circ $
Đáp án của giáo viên lời giải hay : D
Sử dụng tỉ số lượng giác của góc nhọn
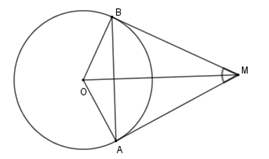
Xét tam giác $AOM$ vuông tại $A$ ta có $\cos \widehat {AOM} = \dfrac{{OA}}{{OM}} = \dfrac{R}{{2R}} = \dfrac{1}{2} \Rightarrow \widehat {AOM} = 60^\circ .$
Số đo cung \(AB\) nhỏ là
-
A
$240^\circ $
-
B
$120^\circ $
-
C
$360^\circ $
-
D
$210^\circ $
Đáp án của giáo viên lời giải hay : B
Sử dụng tính chất hai tiếp tuyến cắt nhau và số đo cung
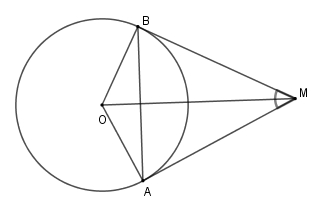
Xét đường tròn $\left( O \right)$ có $MA;MB$ là hai tiếp tuyến cắt nhau tại $M$ nên $OM$ là tia phân giác của góc $\widehat {AOB}$
Suy ra $\widehat {AOB} = 2\widehat {AOM} = 2.60^\circ = 120^\circ $ mà $\widehat {AOB}$ là góc ở tâm chắn cung \(AB\)
Nên số đo cung nhỏ \(AB\) là $120^\circ $.
Cho \(\left( {O;R} \right)\) và dây cung \(MN = R\sqrt 3 .\) Kẻ \(OI\) vuông góc với \(MN\) tại $I$ .
Tính độ dài \(OI\) theo $R$ .
-
A
$\dfrac{{R\sqrt 3 }}{3}$
-
B
$\dfrac{R}{{\sqrt 2 }}$
-
C
$\dfrac{R}{3}$
-
D
$\dfrac{R}{2}$
Đáp án của giáo viên lời giải hay : D
Sử dụng liên hệ giữa đường kính và dây cung.
Sử dụng định lý Pytago.
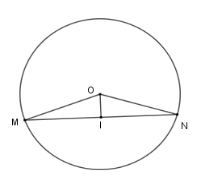
Xét $\left( O \right)$ có $OI \bot MN$ tại $I$ nên $I$ là trung điểm của dây $MN$ (đường kính vuông góc với dây thì đi qua trung điểm của dây đó) $ \Rightarrow MI = IN=\dfrac{MN}2 = \dfrac{{\sqrt 3 R}}{2}$
Xét tam giác $OIM$ vuông tại $I$, theo định lý Pytago ta có $O{I^2} = O{M^2} - M{I^2}$
$\Rightarrow OI = \sqrt {{R^2} - {{\left( {\dfrac{{\sqrt 3 R}}{2}} \right)}^2}} $$= \sqrt {{R^2} - \dfrac{{ 3 R^2}}{4}} =\sqrt { \dfrac{ R^2}{4}}= \dfrac{R}{2}$
Tính số đo cung nhỏ $MN.$
-
A
$120^\circ $
-
B
$150^\circ $
-
C
$90^\circ $
-
D
$145^\circ $
Đáp án của giáo viên lời giải hay : A
Sử dụng tỉ số lượng giác của góc nhọn và số đo cung
“Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó”
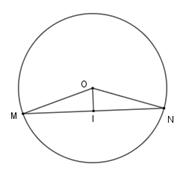
Xét tam giác $OIM$ vuông tại $I$ ta có $\sin \widehat {MOI} = \dfrac{{MI}}{{MO}} = \dfrac{{\sqrt 3 R}}{2}:R = \dfrac{{\sqrt 3 }}{2} \Rightarrow \widehat {MOI} = 60^\circ $
$\Delta MON$ cân tại $O$ có $OI$ vừa là đường cao vừa là đường phân giác nên $\widehat {MON} = 2\widehat {MOI} = 2.60^\circ = 120^\circ $
Suy ra số đo cung nhỏ $MN$ là $120^\circ $.
Cho tam giác \(ABC\) cân tại $A$ . Vẽ đường tròn tâm $O$, đường kính \(BC\). Đường tròn \(\left( O \right)\) cắt $AB$, $AC$ lần lượt tại \(I,K.\)
So sánh các cung nhỏ $BI$ và cung nhỏ $CK$
-
A
Số đo cung nhỏ $BI$ bằng số đo cung nhỏ $CK$
-
B
Số đo cung nhỏ $BI$ nhỏ hơn số đo cung nhỏ $CK$
-
C
Số đo cung nhỏ $BI$ lớn hơn số đo cung nhỏ $CK$
-
D
Số đo cung nhỏ $BI$ bằng hai lần số đo cung nhỏ $CK$
Đáp án của giáo viên lời giải hay : A
Sử dụng tam giác bằng nhau
So sánh hai cung
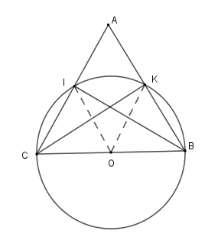
Xét các tam giác $\Delta IBC$ và .$\Delta KBC$ có $BC$ là đường kính của $\left( O \right)$ và $I;K \in \left( O \right)$
Nên $\Delta IBC$ vuông tại $I$ và $\Delta KBC$ vuông tại $K$
Xét hai tam giác vuông $\Delta IBC$ và .$\Delta KBC$ ta có $BC$ chung; $\widehat {ACB} = \widehat {ABC}$ (do$\Delta ABC$ cân)
$ \Rightarrow \Delta IBC = \Delta KCB\left( {ch - gn} \right) \Rightarrow IB = CK$
Suy ra $\Delta COK = \Delta IOB\left( {c - c - c} \right)$$ \Rightarrow \widehat {COK} = \widehat {IOB}$ suy ra số đo hai cung nhỏ $CK$ và $BI$ bằng nhau.
Tính $\widehat {IOK}$ biết $\widehat {BAC} = 40^\circ $
-
A
$80^\circ $
-
B
$100^\circ $
-
C
$60^\circ $
-
D
$40^\circ $
Đáp án của giáo viên lời giải hay : B
Sử dụng tổng các góc trong tam giác
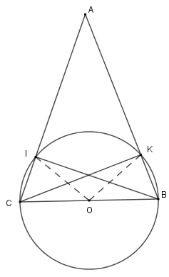
Xét tam giác $ABC$ cân tại $A$ có $\widehat A = 40^\circ \Rightarrow \widehat {KBO} = \widehat {ICO} = 70^\circ $
Xét tam giác $OKB$cân tại $O$ có $\widehat {KBO} = 70^\circ \Rightarrow \widehat {KOB} = 180^\circ - 2.70^\circ = 40^\circ $
Tương tự ta có $\widehat {IOC} = 40^\circ $
Suy ra $\widehat {IOK} = 180^\circ - 40^\circ - 40^\circ = 100^\circ $
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là trung điểm của bán kính \(OA\). Dây \(CD\) vuông góc với \(OA\) tại $H$ . Tính số đo cung lớn \(CD.\)
-
A
$260^\circ $
-
B
$300^\circ $
-
C
$240^\circ $
-
D
$120^\circ $
Đáp án của giáo viên lời giải hay : C
+) Sử dụng liên hệ giữa đường kính và dây
+) Kiến thức về số đo cung
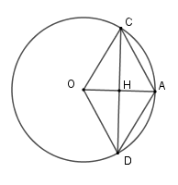
Xét đường tròn$\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD$
Tứ giác $OCAD$ có hai đường chéo vuông góc và giao nhau tại trung điểm mỗi đường nên $OCAD$ là hình thoi.
$ \Rightarrow OC = CA$ mà $OC = OA$ nên $OC = OA = AC$ hay tam giác $OAC$ đều $ \Rightarrow \widehat {COA} = 60^\circ \Rightarrow \widehat {COD} = 120^\circ $
Do đó số đo cung nhỏ $CD$ là $120^\circ $ và số đo cung lớn $CD$ là $360^\circ - 120^\circ = 240^\circ $.
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 55^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
-
A
$55^\circ $
-
B
$60^\circ $
-
C
$40^\circ $
-
D
$50^\circ $
Đáp án của giáo viên lời giải hay : A
Bước 1: Chứng minh $E;O;C$ thẳng hàng
Bước 2: Tính số đo cung thông qua góc ở tâm
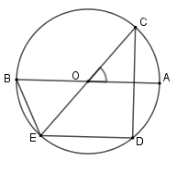
Xét $\left( O \right)$ có $CD \bot OA;ED{\rm{//}}OA \Rightarrow CD \bot ED$ hay $\widehat {EDC} = 90^\circ $ mà $E;D;C \in \left( O \right)$ nên $EC$ là đường kính của $\left( O \right)$ hay $E;O;C$ thẳng hàng.
Do đó $\widehat {BOE} = \widehat {COA} = 55^\circ $ (đối đỉnh) nên số đo cung nhỏ $BE$ là $55^\circ $.
