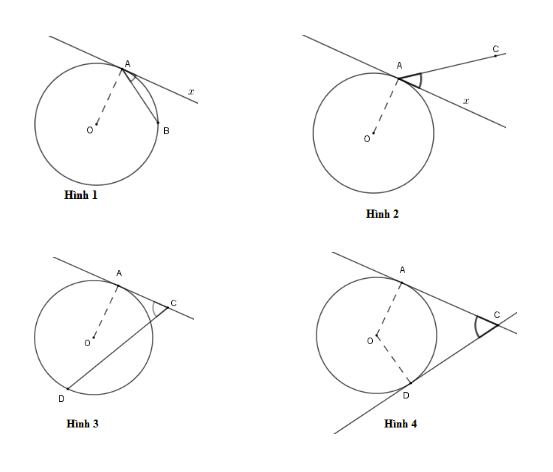
Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung?
-
A
Hình $1$
-
B
Hình $2$
-
C
Hình $3$
-
D
Hình $4$
Đáp án của giáo viên lời giải hay : A
Cho đường tròn tâm \((O)\) có \(Ax\) là tia tiếp tuyến tại tiếp điểm $A$ và dây cung $AB.$ Khi đó, góc \(BAx\)là góc tạo bởi tia tiếp tuyến và dây cung.
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng
-
A
\(90^\circ \)
-
B
Số đo góc ở tâm chắn cung đó
-
C
Nửa số đo của góc nội tiếp chắn cung đó
-
D
Nửa số đo của cung bị chắn
Đáp án của giáo viên lời giải hay : D
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng nửa số đo cung bị chắn
Kết luận nào sau đây là đúng.
-
A
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo lớn hơn số đo góc nội tiếp chắn cung đó.
-
B
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo nhỏ hơn số đo góc nội tiếp chắn cung đó.
-
C
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
-
D
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng hai lần số đo của góc nội tiếp chắn cung đó.
Đáp án của giáo viên lời giải hay : C
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) . Trên tia đối của tia \(AB\) lấy điểm \(M\) . Vẽ tiếp tuyến \(MC\) với nửa đường tròn. Gọi \(H\) là hình chiếu của \(C\) trên \(AB\) .
\(CA\) là tia phân giác của góc nào dưới đây
-
A
\(\widehat {MCB}\)
-
B
\(\widehat {MCH}\)
-
C
\(\widehat {MCO}\)
-
D
\(\widehat {CMB}\)
Đáp án của giáo viên lời giải hay : B
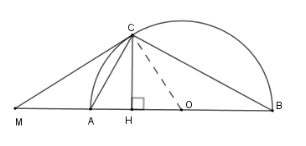
Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA}\) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ACH\) vuông tại \(H\) có \(\widehat {ACH}+ \widehat {CAH}=90^0\) (1)
Xét tam giác \(ACB\) vuông tại \(C\) có \(\widehat {CBA}+ \widehat {CAH}=90^0\) (2)
Từ (1) và (2) suy ra \(\widehat {ACH} = \widehat {CBA}\) (**) (cùng phụ với góc \(\widehat {CAB}\) )
Từ (*) và (**) ta có \(\widehat {MCA} = \widehat {ACH}\) nên \(CA\) là tia phân giác của góc \(\widehat {MCH}\) .
Giả sử \(OA = a;MC = 2a\) . Độ dài \(CH\) là
-
A
\(\dfrac{{\sqrt 5 a}}{5}\)
-
B
\(\dfrac{{2a}}{5}\)
-
C
\(\dfrac{{2\sqrt 5 a}}{5}\)
-
D
\(\dfrac{{3\sqrt 5 a}}{5}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông
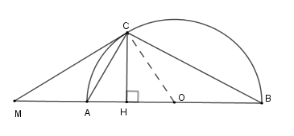
Theo định lý Pytago cho tam giác \(MCO\) vuông ta có \(MO = \sqrt {O{C^2} + M{C^2}} = a\sqrt 5 \)
Xét tam giác \(MCO\) vuông ta có \(MC.CO = CH.MO \Rightarrow CH = \dfrac{{2{a^2}}}{{\sqrt 5 a}} = \dfrac{{2\sqrt 5 a}}{5}\) .
Từ điểm \(M\) nằm ngoài \(\left( O \right)\) kẻ các tiếp tuyến \(MD;MB\) và cát tuyến \(MAC\) với đường tròn. (\(A\) nằm giữa \(M\) và \(C\) )
Khi đó \(MA.MC\) bằng
-
A
\(M{B^2}\)
-
B
\(B{C^2}\)
-
C
\(MD.MA\)
-
D
\(MB.MC\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng.
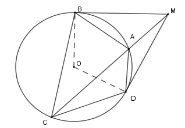
Xét \(\left( O \right)\) có \(\widehat {MBA} = \widehat {BCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AB\) )
Suy ra \(\Delta MBA\backsim\Delta MCB\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{MB}}{{MC}} = \dfrac{{MA}}{{MB}} = \dfrac{{BA}}{{CB}} \)
\(\Rightarrow MA.MC = M{B^2}\)
Hệ thức nào dưới đây là đúng.
-
A
\(AB.CD = AD.BM\)
-
B
\(AB.CD = AD.BC\)
-
C
\(AB.CD = AM.BC\)
-
D
\(AB.CD = MD.MC\)
Đáp án của giáo viên lời giải hay : B
Sử dụng hai tam giác đồng dạng và tính chất hai tiếp tuyến cắt nhau. Từ đó suy ra hệ thức cần tìm .
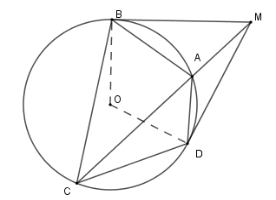
Tương tự câu trước ta có \(\Delta MAD\backsim \Delta MDC\left( {g - g} \right) \)\(\Rightarrow \dfrac{{MD}}{{MC}} = \dfrac{{AD}}{{DC}}\)
Mà theo câu trước ta có \(\dfrac{{MB}}{{MC}} = \dfrac{{BA}}{{CB}}\)
Theo tính chất hai tiếp tuyến cắt nhau thì \(MB = MD\) nên \(\dfrac{{AD}}{{DC}} = \dfrac{{AB}}{{BC}} \Leftrightarrow AD.BC = AB.DC\)
Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\), tiếp tuyến tại ${\rm{A}}$ của\((O)\) cắt $BC$ tại $P$ .
Hai tam giác nào sau đây đồng dạng?
-
A
\(\Delta PAB\backsim\Delta ABC\)
-
B
\(\Delta PAC\backsim\Delta PBA\)
-
C
\(\Delta PAC\backsim\Delta ABC\)
-
D
\(\Delta PAC\backsim\Delta PAB\)
Đáp án của giáo viên lời giải hay : B
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng.
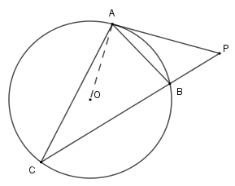
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {BAP}\) (hệ quả) suy ra \(\Delta PAC\backsim\Delta PBA\left( {g - g} \right)\) .
Tia phân giác trong góc $A$ cắt $BC$ và \((O)\) lần lượt tại $D$ và $M$. Khi đó \(MA.MD\) bằng
-
A
\(M{B^2}\)
-
B
\(2M{C^2}\)
-
C
\(A{B^2}\)
-
D
\(A{C^2}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hệ quả góc nội tiếp để và tính chất tia phân giác để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng.
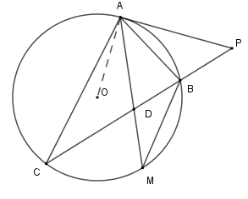
Xét đường tròn \((O)\) có \(\widehat {MBC} = \widehat {MAC}\) (hai góc nội tiếp cùng chắn cung MC)
Lại có \(\widehat {MAB} = \widehat {MAC}\) (do AM là phân giác góc BAC)
Suy ra \(\widehat {MBD} = \widehat {MAB}\) (cùng bằng \(\widehat {MAC}\) )
Xét \(\Delta MBD\) và \(\Delta MAB\) có \(\widehat M\) chung và \(\widehat {MBD} = \widehat {MAB}\) (chứng minh trên)
Nên \(\Delta MBD\backsim\Delta MAB\left( {g - g} \right) \)\(\Rightarrow \dfrac{{MB}}{{MA}} = \dfrac{{MD}}{{MB}} \)\(\Rightarrow MA.MD = M{B^2}\)
Cho nửa đường tròn $(O)$ đường kính $AB$ và một điểm $C$ trên nửa đường tròn. Gọi $D$ là một điểm trên đường kính $AB$; qua $D$ kẻ đường vuông góc với $AB$ cắt $BC$ tại $F$, cắt $AC$ tại $E$. Tiếp tuyến của nửa đường tròn tại $C$cắt $EF$ tại $I.$Khi đó
-
A
\(IE = IF\)
-
B
\(IE = 2IF\)
-
C
$EF = 3IE$
-
D
\(EF = 3IF\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau.
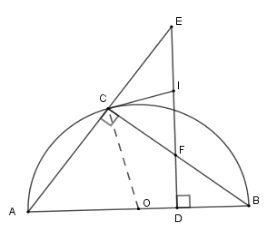
Xét \(\left( O \right)\) có $\widehat {ICB} = \widehat {CAB}$ (hệ quả) mà $\widehat {BFD} = \widehat {BAC}$ (cùng phụ với \(\widehat {ABC}\) )
Nên \(\widehat {ICF} = \widehat {BFD} \Rightarrow \widehat {ICF} = \widehat {CFI}\) suy ra \(\Delta ICF\) cân tại \(I \Rightarrow IF = IC\) (*)
Lại có \(\widehat {ICE} + \widehat {ICF} = 90^\circ \Rightarrow \widehat {ICE} + \widehat {CAB} = 90^\circ \) mà \(\widehat {CAB} + \widehat {AED} = 90^\circ \Rightarrow \widehat {CEI} = \widehat {ECI} \Rightarrow \Delta ICE\) cân tại \(I\)
Nên \(IE = IC\) (**)
Từ (*) và (**) suy ra \(IE = IF = \dfrac{{EF}}{2}\) .
Cho đường tròn $(O;R)$ với $A$ là điểm cố định trên đường tròn. Kẻ tiếp tuyến $Ax$ với $(O)$ và lấy $M$ là điểm bất kì thuộc tia $Ax$. Vẽ tiếp tuyến thứ hai $MB$ với đường tròn $(O)$. Gọi $I$ là trung điểm $MA$, $K$ là giao điểm của $BI$ với $(O)$.
Tam giác \(IKA\) đồng dạng với tam giác
-
A
\(IBA\)
-
B
\(IAB\)
-
C
\(ABI\)
-
D
\(KAB\)
Đáp án của giáo viên lời giải hay : B
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng.
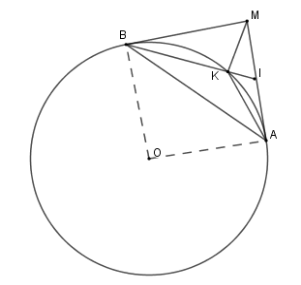
Ta có \(\widehat {IAK} = \widehat {IBA}\) (hệ quả) nên \(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\)
Tam giác nào dưới đây đồng dạng với tam giác \(IKM\)?
-
A
\(IMB\)
-
B
\(MIB\)
-
C
\(BIM\)
-
D
\(MBI\)
Đáp án của giáo viên lời giải hay : A
Sử dụng kết quả câu trước: \(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\)
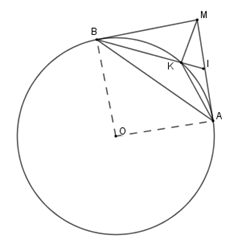
\(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\) (câu trước) \( \Rightarrow \dfrac{{IK}}{{IA}} = \dfrac{{IA}}{{IB}}\) mà \(IA = IM \Rightarrow \dfrac{{IK}}{{IM}} = \dfrac{{IM}}{{IB}}\) nên \(\Delta IKM\backsim\Delta IMB\left( {c - g - c} \right)\)
Giả sử $MK$cắt $(O)$ tại $C$. Đường thẳng \(MA\) song song với đường thẳng
-
A
\(BO\)
-
B
\(BC\)
-
C
\(KB\)
-
D
\(OC\)
Đáp án của giáo viên lời giải hay : B
Sử dụng câu vừa xong và hệ quả về góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
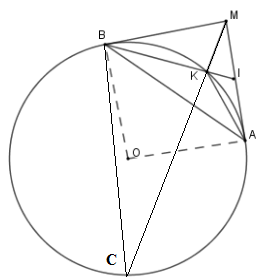
Vì \(\Delta IKM\backsim\Delta IMB\left( {c - g - c} \right)\) \( \Rightarrow \widehat {IMK} = \widehat {MBI}\) mà \(\widehat {MBI} = \widehat {MCB}\) (hệ quả)
Nên \(\widehat {BCM} = \widehat {CMA}\) mà hai góc ở vị trí so le trong nên \(MA{\rm{//}}BC\) .
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
-
A
\(A{B^2}\)
-
B
\(B{C^2}\)
-
C
\(A{C^2}\)
-
D
\(A{M^2}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
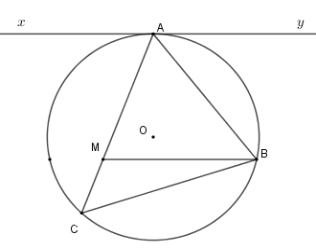
Ta có \(\widehat {yAB} = \widehat {ACB}\) (hệ quả) mà \(\widehat {yAB} = \widehat {ABM}\) (so le trong) nên \(\widehat {ACB} = \widehat {ABM} \Rightarrow \Delta AMB\backsim\Delta ABC\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow AM.AC = A{B^2}\) .
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\) nội tiếp \(\left( {O;R} \right)\) . Gọi \(BD;CE\) là hai đường cao của tam giác. Gọi \(d\) là tiếp tuyến tại \(A\) của \(\left( {O;R} \right)\) và \(M,N\) lần lượt là hình chiếu của \(B,C\) trên \(d\) .
Tam giác \(AMB\) đồng dạng với tam giác
-
A
\(BCD\)
-
B
\(CBD\)
-
C
\(CDB\)
-
D
\(BDC\)
Đáp án của giáo viên lời giải hay : C
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng.
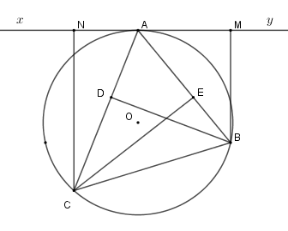
Xét \(\left( O \right)\) có \(\widehat {MAB} = \widehat {ACB}\) (hệ quả) \( \Rightarrow \Delta AMB\backsim\Delta CDB\left( {g - g} \right)\)
Hệ thức nào dưới đây đúng .
-
A
\(\dfrac{{AB}}{{AC}} = \dfrac{{ME.BA}}{{NA.CD}}\)
-
B
\(\dfrac{{AB}}{{AC}} = \dfrac{{MA.BA}}{{NA.CD}}\)
-
C
\(\dfrac{{AB}}{{AC}} = \dfrac{{M{A^2}}}{{NA.CD}}\)
-
D
\(\dfrac{{AB}}{{AC}} = \dfrac{{MA.BE}}{{NA.CD}}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng câu trước và các tam giác đồng dạng
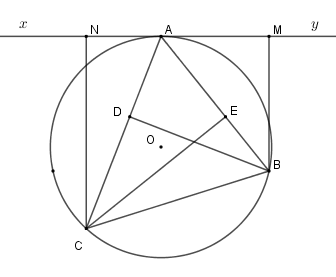
Từ câu trước, ta có \(\dfrac{{AM}}{{CD}} = \dfrac{{AB}}{{CB}}\)
Tương tự ta có \(\Delta ANC\backsim\Delta BEC\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{BE}}{{AN}} = \dfrac{{BC}}{{AC}}\)
Suy ra \(\dfrac{{AM}}{{CD}}.\dfrac{{BE}}{{AN}} = \dfrac{{AB}}{{BC}}.\dfrac{{BC}}{{AC}}\)
\(\Leftrightarrow \dfrac{{AB}}{{AC}} = \dfrac{{MA.BE}}{{NA.CD}}\)
Cho nửa đường tròn $\left( O \right)$ đường kính $AB$. Trên tia đối của tia $AB$ lấy một điểm $M$. Vẽ tiếp tuyến $MC$ với nửa đường tròn. Gọi $H$ là hình chiếu của $C$ lên $AB$. Biết $MC = a,MB = 3a$. Độ dài đường kính $AB$ là?
-
A
$AB = 2a$
-
B
$AB = \dfrac{{10a}}{3}$
-
C
$AB = \dfrac{{8a}}{3}$
-
D
$AB = 3a$
Đáp án của giáo viên lời giải hay : C
Chứng minh đẳng thức \(M{C^2} = MA.MB \Rightarrow MA \Rightarrow AB\).
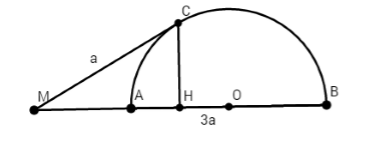
Ta có \(\widehat {MCA} = \widehat {CBA}\) (cùng chắn cung \(AC\))
Xét \(\Delta ACM\) và \(\Delta CBM\) có:
\(\widehat {MCA} = \widehat {CBA}\) (cmt)
\(\widehat M\) chung
Suy ra \(\Delta ACM \backsim \Delta CBM\) (g.g)
$\begin{array}{l} \Rightarrow M{C^2} = MA.MB\\ \Rightarrow MA = \dfrac{{{a^2}}}{{3a}} = \dfrac{a}{3}\\ \Rightarrow AB = MB - MA = 3a - \dfrac{a}{3} = \dfrac{{8a}}{3}\end{array}$
cho đường tròn $\left( {O;R} \right)$ có hai đường kính $AB$ và $CD$ vuông góc. Gọi $I$ là điểm trên cung $AC$ sao cho khi vẽ tiếp tuyến qua $I$ và cắt $DC$ kéo dài tại $M$ thì \(\widehat {CIM} = {30^0}\). Số đo góc $AOI$ là:
-
A
${120^0}$
-
B
${90^0}$
-
C
${60^0}$
-
D
${30^0}$
Đáp án của giáo viên lời giải hay : D
Tính \(\widehat {IOC} \Rightarrow \widehat {IOA}\) .
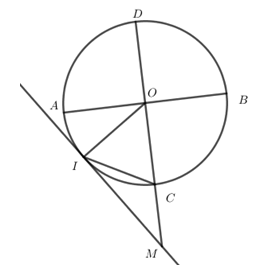
Ta có: \(\widehat {CIM}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung $IC$
\(\widehat {IOC}\) là góc ở tâm chắn cung $IC$
\(\begin{array}{l} \Rightarrow \widehat {CIM} = \dfrac{1}{2}\widehat {IOC} \Rightarrow \widehat {IOC} = 2\widehat {CIM} = {2.30^0} = {60^0}\\ \Rightarrow \widehat {IOA} = {90^0} - {60^0} = {30^0}\end{array}\)
Cho đường tròn $\left( {O;R} \right)$ có hai đường kính $AB$ và $CD$ vuông góc. Gọi $I$ là điểm trên cung $AC$ sao cho khi vẽ tiếp tuyến qua $I$ và cắt $DC$ kéo dài tại $M$ thì $IC = CM$. Độ dài $OM$ tính theo bán kính là:
-
A
\(3R\)
-
B
$2R$
-
C
$\dfrac{3}{2}R$
-
D
$\dfrac{3}{4}R$
Đáp án của giáo viên lời giải hay : B
Chứng minh \(\Delta OIC\) đều, từ đó suy ra độ dài \(OM\).
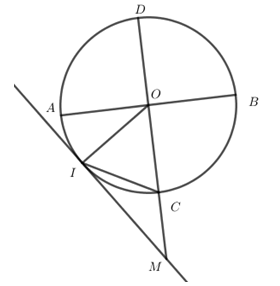
+) Ta có: \(\widehat {CIM} = \dfrac{1}{2}\widehat {IOC}\) (góc tạo bởi tiếp tuyến và dây cung với góc ở tâm chắn cung $IC$)
\( \Rightarrow \widehat {IOC} = 2\widehat {CIM}\).
Lại có \(\widehat {OCI} = \widehat {CIM} + \widehat {CMI} = 2\widehat {CIM}\) (do \(\Delta CMI\) cân tại \(C\))
Do đó \(\Delta OIC\) đều (vì \(\widehat {OIC}=\widehat {IOC}=\widehat {OCI}\)) \( \Rightarrow \widehat {IOM} = {60^0}\).
+) Xét \(\Delta OIM\) vuông tại \(I\) có:
\(\cos \widehat {IOM} = \dfrac{{OI}}{{OM}} = \dfrac{R}{{OM}} = \dfrac{1}{2} \Rightarrow OM = 2R\).
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A$ và $B$. Một đường thẳng tiếp xúc với $\left( O \right)$ tại $C$, và tiếp xúc với đường tròn $\left( {O'} \right)$ tại $D$ sao cho tia \(AB\) cắt đoạn \(CD\). Vẽ đường tròn $\left( I \right)$ đi qua ba điểm $A,C,D$ cắt đường thẳng $AB$ tại một điểm thứ hai là $E$. Chọn câu đúng:
-
A
Tứ giác $BCED$ là hình thoi
-
B
Tứ giác $BCED$ là hình bình hành
-
C
Tứ giác $BCED$ là hình vuông
-
D
Tứ giác $BCED$ là hình chữ nhật
Đáp án của giáo viên lời giải hay : B
Sử dụng các tính chất: góc nội tiếp cùng chắn một cung; góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung.
Sử dụng dấu hiệu nhận biết một hình là hình bình hành, hình thoi, hình chữ nhật, hình vuông.
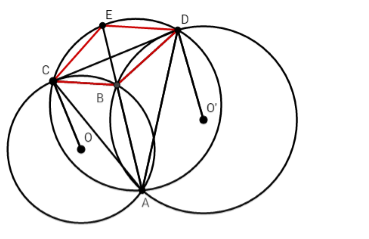
+) Xét $\left( O \right)$ ta có:
\(\widehat {BAC} = \widehat {BCD}\) (cùng chắn cung $CB$)
Xét $\left( I \right)$ có:
\(\widehat {CAB} = \widehat {EDC}\) (cùng chắn cung \(CE\))
\( \Rightarrow \widehat {BCD} = \widehat {EDC} \Rightarrow ED//BC\left( 1 \right)\)
+) Xét $\left( {O'} \right)$ có:
\(\widehat {BAD} = \widehat {BDC}\) (cùng chắn cung $BD$)
Xét $\left( I \right)$ có:
\(\widehat {EAD} = \widehat {ECD}\) (cùng chắn cung $ED$)
\( \Rightarrow \widehat {ECD} = \widehat {BDC} \Rightarrow CE//BD\left( 2 \right)\)
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $BDEC$ là hình bình hành
