Đường tròn ngoại tiếp đa giác là đường tròn
-
A
Tiếp xúc với tất cả các cạnh của đa giác đó
-
B
Đi qua tất cả các đỉnh của đa giác đó
-
C
Cắt tất cả các cạnh của đa giác đó
-
D
Đi qua tâm của đa giác đó
Đáp án của giáo viên lời giải hay : B
Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác .
Số đường tròn nội tiếp của một đa giác đều là
-
A
\(1\)
-
B
\(2\)
-
C
\(3\)
-
D
\(0\)
Đáp án của giáo viên lời giải hay : A
Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
Đường tròn nội tiếp hình vuông cạnh \(a\) có bán kính là
-
A
\(a\sqrt 2 \)
-
B
\(\dfrac{{a\sqrt 2 }}{2}\)
-
C
\(\dfrac{a}{2}\)
-
D
\(\dfrac{{a\sqrt 3 }}{2}\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng tính chất của hình vuông
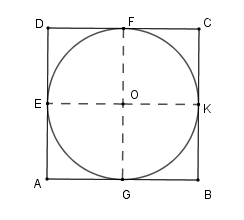
Gọi \(O\) là tâm của hình vuông \(ABCD\) , \(E;\,F;K;\,G\) là trung điểm của \(AD,\,DC,\,BC,\,AB\)
Khi đó ta có \(OE = OF = OK = OG = \dfrac{a}{2}\) . Hay \(O\) là tâm đường tròn nội tiếp hình vuông \(ABCD\) .
Bán kính đường tròn là \(R = \dfrac{a}{2}\) .
Cho lục giác đều \(ABCDEF\) nội tiếp đường tròn tâm \(O\) . Tính số đo góc \(AOB\) .
-
A
\(60^\circ \)
-
B
\(120^\circ \)
-
C
\(30^\circ \)
-
D
\(240^\circ \)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng tính chất lục giác đều
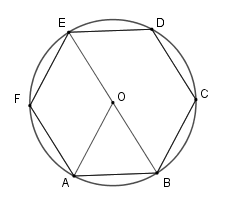
Ta có \(AB = BC = CD = DE = EF = FA\) nên số đo cung \(AB = \dfrac{1}{6}\) số đo cả đường tròn
Hay \(\widehat {AOB} = \dfrac{{360^\circ }}{6} = 60^\circ \) .
Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính \(4\,cm\) (làm tròn đến chữ số thập phân thứ nhất)
-
A
\(4,702\,cm\)
-
B
\(4,7\,cm\)
-
C
\(4,6\,cm\)
-
D
\(4,72\,cm\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng tính mối quan hệ giữa cung và dây cung để tính góc \(AOB\)
+ Sử dụng hệ thức giữa cạnh và góc trong tam giác.
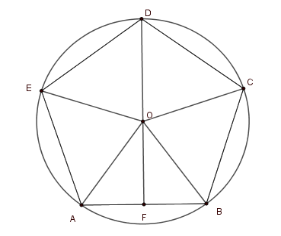
+ Vì \(AB = BC = CD = DE = EA\) nên các cung \(AB,BC,CD,DE,EA\) bằng nhau
Suy ra \(\widehat {AOB} = \dfrac{1}{5}.360^\circ = 72^\circ \)
+) Xét tam giác \(AOB\) cân tại \(O\) có \(OF\) là đường cao cũng là đường phân giác nên \(\widehat {BOF} = 36^\circ \)
Ta có \(FB = OB.\sin \widehat {BOF} = 4.\sin 36^\circ \Rightarrow AB = 2FB = 8\sin 36^\circ \approx 4,7\,cm\)
Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính \(4\,cm\) (làm tròn đến chữ số thập phân thứ nhất).
-
A
\(5,8\,cm\)
-
B
\(5,81\,cm\)
-
C
\(11,01\,cm\)
-
D
\(11,0\,cm\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng tính chất ngũ giác đều để tính góc \(AOB\)
+ Sử dụng hệ thức giữa cạnh và góc trong tam giác.

Gọi \(O\) là tâm đường tròn nội tiếp ngũ giác đều \(ABCDE\), đường cao \(OF \bot AB.\)
Khi đó bán kính của \(\left( O \right)\) là \(OF = 4\,cm\) .
Ta có \(\widehat {AOB} = \dfrac{{360^\circ }}{5} = 72^\circ \) \( \Rightarrow \widehat {BOF} = 36^\circ \)
Xét tam giác \(OFB\) có \(FB = OF.\tan 36^\circ = 4.\tan 36^\circ \Rightarrow AB = 8.\tan 36^\circ \approx 5,8 \,cm.\)
Tính cạnh của hình vuông nội tiếp \(\left( {O;R} \right)\)
-
A
\(\dfrac{R}{{\sqrt 2 }}\)
-
B
\(2R\)
-
C
\(\sqrt 2 R\)
-
D
\(2\sqrt 2 R\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng tính chất hình vuông để tìm bán kính đường tròn
+ Sử dụng định lý Pytago để tìm cạnh của hình vuông
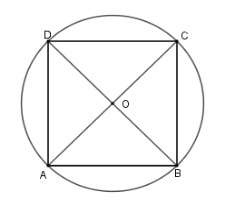
Gọi \(ABCD\) làhình vuông cạnh \(a\) nội tiếp đường tròn \(\left( O \right)\) suy ra $O$ là giao điểm hai đường chéo \(AC\) và \(BD\)
Từ đó \(R = OA = \dfrac{{AC}}{2} \Rightarrow AC = 2R\)
Theo định lý Pytago ta có \(A{B^2} + B{C^2} = A{C^2} \Rightarrow A{C^2} = {a^2} + {a^2} \Leftrightarrow A{C^2} = 2{a^2}\)
\( \Rightarrow AC = a\sqrt 2 = 2R \Rightarrow a = \sqrt 2 R\).
Tính độ dài cạnh của tam giác đều nội tiếp \(\left( {O;R} \right)\) theo \(R.\)
-
A
\(\dfrac{R}{{\sqrt 3 }}\)
-
B
\(\sqrt 3 R\)
-
C
\(R\sqrt 6 \)
-
D
\(3R\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng tính chất tam giác đều để tìm bán kính đường tròn
+ Sử dụng định lý Pytago để tìm cạnh của tam giác đều
+ Sử dụng công thức tính diện tích tam giác \(S = \dfrac{{ah}}{2}\) với \(h\) là chiều cao ứng với cạnh đáy là \(a\) .
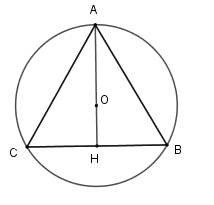
+ Gọi tam giác \(ABC\) đều cạnh \(a\) nội tiếp đường tròn \(\left( {O;R} \right)\) .
Khi đó \(O\) là trọng tâm tam giác \(ABC\) . Gọi \(AH\) là đường trung tuyến \( \Rightarrow R = AO = \dfrac{2}{3}AH \Rightarrow AH = \dfrac{{3R}}{2}\)
+ Theo định lý Pytago ta có \(A{H^2} = A{B^2} - B{H^2} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\)
Từ đó ta có \(\dfrac{{3R}}{2} = \dfrac{{a\sqrt 3 }}{2} \Rightarrow a = \sqrt 3 R\)
Cho \(\left( {O;4} \right)\) có dây \(AC\) bằng cạnh hình vuông nội tiếp và dây \(BC\) bằng cạnh tam giác đều nội tiếp đường tròn đó ( điểm \(C\) và \(A\) nằm cùng phía với \(BO\) ). Tính số đo góc \(ACB\)
-
A
\(30^\circ \)
-
B
\(45^\circ \)
-
C
\(60^\circ \)
-
D
\(15^\circ \)
Đáp án của giáo viên lời giải hay : D
+ Tìm số đo các cung \(BC\) và \(AB\) để tìm số đo cung \(AC\)
+ Sử dụng: số đo góc nội tiếp bằng nửa số đo cung bị chắn
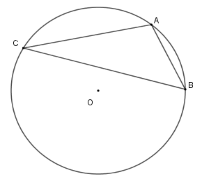
+ Vì \(AC\) bằng cạnh của hình vuông nội tiếp \(\left( O \right)\) nên số đo cung \(AC = 90^\circ \)
Vì \(BC\) bằng cạnh của tam giác đều nội tiếp \(\left( O \right)\) nên số đo cung \(BC = 120^\circ \)
Từ đó suy ra số đo cung \(AB = 120^\circ - 90^\circ = 30^\circ \)
+ Vì \(\widehat {ACB}\) là góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \dfrac{{30^\circ }}{2} = 15^\circ \)
Cho ngũ giác đều \(ABCDE\). Gọi \(K\) là giao điểm của \(AC\) và \(BE\) . Khi đó hệ thức nào dưới đây là đúng?
-
A
\(C{B^2} = AK.AC\)
-
B
\(O{B^2} = AK.AC\)
-
C
\(AB + BC = AC\)
-
D
Cả A, B, C đều sai.
Đáp án của giáo viên lời giải hay : A
Sử dụng tam giác đồng dạng
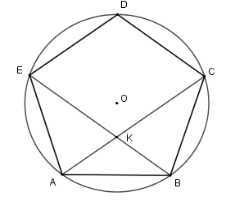
Vì \(AB = AE\) (do \(ABCDE\) là ngũ giác đều ) nên cung \(AB = \) cung \(AE\)
Xét tam giác \(AKB\) và tam giác \(ABC\) có
\(\widehat A\) chung và \(\widehat {KBA} = \widehat {KCB}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB,AE\) )
Suy ra \(\Delta AKB\backsim\Delta ABC\left( {g - g} \right)\)
\(\Rightarrow \dfrac{{AK}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow A{B^2} = AK.AC\) .
Mà $AB = BC$ nên \(B{C^2} = AK.AC\) .
Theo bất đẳng thức tam giác thì \(AB + BC > AC\) nên C sai
Vì \(ABCDE\) là ngũ giác đều nên \(BC \ne OB\) nên B sai.
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số $\dfrac{R}{r}$ là:
-
A
$\dfrac{1}{{\sqrt 2 }}$
-
B
$2$
-
C
$\dfrac{{\sqrt 3 }}{2}$
-
D
đáp án khác
Đáp án của giáo viên lời giải hay : D
Chứng minh bán kính đường tròn ngoại tiếp và nội tiếp hình vuông là cạnh huyền và cạnh góc vuông của một tam giác vuông cân, từ đó suy ra tỉ lệ
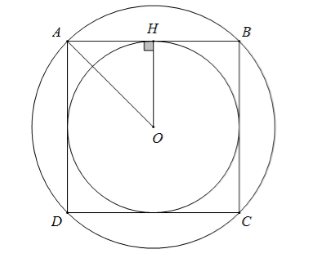
Giả sử hình vuông ABCD nội tiếp đường tròn (O)
⇒ O cũng là tâm đường tròn nội tiếp hình vuông
Gọi H là trung điểm AB ⇒ OH ⊥ AB tại H
Ta có R = OA, r = OH
Vì AO là phân giác của góc BAD nên
$\widehat {HAO} = \dfrac{{\widehat {BAD}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ $
Xét tam giác AHO vuông tại H có $ \sin \widehat {HAO} = \dfrac{{OH}}{{OA}}$$ \Leftrightarrow \dfrac{{OH}}{{OA}} = \sin {45^0} = \dfrac{1}{{\sqrt 2 }} $$\Leftrightarrow \dfrac{{OA}}{{OH}} = \sqrt 2 $ hay \(\dfrac{R}{r} = \sqrt 2 .\)
Bát giác đều ABCDEFGH nội tiếp đường tròn bán kính bằng 1. Tính độ dài cạnh AB của bát giác.
-
A
$2 - \sqrt 2 $
-
B
$2 + \sqrt 2 $
-
C
$\sqrt {2 - \sqrt 2 } $
-
D
Đáp án khác
Đáp án của giáo viên lời giải hay : C
Gọi O là tâm đường tròn ngoại tiếp bát giác đều
Vẽ BH ⊥ AO tại H
Tính BH, OH, AH
Sử dụng hệ thức lượng trong tam giác vuông $AB^2 = AH.AE$ để tính AB
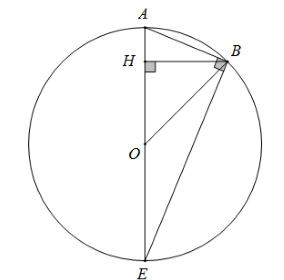
Vì ABCDEFGH là bát giác đều nên góc AOB bằng \(\dfrac{{360^\circ }}{8} = 45^\circ \) và AE là đường kính của đường tròn (O) ngoại tiếp bát giác.
Vẽ BH ⊥ AO tại H thì tam giác BHO vuông cân tại H (vì có góc BOH bằng \(45^0\).
Theo định lý Pytago ta có \(B{H^2} + O{H^2} = O{B^2}\)\( \Leftrightarrow 2B{H^2} = O{B^2} \)\(\Leftrightarrow BH = \dfrac{{OB}}{{\sqrt 2 }}\)
Suy ra
$\begin{array}{l}BH = OH = \dfrac{{OB}}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}\\AH = AO - OH = 1 - \dfrac{1}{{\sqrt 2 }}\\AE = 2AO = 2\end{array}$
Vì AE là đường kính của (O) nên ∆ ABE vuông tại B, áp dụng hệ thức lượng trong tam giác vuông ta có
$A{B^2} = AH.AE = \left( {1 - \dfrac{1}{{\sqrt 2 }}} \right).2 = 2 - \sqrt 2 $
$ \Rightarrow AB = \sqrt {2 - \sqrt 2 } $
