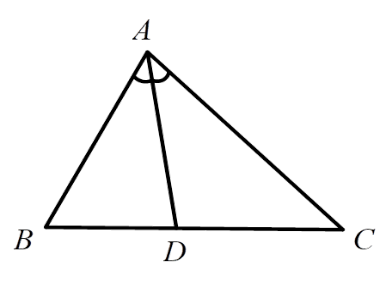
Cho \(\Delta ABC\), \(AD\) là phân giác trong của góc $A$ . Hãy chọn câu đúng:
-
A
\(\dfrac{{DC}}{{DB}} = \dfrac{{AB}}{{AC}}\)
-
B
\(\dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{DC}}\)
-
C
\(\dfrac{{AB}}{{DB}} = \dfrac{{DC}}{{AC}}\)
-
D
\(\dfrac{{AD}}{{DB}} = \dfrac{{AC}}{{AD}}\)
Đáp án của giáo viên lời giải hay : B
Sử dụng tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
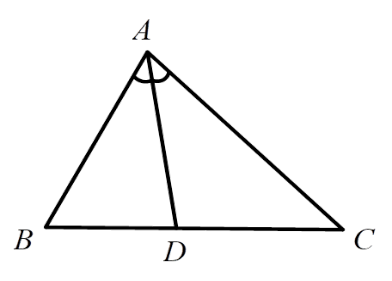
Vì \(AD\) là phân giác góc \(\widehat {BAC}\) nên ta có \(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}} \Leftrightarrow \dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{DC}}\) (tính chất đường phân giác của tam giác).
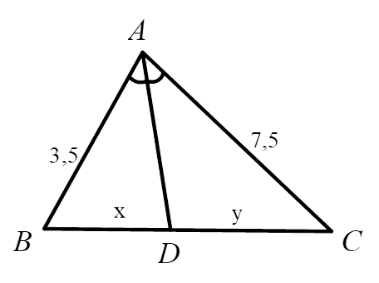
Hãy chọn câu đúng. Tỉ số \(\dfrac{x}{y}\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là $cm$ .
-
A
\(\dfrac{7}{{15}}\)
-
B
\(\dfrac{1}{7}\)
-
C
\(\dfrac{{15}}{7}\)
-
D
\(\dfrac{1}{{15}}\)
Đáp án của giáo viên lời giải hay : A
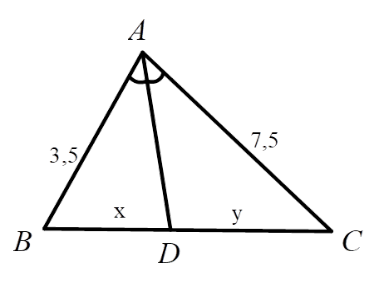
Xét tam giác \(ABC\), vì \(AD\) là phân giác góc \(\widehat {BAC}\) nên ta có \(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}} \Leftrightarrow \dfrac{x}{y} = \dfrac{{3,5}}{{7,5}} = \dfrac{7}{{15}}\)
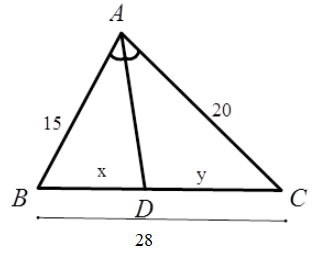
Hãy chọn câu đúng. Tính độ dài \(x,y\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình có cùng đơn vị đo là $cm$ .
-
A
\(x = 16cm;\,y = 12cm\).
-
B
\(x = 14cm;\,y = 14cm\).
-
C
\(x = 14,3cm;\,y = 10,7cm\).
-
D
$x = 12\,cm;\,y = 16\,cm$.
Đáp án của giáo viên lời giải hay : D
Sử dụng tính chất đường phân giác của tam giác: "Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy."
Và sử dụng tính chất tỉ lệ thức.
Vì \(AD\) là phân giác \(\widehat {BAC}\) nên ta có
\(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}} = \dfrac{{15}}{{20}} = \dfrac{3}{4}\\ \Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{3}{4} \Rightarrow \dfrac{{BD}}{{BD + DC}} = \dfrac{3}{{4 + 3}} = \dfrac{3}{7}\\ \Leftrightarrow \dfrac{{BD}}{{BC}} = \dfrac{3}{7} \Rightarrow \dfrac{x}{{28}} = \dfrac{3}{7}\\ \Rightarrow x = 12\,cm\)\( \Rightarrow y = 28 - x = 16\,cm\)
Vậy $x = 12\,cm;\,y = 16\,cm$ .
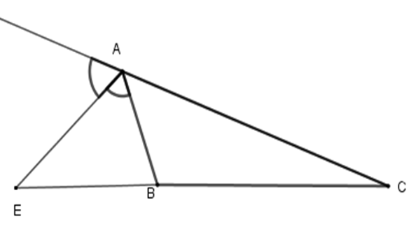
Cho \(\Delta ABC\), \(AE\) là phân giác ngoài của góc A. Hãy chọn câu đúng:
-
A
\(\dfrac{{AB}}{{AE}} = \dfrac{{BE}}{{CE}}\).
-
B
\(\dfrac{{AE}}{{AC}} = \dfrac{{BE}}{{CE}}\).
-
C
\(\dfrac{{AB}}{{AC}} = \dfrac{{CE}}{{BE}}\).
-
D
\(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\).
Đáp án của giáo viên lời giải hay : D
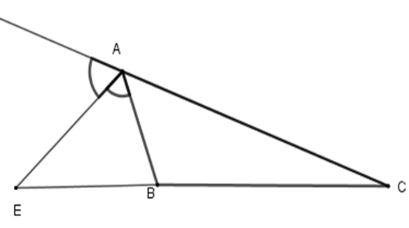
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hoai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên \(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\)
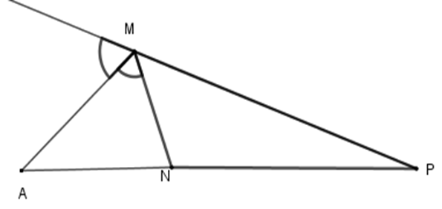
Cho \(\Delta MNP,MA\) là phân giác ngoài của góc $M$ , biết \(\dfrac{{NA}}{{PA}} = \dfrac{3}{4}\). Hãy chọn câu đúng.
-
A
\(\dfrac{{MN}}{{MP}} = 4\).
-
B
\(\dfrac{{MN}}{{MP}} = 3\).
-
C
\(\dfrac{{MN}}{{MP}} = \dfrac{1}{3}\).
-
D
\(\dfrac{{MN}}{{MP}} = \dfrac{3}{4}\).
Đáp án của giáo viên lời giải hay : D
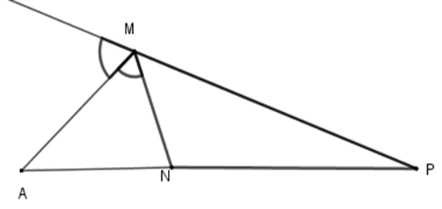
Theo tính chất đường phân giác của tam giác ta có \(\dfrac{{MN}}{{MP}} = \dfrac{{NA}}{{PA}} = \dfrac{3}{4}\)
Cho tam giác $ABC$ , $AC = 2AB$ , $AD$ là đường phân giác của tam giác $ABC$ , khi đó \(\dfrac{{BD}}{{CD}} = ?\)
-
A
\(\dfrac{{BD}}{{CD}} = 1\)
-
B
\(\dfrac{{BD}}{{CD}} = \dfrac{1}{3}\)
-
C
\(\dfrac{{BD}}{{CD}} = \dfrac{1}{4}\)
-
D
\(\dfrac{{BD}}{{CD}} = \dfrac{1}{2}\)
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất đường phân giác của tam giác để tìm ra tỉ lệ thức phù hợp, từ đó tìm ra kết quả của đề bài.
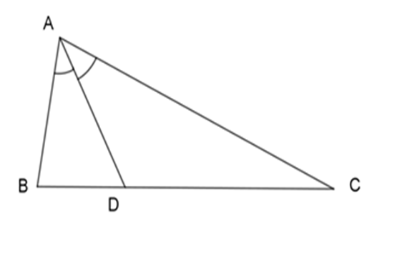
Vì $AD$ là phân giác của \(\Delta ABC\) nên: \(\dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{DC}}\)
Theo bài, ta có: $AC = 2AB$
\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{1}{2} \Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{1}{2}\)
Cho tam giác $ABC$ cân tại $A$ , đường phân giác trong của góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 15$ $cm$ , $BC = 10cm$ . Khi đó $AD = $ ?
-
A
3 cm
-
B
6cm
-
C
9 cm
-
D
12 cm
Đáp án của giáo viên lời giải hay : C
Kết hợp tính chất định lý, đã học và tính chất đường phân giác của tam giác để tìm ra tỉ lệ thức phù hợp, từ đó tìm ra độ dài $AD$ .
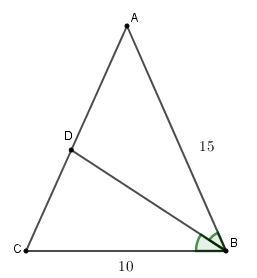
Vì $BD$ là đường phân giác của \(\widehat {ABC}\) nên:
\(\dfrac{{AD}}{{DC}} = \dfrac{{AB}}{{BC}}\)
Suy ra: \(\dfrac{{AD}}{{DC + AD}} = \dfrac{{AB}}{{BC + AB}}\)
(theo tính chất dãy tỉ số bằng nhau)
\( \Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{{AB}}{{BC + AB}}\)
Mà tam giác $ABC$ cân tại $A$ nên $AC = AB = 15cm.$\( \Rightarrow \dfrac{{AD}}{{15}} = \dfrac{{15}}{{15 + 10}} \)\(\Rightarrow AD = \dfrac{{15.15}}{{25}} = 9\;cm\)
Cho tam giác $ABC$ , \(\widehat A = {90^0}\), $AB = 15 cm, AC = 20 cm,$ đường cao $AH$ \((H \in BC)\). Tia phân giác của \(\widehat {HAB}\) cắt $HB$ tại $D$ . Tia phân giác của \(\widehat {HAC}\) cắt $HC$ tại $E$ . Tính $DH$ ?
-
A
$4cm$
-
B
$6cm$
-
C
$9cm$
-
D
$12cm$
Đáp án của giáo viên lời giải hay : A
Bước 1: Áp dụng các tính chất và định lý đã học để tìm ra dữ kiện cần thiết.
Bước 2: Áp dụng tính chất đường phân giác của tam giác để tìm ra giá trị của $DH$ .
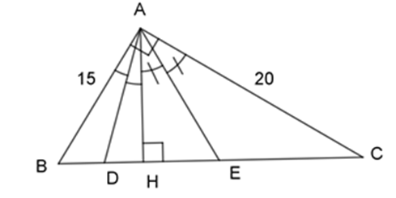
Áp dụng định lý Pytago vào tam giác $ABC$ vuông tại$A$ , ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {15^2} + {20^2} = B{C^2}\\ \Rightarrow BC = 25\end{array}\)
Ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}.AB.AC = \dfrac{1}{2}.AH.BC\)
\( \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{15.20}}{{25}} = 12\)
Áp dụng định lý Pitago trong tam giác $AHB$ vuông tại$H$ , ta có:
\(\begin{array}{l}\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2}\\ \Leftrightarrow {15^2} = {12^2} + H{B^2}\\ \Rightarrow H{B^2} = 81 \Rightarrow HB = 9\\ \Rightarrow HC = BC - HB = 25 - 9 = 16.\end{array}\)
Vì $AD$ là phân giác của tam giác $ABH$ nên:
\(\begin{array}{l}\dfrac{{AB}}{{AH}} = \dfrac{{BD}}{{DH}} \Leftrightarrow \dfrac{{AB}}{{AH}} = \dfrac{{BH - DH}}{{DH}}\\ \Leftrightarrow \dfrac{{15}}{{12}} = \dfrac{{9 - DH}}{{DH}} \Leftrightarrow 15DH = 108 - 12DH \Leftrightarrow DH = 4\,cm.\end{array}\)
Cho tam giác $ABC,AB = AC = 10cm,$$BC = 12cm.$ Gọi $I$ là giao điểm của các đường phân giác của tam giác $ABC.$ Tính $BI$ ?
-
A
$9\,cm$
-
B
$6\,cm$
-
C
$45\,cm$
-
D
$3\sqrt 5 \,cm$
Đáp án của giáo viên lời giải hay : D
- Áp dụng các tính chất, định lý đã học để tìm ra các dữ kiện cần thiết.
- Áp dụng tính chất đường phân giác của tam giác để tìm ra tỉ lệ thức phù hợp.
- Sử dụng dữ kiện và tỉ lệ thức vừa tìm được để tính $BI$ .
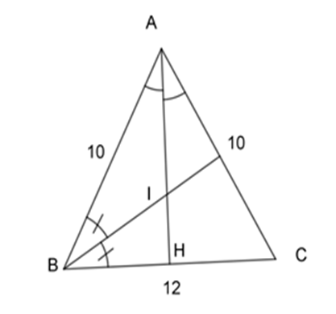
- Ta có $AB = AC = 10 cm$
Suy ra \(\Delta ABC\) cân tại A.
- Có I là giao các đường phân giác của \(\Delta ABC\).
Suy ra $AI, BI$ là đường phân giác của \(\Delta ABC\).
- Gọi $H$ là giao của $AI$ và $BC.$
- Khi đó ta có $AH$ vừa là đường phân giác, vừa là đường cao,
vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân $ABC$ (tính chất tam giác cân).
\( \Rightarrow \) $H$ là trung điểm của cạnh $BC$ \( \Rightarrow BH = HC = \dfrac{{BC}}{2} = \dfrac{{12}}{2} = 6\;cm\).
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,A{H^2} + B{H^2} = A{B^2}\\ \Leftrightarrow A{H^2} + {6^2} = {10^2}\\ \Leftrightarrow A{H^2} = 100 - 36 = 64\\ \Rightarrow AH = 8\end{array}\)
Vì $BI$ là phân giác của tam giác $ABH$ nên:
\(\begin{array}{l}\dfrac{{AB}}{{BH}} = \dfrac{{AI}}{{IH}} = \dfrac{{AH - IH}}{{IH}}\\ \Leftrightarrow \dfrac{{10}}{6} = \dfrac{{8 - IH}}{{IH}}\\ \Leftrightarrow 10IH = 48 - 6IH\\ \Leftrightarrow IH = 3\end{array}\)
Áp dụng định lý Pitago trong tam giác $BHI$ vuông tại $H,$ ta có:
$\begin{array}{l}\,\,\,\,\,\,\,\,B{I^2} = I{H^2} + B{H^2}\\ \Leftrightarrow B{I^2} = {3^2} + {6^2}\\ \Leftrightarrow B{I^2} = 45\\ \Rightarrow BI = 3\sqrt 5 \end{array}$
Cho tam giác $ABC$ có chu vi $18cm$ , các đường phân giác $BD$ và $CE$ . Tính các cạnh của tam giác $ABC$ , biết $\dfrac{{AD}}{{DC}} = \dfrac{1}{2},\dfrac{{AE}}{{EB}} = \dfrac{3}{4}$.
-
A
$AC = 4\,cm,BC = 8\,cm,AB = 6\,cm$
-
B
$AB = 4\,cm,BC = 6\,cm,AC = 8\,cm$
-
C
$AB = 4\,cm,BC = 8\,cm,AC = 6\,cm$
-
D
$AB = 8\,cm,BC = 4\,cm,AC = 6\,cm$
Đáp án của giáo viên lời giải hay : C
Bước 1: Sử dụng tính chất đường phân giác của tam giác.
Bước 2: Sử dụng tính chất tỉ lệ thức để biến đổi.
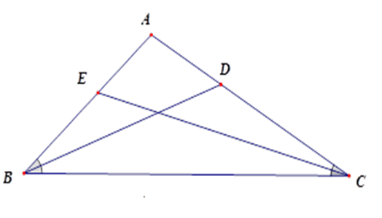
Theo tính chất đường phân giác, ta có
$\dfrac{{AB}}{{BC}} = \dfrac{{AD}}{{DC}} = \dfrac{1}{2},$
$\dfrac{{AC}}{{BC}} = \dfrac{{AE}}{{EB}} = \dfrac{3}{4}$nên
$\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3},$
Do đó $\dfrac{{AB}}{2} = \dfrac{{BC}}{4} = \dfrac{{AC}}{3} = \dfrac{{AB + BC + AC}}{{2 + 4 + 3}} = \dfrac{{18}}{9} = 2$.
Vậy $AB = 4\,cm,BC = 8\,cm,AC = 6\,cm.$
Cho tam giác $ABC$ , đường trung tuyến $AM$ . Tia phân giác của góc $AMB$ cắt $AB$ ở $D$ , tia phân giác của góc $AMC$ cắt $AC$ ở$E$ . Gọi $I$ là giao điểm của $AM$ và $DE$ .
Chọn khẳng định đúng.
-
A
\(DE{\rm{//}}BC\)
-
B
\(DI = IE\)
-
C
\(DI > IE\)
-
D
Cả A, B đều đúng.
Đáp án của giáo viên lời giải hay : D
+ Sử dụng tính chat đường phân giác của tam giác.
+ Sử dụng định lý Ta-lét và hệ quả của định lý Ta-lét.
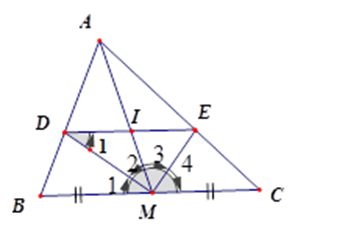
Vì \(MD\) và \(ME\) lần lượt là phân giác của \(\widehat {AMB};\,\widehat {AMC}\) nên \(\dfrac{{DA}}{{DB}} = \dfrac{{MA}}{{MB}},\dfrac{{EA}}{{EC}} = \dfrac{{MA}}{{MC}}\)
mà $MB = MC$ nên \(\dfrac{{DA}}{{DB}} = \dfrac{{EA}}{{EC}} \Rightarrow DE{\rm{//}}BC\)( định lí Ta-lét đảo).
Vì \(DE{\rm{//}}BC\) nên \(\dfrac{{DI}}{{BM}} = \dfrac{{AI}}{{AM}} = \dfrac{{IE}}{{MC}}\) (hệ quả định lý Ta-lét) mà $BM = MC$ nên $DI = IE$ .
Nên cả A, B đều đúng.
Tính độ dài $DE$ , biết $BC = 30cm,AM = 10cm$ .
-
A
$9\,cm$
-
B
$6\,cm$
-
C
$15\,cm$
-
D
$12\,cm$
Đáp án của giáo viên lời giải hay : D
- Sử dụng tính chất: Hai tia phân giác của hai góc kề bì thì vuông góc với nhau để suy ra các cạnh bằng nhau nhờ tính chất đường trung tuyến trong tam giác vuông.
- Sử dụng định lý Ta-lét để có các tỉ số thích hợp tính \(DE\) .
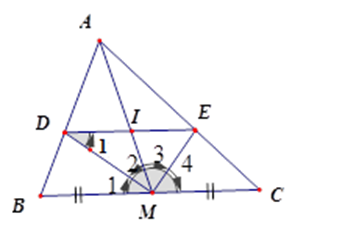
Vì $DI = IE$ (cmt) nên $MI$ là đường trung tuyến của tam giác $MDE$ .
\(\Delta MDE\) vuông ( vì $MD,ME$ là tia phân giác của góc kề bù) nên$MI = DI = IE$ .
Đặt$DI = MI = x$ , ta có $\dfrac{{DI}}{{BM}} = \dfrac{{AI}}{{AM}}$ (cmt) nên $\dfrac{x}{{15}} = \dfrac{{10 - x}}{{10}}.$ Từ đó x= 6 suy ra $DE = 12cm$ .
