Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
-
A
$4\,cm,5\,cm,6\,cm$ và$12\,cm,15\,cm,18\,cm$ .
-
B
$3\,cm,4\,cm,6\,cm$ và$9\,cm,12\,cm,18\,cm$ .
-
C
$1,5\,cm,2\,cm,2\,cm$ và$1\,cm,1\,cm,1\,cm$ .
-
D
$14\,cm,15\,cm,16\,cm$ và$7\,cm,7,5\,cm,8\,cm$ .
Đáp án của giáo viên lời giải hay : C
Sử dụng trường hợp đồng dạng thứ nhất: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
+ Sắp xếp các cạnh theo thứ tự từ nhỏ đến lớn và lập tỉ lệ. Từ đó suy ra hai tam giác đồng dạng.
Ta thấy $\dfrac{4}{{12}} = \dfrac{5}{{15}} = \dfrac{6}{{18}} = \dfrac{1}{3}$ ; \(\dfrac{3}{9} = \dfrac{4}{{12}} = \dfrac{6}{{18}} = \dfrac{1}{3}\) và \(\dfrac{{14}}{7} = \dfrac{{15}}{{7,5}} = \dfrac{{16}}{8} = 2\); \(\dfrac{{1,5}}{2} \ne \dfrac{2}{1} = \dfrac{2}{1}\) nên C sai.
Cho 2 tam giác RSK và PQM có \(\dfrac{{RS}}{{PQ}} = \dfrac{{RK}}{{PM}} = \dfrac{{SK}}{{QM}}\), khi đó ta có:
-
A
\(\Delta RSK\backsim\Delta PQM\)
-
B
\(\Delta RSK\backsim\Delta QPM\)
-
C
\(\Delta RSK\backsim\Delta MPQ\)
-
D
\(\Delta RSK\backsim\Delta QMP\)
Đáp án của giáo viên lời giải hay : A
Sử dụng cách chứng minh tam giác đồng dạng theo trường hợp thứ nhất cạnh – cạnh – cạnh để làm bài toán này.
2 tam giác RSK và PQM có \(\dfrac{{RS}}{{PQ}} = \dfrac{{RK}}{{PM}} = \dfrac{{SK}}{{QM}}\), khi đó ta có:\(\Delta RSK\;\; \backsim \;\;\Delta PQM\)
Cho \(\Delta ABC\) đồng dạng với \(\Delta MNP\). Biết \(AB = 5cm,BC = 6cm,MN = 10cm,MP = 5cm\). Hãy chọn câu đúng:
-
A
\(NP = 12cm,AC = 2,5cm\)
-
B
\(NP = 2,5cm,AC = 12cm\)
-
C
\(NP = 5cm,AC = 10cm\).
-
D
\(NP = 10cm,AC = 5cm\).
Đáp án của giáo viên lời giải hay : A
Sử dụng các cạnh tương ứng tỉ lệ của hai tam giác đồng dạng và giả thiết để tính các cạnh còn lại.
Vì \(\Delta ABC\) đồng dạng với \(\Delta MNP\) nên \(\dfrac{{AB}}{{MN}} = \dfrac{{AC}}{{MP}} = \dfrac{{BC}}{{NP}}\) hay
\(\begin{array}{l}\dfrac{5}{{10}} = \dfrac{{AC}}{5} = \dfrac{6}{{NP}}\\ \Rightarrow AC = \dfrac{{5.5}}{{10}} = 2,5;\,NP = \dfrac{{6.10}}{5} = 12\end{array}\)
Vậy \(NP = 12cm,AC = 2,5cm\).
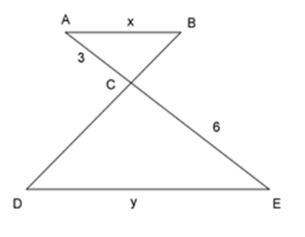
Cho tam giác \(\Delta ABC\backsim\Delta EDC\) như hình vẽ, tỉ số độ dài của $x$ và $y$ là:
-
A
$7 $
-
B
\(\dfrac{1}{2}\)
-
C
\(\dfrac{7}{4}\)
-
D
\(\dfrac{7}{{16}}\)
Đáp án của giáo viên lời giải hay : B
Áp dụng lý thuyết về tam giác đồng dạng, ta suy ra tỉ lệ thức phù hợp, từ đó tìm ra tỉ lệ $x$ và $y$ .
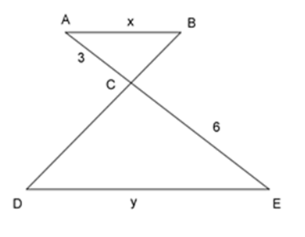
Ta có: \(\Delta ABC\backsim\Delta EDC\)
\( \Rightarrow \dfrac{{AB}}{{ED}} = \dfrac{{AC}}{{EC}} \Leftrightarrow \dfrac{x}{y} = \dfrac{3}{6} = \dfrac{1}{2}\)
\(\Delta ABC\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_1},\) \(\Delta MNP\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_2}.\) \(\Delta ABC\)\(\backsim\)$\Delta MNP$ theo tỉ số nào?
-
A
\({k_1}\).
-
B
\(\dfrac{{{k_2}}}{{{k_1}}}\)
-
C
\({k_1}{k_2}\)
-
D
\(\dfrac{{{k_1}}}{{{k_2}}}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng tỉ số đồng dạng của hai tam giác đồng dạng.
Vì \(\Delta ABC\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_1},\) \(\Delta MNP\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_2}\) nên ta có \(\dfrac{{AB}}{{DE}} = {k_1} \Rightarrow AB = {k_1}.DE\) và \(\dfrac{{MN}}{{DE}} = {k_2} \Rightarrow MN = {k_2}.DE\).
Từ đó ta có \(\dfrac{{AB}}{{MN}} = \dfrac{{{k_1}.DE}}{{{k_2}.DE}} = \dfrac{{{k_1}}}{{{k_2}}}.\)
Cho \(\Delta ABC\)\(\backsim\)\(\Delta IKH\). Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) \(\dfrac{{HI}}{{AC}} = \dfrac{{KH}}{{BC}} = \dfrac{{KI}}{{AB}};\)
(II) \(\dfrac{{AB}}{{IK}} = \dfrac{{AC}}{{HI}} = \dfrac{{BC}}{{KH}};\)
(III) \(\dfrac{{AC}}{{IH}} = \dfrac{{AB}}{{KI}} = \dfrac{{BC}}{{IK}}.\)
-
A
\(0\).
-
B
\(1\)
-
C
\(2\)
-
D
\(3\)
Đáp án của giáo viên lời giải hay : C
Sử dụng các cạnh tương ứng tỉ lệ của các tam giác đồng dạng.
Vì \(\Delta ABC\)\(\backsim\)\(\Delta IKH\) nên \(\dfrac{{AB}}{{IK}} = \dfrac{{BC}}{{KH}} = \dfrac{{AC}}{{IH}}\) hay \(\dfrac{{IK}}{{AB}} = \dfrac{{KH}}{{BC}} = \dfrac{{IH}}{{AC}}\) nên (I) và (II) đúng, (III) sai.
Tứ giác $ABCD$ có $AB = 8\,cm,BC = 15\,cm,CD = 18\,cm,AD = 10\,cm,BD = 12\,cm.$
Chọn câu đúng nhất:
-
A
\(\Delta ABD\)\(\backsim\) \(\Delta BDC\).
-
B
$ABCD$ là hình thang.
-
C
$ABCD$ là hình thang vuông.
-
D
Cả A, B đều đúng.
Đáp án của giáo viên lời giải hay : D
+ Sử dụng cách chứng minh hai tam giác đồng dạng theo trường hợp cạnh-cạnh-cạnh.
+ Từ đó suy ra cặp góc tương ứng bằng nhau để chứng minh hai đường thẳng song song
+ Suy ra \(ABCD\) là hình thang.
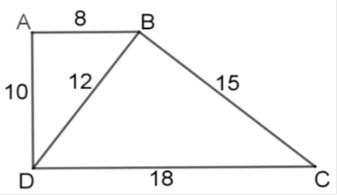
Ta có \(\dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{DC}}\) (vì \(\dfrac{8}{{12}} = \dfrac{{10}}{{15}} = \dfrac{{12}}{{18}}\,\left( { = \dfrac{2}{3}} \right)\) )
nên \(\Delta ABD\)\(\backsim\) \(\Delta BDC\,\left( {c - c - c} \right)\)
\(\Delta ABD\)\(\backsim\)\(\Delta BDC\)nên \(\widehat {ABD} = \widehat {BDC}.\) Mà hai góc này ở vị trí so le trong nên $AB$ //$CD$ . Vậy $ABCD$ là hình thang.
Lại có \(B{D^2} = 144 < 164 = A{D^2} + A{B^2}\) nên \(\Delta ABD\) không vuông. Do đó \(ABCD\) không là hình thang vuông.
Vậy A, B đều đúng, C sai.
Cho tam giác $ABC$ . Các điểm $D,E,F$ theo thứ tự là trung điểm của $BC,CA,AB$ . Các điểm $A',B',C'$ theo thứ tự là trung điểm của $EF,DF,DE$ . Chọn câu đúng?
-
A
\(\Delta A'B'C'\)\(\backsim\)\(\Delta ABC\) theo tỉ số \(k = \dfrac{1}{2}\)
-
B
\(\Delta EDF\)\(\backsim\)\(\Delta ABC\) theo tỉ số \(k = \dfrac{1}{2}\)
-
C
\(\Delta A'B'C'\)\(\backsim\)\(\Delta ABC\) theo tỉ số \(k = \dfrac{1}{4}\)
-
D
\(\Delta A'B'C'\)\(\backsim\)\(\Delta EDF\) theo tỉ số \(k = \dfrac{1}{2}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng tính chất đường trung bình của tam giác để suy ra tỉ số các cạnh từ đó có các tam giác đồng dạng.
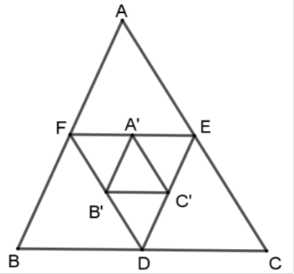
Vì $D,E,F$ theo thứ tự là trung điểm của $BC,CA,AB$ nên \(EF;\,ED;\,FD\) là các đường trung bình của tam giác \(ABC\) nên \(\dfrac{{EF}}{{BC}} = \dfrac{{FD}}{{AC}} = \dfrac{{ED}}{{AB}} = \dfrac{1}{2}\) suy ra \(\Delta ABC\backsim\Delta DEF\,\left( {c - c - c} \right)\) theo tỉ số đồng dạng \(k =2\) .
Tương tự ta có \(A'B';\,B'C';\,C'A'\) là các đường trung bình của tam giác \(DEF\) nên \(\Delta A'B'C'\)\(\backsim\)\(\Delta DEF\) theo tỉ số \(k = \dfrac{1}{2}\)
Theo tính chất đường trung bình $\dfrac{{B'C'}}{{EF}} = \dfrac{1}{2}$ mà $\dfrac{{EF}}{{BC}} = \dfrac{1}{2}$ (cmt) suy ra \(\dfrac{{B'C'}}{{BC}} = \dfrac{1}{4}.\)
Tương tự \(\dfrac{{A'B'}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{1}{4}.\)
Do đó \(\Delta A'B'C'\)\(\backsim\)\(\Delta ABC\,\left( {c - c - c} \right)\) theo tỉ số \(k = \dfrac{1}{4}\).
Cho \(\Delta ABC\) nhọn, kẻ đường cao $BD$ và $CE$ , vẽ các đường cao $DF$ và $EG$ của \(\Delta \;ADE\).
\(\Delta ABD\) đồng dạng với tam giác nào dưới đây?
-
A
$\Delta \;AEG$.
-
B
\(\Delta ABC\)
-
C
Cả A và B
-
D
Không có tam giác nào.
Đáp án của giáo viên lời giải hay : A
+ Áp dụng định lý Talet để tìm ra tỉ lệ thức của các cạnh tỉ lệ trong $2$ tam giác.
+ Từ đó suy ra 2 tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh.
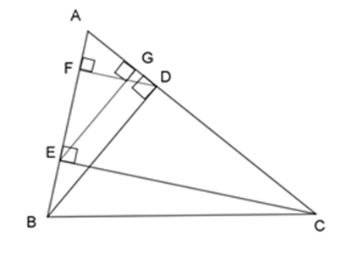
Xét \(\Delta ABD\) và $\Delta \;AEG$, ta có:
\(BD \bot AC\) ($BD$ là đường cao)
\(EG \bot AC\) ($EG$ là đường cao)
\( \Rightarrow BD{\rm{//}}EG\)
Theo định lý Talet, ta có:
\(\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}\)
\( \Rightarrow \)$\Delta AEG\backsim\Delta ABD$ (c - c -c) (điều phải chứng minh)
Chọn khẳng định đúng?
-
A
$AD.AE = AB.AF$.
-
B
$AD.AE = AB.AG = AC.AF$
-
C
$AD.AE = AC.GA$
-
D
$AD.AE = AB.AF = AC.AG$
Đáp án của giáo viên lời giải hay : B
Từ câu trước ta có $\Delta \;AEG\backsim\Delta ABD$ suy ra tỉ lệ cạnh, biến đổi thích hợp để tìm ra hệ thức đúng.
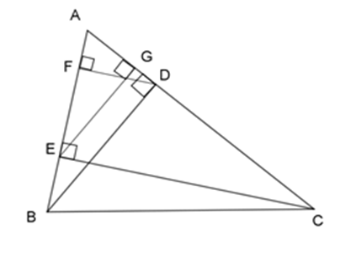
Từ câu trước ta có:
\(\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}}\)\( \Rightarrow AE.AD = AB.AG\;\;(1)\)
Chứng minh tương tự, ta được:
$\Delta AFD$$ \backsim $$\Delta AEC$ (c – c – c)
$ \Rightarrow \dfrac{{AF}}{{AE}} = \dfrac{{AD}}{{AC}} \Rightarrow AF.AC = AE.AD\;\;(2)$
Từ (1) và (2) ta có:
$AD.AE = AB.AG = AC.AF$ .
Một tam giác có cạnh nhỏ nhất bằng $8$ , hai cạnh còn lại bằng $x$ và $y$ \(\left( {x < y} \right).\) Một tam giác khác có cạnh lớn nhất bằng $27$ , hai cạnh còn lại cũng bằng $x$ và $y$ . Tính $x$ và $y$ để hai tam giác đó đồng dạng.
-
A
$x = 5;\,y = 10$.
-
B
$x = 6;\,y = 12$
-
C
$x = 12;\,y = 18$
-
D
$x = 6;\,y = 18$
Đáp án của giáo viên lời giải hay : C
+ Sắp xếp các cạnh của tam giác theo thứ tự tăng dần.
+ Lập tỉ lệ cạnh và tính $x,y$ .
Tam giác thứ nhất có các cạnh là \(8 < x < y\)
Tam giác thứ hai có các cạnh là $x < y < 27$ .
Vì hai tam giác đồng dạng nên \(\dfrac{8}{x} = \dfrac{x}{y} = \dfrac{y}{{27}}\) ta có \(x.y = 8.27\) và \({x^2} = 8y.\)
Do đó \({x^2} = 8y = 8 \cdot \dfrac{{8.27}}{x}\)nên \({x^3} = 64.27 = {\left( {4.3} \right)^3}.\)
Vậy \(x = 12,y = 18.\)
