Hãy chọn câu đúng. Nếu $\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì:
-
A
$\Delta ABC$ đồng dạng với $\Delta DEF$
-
B
$\Delta ABC$ đồng dạng với $\Delta EDF$
-
C
$\Delta BCA$ đồng dạng với $\Delta DEF$
-
D
$\Delta ABC$ đồng dạng với $\Delta FDE$
Đáp án của giáo viên lời giải hay : B
$\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì $\Delta ABC$ đồng dạng với $\Delta EDF$
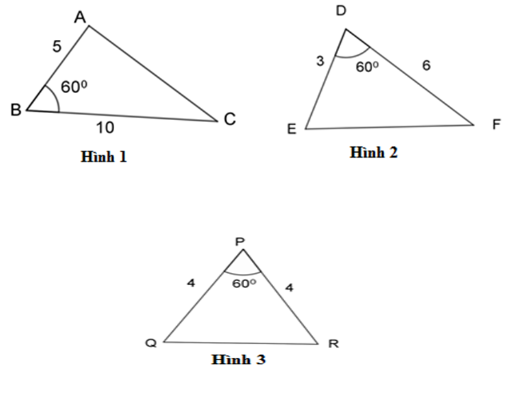
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
-
A
Hình 1 và hình 2
-
B
Hình 2 và hình 3
-
C
Hình 1 và hình 3
-
D
Tất cả đều đúng.
Đáp án của giáo viên lời giải hay : A
Bước 1: Xét tỉ số độ dài của các cặp cạnh từng tam giác.
Bước 2: Thấy cặp tam giác nào có tỉ số cặp cạnh của từng tam giác bằng nhau và góc xen giữa cặp cạnh đó bằng nhau thì cặp cạnh đang xét đồng dạng với nhau theo trường hợp cạnh – góc – cạnh.
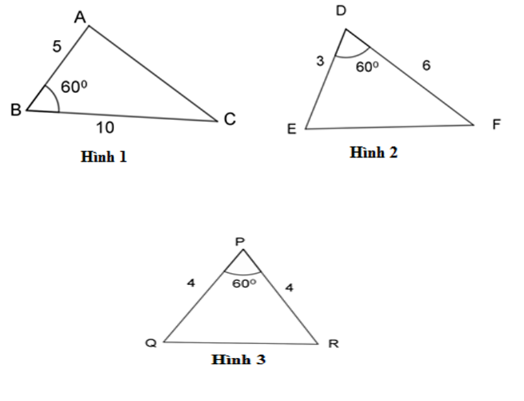
Có: \(\dfrac{{BA}}{{BC}} = \dfrac{5}{{10}} = \dfrac{1}{2},\;\dfrac{{DE}}{{DF}} = \dfrac{3}{6} = \dfrac{1}{2},\;\dfrac{{PQ}}{{PR}} = \dfrac{4}{4} = 1 \Rightarrow \dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}} = \dfrac{1}{2}.\)
Xét \(\Delta ABC\) và $\Delta EDF$ ta có:
$\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}\,\,\left( {cmt} \right) $$\Leftrightarrow \dfrac{{DE}}{{BA}} = \dfrac{{DF}}{{BC}}$
$\widehat B = \widehat D = {60^0}\;(gt)$
$\Rightarrow \Delta ABC\backsim \Delta EDF\,\,\,\left( {c - g - c} \right).$
Cho \(\Delta ABC\), lấy 2 điểm $D$ và $E$ lần lượt nằm bên cạnh $AB$ và $AC$ sao cho \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\). Kết luận nào sai?
-
A
\(\Delta \;ADE\backsim\Delta \;ABC\)
-
B
\(DE{\rm{//}}BC\)
-
C
\(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}}\)
-
D
\(\widehat {ADE} = \widehat {ABC}\)
Đáp án của giáo viên lời giải hay : C
Bước 1: Chứng minh cặp tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
Bước 2: Áp dụng định lý Talet đảo để tìm ra nhận định sai.
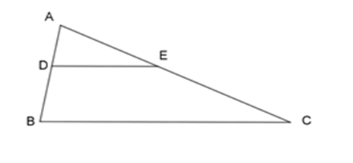
Xét $\Delta ADE$ và $\Delta ABC$ ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) (theo gt)
$\widehat A$ chung.
$ \Rightarrow \Delta ADE\backsim\Delta ABC$ (c – g – c)
$ \Rightarrow \widehat {ADE} = \widehat {ABC}$ (cặp góc tương ứng)
$ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}} \Rightarrow DE{\rm{//}}BC$ (định lý Talet đảo)
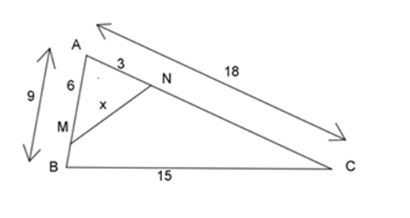
Cho hình vẽ dưới đây, tính giá trị của $x$ ?
-
A
\(x = 6\)
-
B
\(x = 5\)
-
C
\(x = 8\)
-
D
\(x = 9\)
Đáp án của giáo viên lời giải hay : B
Bước 1: Xét tỉ số độ dài của các cạnh tương ứng của 2 tam giác.
Bước 2: Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
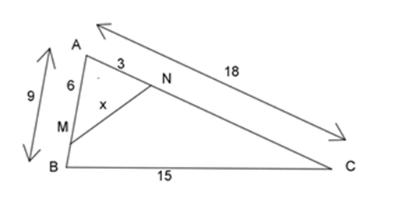
Ta có: \(\)
\(\dfrac{{AN}}{{AB}} = \dfrac{3}{9} = \dfrac{1}{3}\), \(\dfrac{{AM}}{{AC}} = \dfrac{6}{{18}} = \dfrac{1}{3}\)\( \Rightarrow \dfrac{{AN}}{{AB}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3}\)
Xét \(\Delta ANM\) và \(\Delta ABC\) có:
\(\dfrac{{AN}}{{AB}} = \dfrac{{AM}}{{AC}}\)(chứng minh trên)
\(\widehat A\;chung\)
\( \Rightarrow \Delta ANM\backsim\Delta ABC\) (c – g – c)
\(\begin{array}{l} \Rightarrow \dfrac{{AN}}{{AB}} = \dfrac{{AM}}{{AC}} = \dfrac{{MN}}{{CB}} = \dfrac{1}{3}\\ \Rightarrow \dfrac{x}{{15}} = \dfrac{1}{3} \Rightarrow x = \dfrac{{15}}{3} = 5\end{array}\)
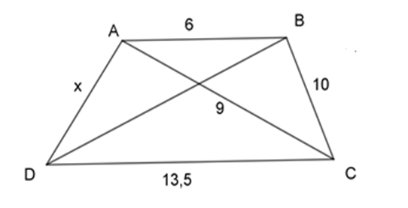
Với \(AB{\rm{//}}CD\) thì giá trị của \(x\) trong hình vẽ dưới đây là
-
A
\(x = 15\)
-
B
\(x = 16\)
-
C
\(x = 7\)
-
D
\(x = 8\)
Đáp án của giáo viên lời giải hay : A
- Xét tỉ số độ dài của các cạnh tương ứng của 2 tam giác.
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
- Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị của x.
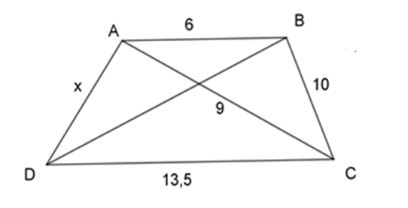
Ta có:
\(\dfrac{{AB}}{{AC}} = \dfrac{6}{9} = \dfrac{2}{3}\), \(\dfrac{{AC}}{{CD}} = \dfrac{9}{{13,5}} = \dfrac{2}{3}\) \( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{CD}} = \dfrac{2}{3}\)
Xét \(\Delta ABC\) và \(\Delta CAD\) có:
\(\dfrac{{AB}}{{AC}} = \dfrac{{AC}}{{CD}}\) (chứng minh trên)
\(\widehat {BAC} = \widehat {ACD}\) (cặp góc so le trong)
\( \Rightarrow \Delta ABC\backsim\Delta CAD\) (c – g – c)
\(\begin{array}{l} \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{CA}}{{CD}} = \dfrac{{BC}}{{AD}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{10}}{x} = \dfrac{2}{3} \Rightarrow x = \dfrac{{10.3}}{2} = 15\end{array}\)
Cho tam giác ABC có \(AB = 12cm,\;AC = 18cm,\;BC = 27cm.\) Điểm $D$ thuộc cạnh $BC$ sao cho
$CD = 12\,cm$ . Tính độ dài $AD$ .
-
A
$12\,cm$
-
B
$6\,cm$
-
C
$10\,cm$
-
D
$8\,cm$
Đáp án của giáo viên lời giải hay : D
Bước 1: Lập tỉ lệ cạnh để chứng minh \(\Delta ACB\) và \(\Delta DCA\) đồng dạng (cạnh-góc-cạnh)
Bước 2: Từ đó suy ra tỉ lệ cạnh còn lại để tính $AD$ .
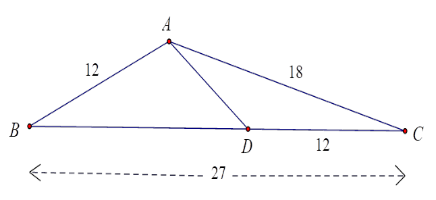
Ta có
\(\begin{array}{l}\dfrac{{AC}}{{DC}} = \dfrac{{18}}{{12}} = \dfrac{3}{2};\,\dfrac{{CB}}{{CA}} = \dfrac{{27}}{{18}} = \dfrac{3}{2}\\ \Rightarrow \dfrac{{CA}}{{CD}} = \dfrac{{CB}}{{CA}}\end{array}\)
Xét \(\Delta ACB\) và \(\Delta DCA\) có \(\widehat C\) chung và \(\dfrac{{CA}}{{CD}} = \dfrac{{CB}}{{CA}}\,\left( {cmt} \right)\)
Nên $\Delta ACB$ \(\backsim\) $\Delta DCA$ (c.g.c)
\(\begin{array}{l} \Rightarrow \dfrac{{AC}}{{DC}} = \dfrac{{AB}}{{DA}} \Leftrightarrow \dfrac{3}{2} = \dfrac{{12}}{{DA}}\\ \Rightarrow DA = \dfrac{{2.12}}{3} = 8\,cm\end{array}\)
Cho hình thang vuông $ABCD$ \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có $AB = 16\,cm,CD = 25\,cm,BD = 20\,cm$ .
Tam giác \(ABD\) đồng dạng với tam giác nào dưới đây?
-
A
$\Delta BDC$
-
B
$\Delta CBD$
-
C
$\Delta BCD$
-
D
$\Delta DCB$
Đáp án của giáo viên lời giải hay : A
- Xét tỉ số độ dài của các cạnh tương ứng của 2 tam giác.
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
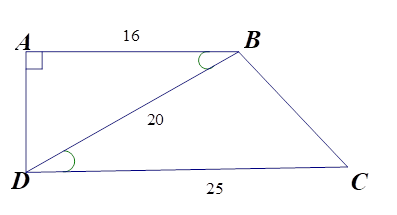
\(\Delta ABD\) và \(\Delta BDC\) có \(\widehat {ABD} = \widehat {BDC}\) (hai góc ở vị trí so le trong bằng nhau do\(AB{\rm{//CD}}\));
Và \(\dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}}\) (vì \(\dfrac{{16}}{{20}} = \dfrac{{20}}{{25}}\)).
Do đó \(\Delta ABD \backsim \Delta BDC\) (c.g.c).
Độ dài cạnh \(BC\) là
-
A
$10\,cm$
-
B
$12\,cm$
-
C
$15\,cm$
-
D
$9\,cm$
Đáp án của giáo viên lời giải hay : C
Từ \(\Delta ABD \backsim \Delta BDC\) ta suy ra \(\widehat {DBC}\) vuông nên áp dụng định lý Pytago để tính cạnh \(BC\) .
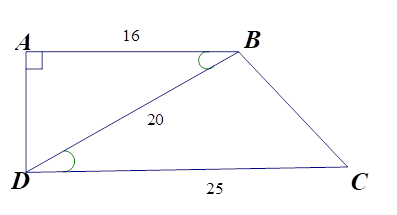
Vì \(\Delta ABD \backsim \Delta BDC\) (cmt) nên \(\widehat A = \widehat {DBC}\).
Ta có \(\widehat A = {90^0}\) nên \(\widehat {DBC} = {90^0}\). Theo định lí Py-ta-go, ta có
\(B{C^2} = C{D^2} - B{D^2} = {25^2} - {20^2} = {15^2}.\) Vậy \(BC = 15cm.\)
Cho tam giác ABC có \(AB = 8cm,\;AC = 16cm.\) Điểm $D$ thuộc cạnh $AB$ sao cho
$BD = 2cm$ . Điểm $E$ thuộc cạnh $AC$ sao cho $CE = 13cm$ .
Chọn câu đúng.
-
A
\(\Delta EDA \backsim \Delta ABC\)
-
B
\(\Delta ADE \backsim \Delta ABC\)
-
C
\(\Delta AED \backsim \Delta ABC\)
-
D
\(\Delta DEA \backsim \Delta ABC\)
Đáp án của giáo viên lời giải hay : C
- Xét tỉ số độ dài của các cạnh tương ứng của 2 tam giác.
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
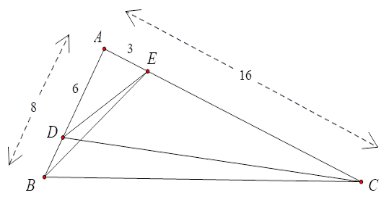
Ta có
\(\begin{array}{l}\dfrac{{AE}}{{AB}} = \dfrac{3}{8};\,\dfrac{{AD}}{{AC}} = \dfrac{6}{{16}} = \dfrac{3}{8}\\ \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}}\end{array}\)
Xét \(\Delta AED\) và \(\Delta ABC\) có \(\widehat A\) chung và \(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}}\,\left( {cmt} \right)\)
Nên \(\Delta AED\)\(\backsim\)\(\Delta ABC\) (c.g.c)
Chọn câu sai.
-
A
\(\widehat {ABE} = \widehat {ACD}\)
-
B
\(AE.CD = AD.BC\)
-
C
\(AE.CD = AD.BE\)
-
D
\(AE.AC = AD.AB\)
Đáp án của giáo viên lời giải hay : B
Bước 1: Chứng minh \(\Delta {\rm A}{\rm B}{\rm E}\backsim\Delta ACD\) (cạnh-góc-cạnh) từ đó suy ra cặp góc bằng nhau và hệ thức giữa các cạnh.
Bước 2: Từ \(\Delta AED\)\(\backsim\)\(\Delta ABC\) suy ra tỉ lệ cạnh từ đó có hệ thức đúng giữa các cạnh.
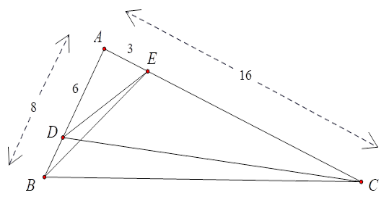
+ Xét \(\Delta ABE\) và \(\Delta ACD\) có \(\widehat A\) chung và $\dfrac{{AE}}{{AD}} = \dfrac{{AB}}{{AC}}\left( { = \dfrac{1}{2}} \right)$ nên \(\Delta {\rm A}{\rm B}{\rm E}\backsim\Delta ACD\,\left( {c - g - c} \right)\) suy ra \(\widehat {ABE} = \widehat {ACD}\) (hai góc tương ứng) và \(\dfrac{{AE}}{{AD}} = \dfrac{{BE}}{{CD}} \Rightarrow AE.CD = AD.BE\) .
+ \(\Delta AED\)\(\backsim\)\(\Delta ABC\) (cmt) nên \(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}} \Leftrightarrow AE.AC = AB.AD\).
Nên A, C, D đúng, B sai.
Cho tam giác nhọn ABC có \(\widehat C = {40^0}\). Vẽ hình bình hành $ABCD$ . Gọi $AH,AK$ theo thứ tự là các đường cao của các tam giác $ABC,ACD$ . Tính số đo $\widehat {AKH}$ .
-
A
\(30^\circ \)
-
B
\(40^\circ \)
-
C
\(45^\circ \)
-
D
\(50^\circ \)
Đáp án của giáo viên lời giải hay : B
Bước 1: Sử dụng công thức diện tích hình bình hành để suy ra hệ thức về cạnh. Sử dụng quan hệ từ vuông góc đến song song và mối quan hệ giữa các góc để suy ra hai góc bằng nhau.
Bước 2: Từ đó suy ra \(\Delta AKH\backsim\Delta ACB\) và tính được \(\widehat {AKH}\) .
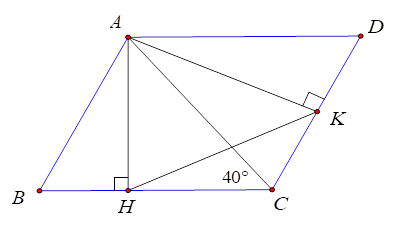
Vì $AD.AH = AB.AK$ \(( = {S_{ABCD}})\) nên \(\dfrac{{AH}}{{AK}} = \dfrac{{AB}}{{AD}} = \dfrac{{AB}}{{BC}}.\)
Ta lại có \(AB{\rm{//}}CD\,\)( vì $ABCD$ là hình bình hành) mà \(AK \bot DC \Rightarrow AK \bot AB \)\(\Rightarrow \widehat {BAK} = 90^\circ. \)
Từ đó \(\widehat {HAK} = \widehat {ABC}\) (cùng phụ với \(\widehat {BAH}\) )
Nên \(\Delta AKH\backsim\Delta BCA\)(c.g.c) \( \Rightarrow \widehat {AKH} = \widehat {ACB} = 40^\circ \) .
Cho tam giác $ABC$ có $AB = 9\,cm,AC = 16\,cm,BC = 20\,cm$ . Khi đó
-
A
\(\widehat B = \widehat {\dfrac{A}{3}}\)
-
B
\(\widehat B = \dfrac{2}{3}\widehat A\)
-
C
\(\widehat B = \widehat {\dfrac{A}{2}}\)
-
D
\(\widehat B = \widehat C\)
Đáp án của giáo viên lời giải hay : C
+ Kẻ đường phân giác $AE$ của \(\widehat {BAC}\) sau đó sử dụng tính chất đường phân giác của tam giác để tính \(EC\) .
+ Chứng minh \(\Delta ACB \backsim \Delta ECA\) (c-g-c) suy ra mối quan hệ giữa các góc.
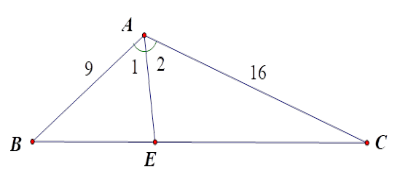
Kẻ đường phân giác $AE$ của \(\widehat {BAC}\) . Theo tính chất đường phân giác, ta có:
$\dfrac{{BE}}{{EC}} = \dfrac{{AB}}{{AC}} = \dfrac{9}{{16}}$ nên
$\dfrac{{BE + EC}}{{EC}} = \dfrac{{9 + 16}}{{16}}$ hay $\dfrac{{20}}{{EC}} = \dfrac{{25}}{{16}}.$
Suy ra $EC = 12,8\,cm$ .
Xét \(\Delta ACB\) và \(\Delta ECA\) có
\(\widehat C\) là góc chung;
$\dfrac{{AC}}{{CB}} = \dfrac{{EC}}{{CA}}$ (vì $\dfrac{{16}}{{20}} = \dfrac{{12,8}}{{16}}$).
Do đó \(\Delta ACB \backsim \Delta ECA\) (c.g.c) suy ra \(\widehat B = {\widehat A_2}\), tức là \(\widehat B = \widehat {\dfrac{A}{2}}\).
