Cho các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn
-
A
$5x + 7 < 0$
-
B
$0x + 6 > 0$
-
C
${x^2} - 2x > 0$
-
D
$x - 10 = 3$.
Đáp án của giáo viên lời giải hay : A
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn.
Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)) trong đó \(a\) và \(b\) là hai số đã cho, \(a \ne 0\), gọi là bất phương trình bậc nhất một ẩn.
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn ta có:
Đáp án A là bất phương trình bậc nhất một ẩn.
Đáp án B không phải bất phương trình bậc nhất một ẩn vì $a = 0.$
Đáp án C không phải bất phương trình bậc vì có \({x^2}.\)
Đáp án D không phải bất phương trình vì đây là phương trình bậc nhất một ẩn.
Giá trị $x = 2$ là nghiệm của bất phương trình nào sau đây ?
-
A
$7 - x < 2x$
-
B
$2x + 3 > 9$
-
C
$ - 4x \ge x + 5$
-
D
$5 - x > 6x - 12$
Đáp án của giáo viên lời giải hay : D
Có 2 cách làm:
Cách 1: Giải từng bất phương trình tìm nghiệm rồi xem $x = 2$ có thỏa mãn không?
Cách 2: Thay \(x = 2\) vào bất phương trình rồi so sánh hai vế của từng bất phương trình và kết luận
Trong bài này các em nên sử dụng cách thứ 2 để cho nhanh gọn hơn đỡ tốn thời gian làm bài.
(Trong bài này chúng ta làm theo cách thứ 2) thay \(x = 2\) vào từng bất phương trình:
Đáp án A: \(7 - 2 < 2.2 \Leftrightarrow 5 < 4\) vô lý. Loại đáp án A.
Đáp án B: \(2.2 + 3 > 9 \Leftrightarrow 7 > 9\) vô lý. Loại đáp án B.
Đáp án C: \( - 4.2 \ge 2 + 5 \Leftrightarrow - 8 \ge 7\) vô lý. Loại đáp án C.
Đáp án D: \(5 - 2 > 6.2 - 12 \Leftrightarrow 3 > 0\) luôn đúng. Chọn đáp án D.
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
-
A
$x > \dfrac{3}{5}$
-
B
$x \le - \dfrac{5}{3}$
-
C
$x \ge - \dfrac{5}{3}$
-
D
$x > - \dfrac{5}{3}$.
Đáp án của giáo viên lời giải hay : D
Giải bất phương trình tìm nghiệm phù hợp bằng cách dùng qui tắc nhân và qui tắc chuyển vế
Vì \(7 > 0\) nên \(7\left( {3x + 5} \right) \ge 3 \Leftrightarrow 3x + 5 > 0 \Leftrightarrow 3x > - 5 \Leftrightarrow x > - \dfrac{5}{3}.\)
Cho $a > b$. Bất đẳng thức nào tương đương với bất đẳng thức đã cho?
-
A
$a - 3 > b - 3$
-
B
$ - 3a + 4 > - 3b + 4$
-
C
$2a + 3 < 2b + 3$
-
D
$ - 5b - 1 < - 5a - 1$.
Đáp án của giáo viên lời giải hay : A
Áp dụng tính chất liên hệ giữa thứ tự và phép cộng, liên hệ giữa thứ tự và phép nhân.
+) Đáp án A: \(a > b \Leftrightarrow a - 3 > b - 3\)
Vậy ý A đúng chọn luôn ý A.
+) Đáp án B: \( - 3a + 4 > - 3b + 4 \Leftrightarrow - 3a > - 3b \Leftrightarrow a < b\) trái với giả thiết nên B sai.
+) Đáp án C: \(2a + 3 < 2b + 3 \Leftrightarrow 2a < 2b \Leftrightarrow a < b\) trái với giả thiết nên C sai.
+) Đáp án D: \( - 5b - 1 < - 5a - 1 \Leftrightarrow - 5b < - 5a \Leftrightarrow b > a\) trái với giả thiết nên D sai.
Phương trình \(\left| {2x - 5} \right| = 1\) có nghiệm là:
-
A
\(x = 3;x = 2\)
-
B
\(x = \dfrac{5}{2};x = 2\)
-
C
\(x = 1;x = 2\)
-
D
$x = 0,5{\rm{ }};x = 1,5$
Đáp án của giáo viên lời giải hay : A
Bỏ dấu giá trị tuyệt đối bằng công thức: \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\)
Giải phương trình: \(\left| {2x - 5} \right| = 1\)
$TH1:\;2x - 5 \ge 0 \Leftrightarrow x \ge \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = 2x - 5 = 1 \Leftrightarrow 2x = 6 \Leftrightarrow x = 3\;\;\left( {tm} \right)$
$TH2:\;2x - 5 < 0 \Leftrightarrow x < \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = - 2x + 5 = 1 \Leftrightarrow 2x = 4 \Leftrightarrow x = 2\;\;\left( {tm} \right)$
Vậy phương trình có hai nghiệm \(x = 3\) và \(\;x = 2\).
Phương trình \(\dfrac{1}{3} - \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{4}\) có nghiệm là
-
A
\(x = \dfrac{7}{{12}};x = \dfrac{1}{{12}}\)
-
B
\(x = \dfrac{8}{{12}};x = \dfrac{5}{{12}}\)
-
C
\(x = \dfrac{7}{{12}};x = \dfrac{2}{3}\)
-
D
\(x = \dfrac{1}{{12}};x = \dfrac{5}{{12}}\)
Đáp án của giáo viên lời giải hay : C
Bỏ dấu giá trị tuyệt đối bằng công thức: \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\)
\(\begin{array}{l}\;\;\;\;\;\dfrac{1}{3} - \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{4}\\ \Leftrightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{3} - \dfrac{1}{4}\\ \Leftrightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{{12}}\,\left( * \right)\end{array}\)
\(\begin{array}{l}TH1:\;\dfrac{5}{4} - 2x \ge 0 \Leftrightarrow x \le \dfrac{5}{8} \Rightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{5}{4} - 2x\\ \Rightarrow pt\,\,\left( * \right) \Leftrightarrow \dfrac{5}{4} - 2x = \dfrac{1}{{12}}\\ \Leftrightarrow 2x = \dfrac{7}{6}\\ \Leftrightarrow x = \dfrac{7}{{12}}\;\;\left( {tm} \right)\end{array}\)
\(\begin{array}{l}TH2:\;\;\dfrac{5}{4} - 2x < 0 \Leftrightarrow x > \dfrac{5}{8} \Rightarrow \left| {\dfrac{5}{4} - 2x} \right| = - \dfrac{5}{4} + 2x\;\\ \Rightarrow pt\,\left( * \right) \Leftrightarrow - \dfrac{5}{4} + 2x = \dfrac{1}{{12}}\\ \Leftrightarrow 2x = \dfrac{4}{3}\\ \Leftrightarrow x = \dfrac{2}{3}\;\;\left( {tm} \right).\;\end{array}\)
Vậy phương trình có hai nghiệm \(x = \dfrac{7}{{12}}\) và \(x = \dfrac{2}{3}\).
Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương trình nào?
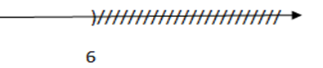
-
A
$x - 1 \ge 5$
-
B
$x + 1 \le 7$
-
C
$x + 3 < 9$
-
D
$x + 1 > 7$.
Đáp án của giáo viên lời giải hay : C
Tìm nghiệm của mỗi phương trình rồi so sánh với đề bài.
Theo đề bài thì trục số biểu diễn tập nghiệm \(x < 6.\)
Ta có
+) Đáp án A: $x - 1 \ge 5 \Leftrightarrow x \ge 6$ loại vì tập nghiệm là \(x < 6.\)
+) Đáp án B: \(x + 1 \le 7 \Leftrightarrow x \le 6\) loại vì tập nghiệm là \(x < 6.\)
+) Đáp án C: \(x + 3 < 9 \Leftrightarrow x < 6\) thỏa mãn vì tập nghiệm là \(x < 6.\)
+) Đáp án D: \(x + 1 > 7 \Leftrightarrow x > 6\) loại vì tập nghiệm là \(x < 6.\)
Với giá trị nào của $m$ thì bất phương trình $m(2x + 1) < 8$ là bất phương trình bậc nhất một ẩn?
-
A
$m \ne 1$
-
B
$m \ne - \dfrac{1}{3}$
-
C
$m \ne 0$
-
D
$m \ne 8$.
Đáp án của giáo viên lời giải hay : C
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn.
Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)) trong đó \(a\) và \(b\) là hai số đã cho, \(a \ne 0\), gọi là bất phương trình bậc nhất một ẩn.
Ta có: $m(2x + 1) < 8 \Leftrightarrow 2mx + m < 8 \Leftrightarrow 2mx + m - 8 < 0$.
Vậy để bất phương trình \(m\left( {2x + 1} \right) < 8\) là bất phương trình bậc nhất 1 ẩn thì \(2mx + m - 8 < 0\) là bất phương trình bậc nhất một ẩn.
Theo định nghĩa bất phương trình bậc nhất một ẩn thì \(a \ne 0\) hay \(2m \ne 0\) $\Leftrightarrow m \ne 0$
Tập nghiệm của bất phương trình $3x + 7 > x + 9$ là
-
A
$S = \left\{ {x|x > 1} \right\}$
-
B
$S = \left\{ {x|x > -1} \right\}$
-
C
$x = 1$
-
D
$S = \left\{ {x|x < 1} \right\}$
Đáp án của giáo viên lời giải hay : A
Áp dụng quy tắc chuyển vế để tìm nghiệm và biểu diễn trên trục số
\(3x + 7 > x + 9 \Leftrightarrow 3x - x > 9 - 7 \Leftrightarrow 2x > 2 \Leftrightarrow x >1\)
Vậy tập nghiệm của bất phương trình là $S = \left\{ {x|x > 1} \right\}$
Phương trình \(\left| {5x - 4} \right| = \left| {x + 2} \right|\) có nghiệm là
-
A
\(x = \dfrac{1}{3}\)
-
B
\(x = 1,5;x = \dfrac{{ - 1}}{3}\)
-
C
\(x = - 1,5;x = \dfrac{{ - 1}}{3}\)
-
D
\(x = 1,5;x = \dfrac{1}{3}\)
Đáp án của giáo viên lời giải hay : D
Vận dụng tính chất: \(\left| a \right| = \left| b \right| \Leftrightarrow \left[ \begin{array}{l}a = b\\a = - b\end{array} \right..\) Ta có: \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\)
$\begin{array}{l}\;\;\;\;\left| {5x - 4} \right| = \left| {x + 2} \right|\\ \Leftrightarrow \left[ \begin{array}{l}5x - 4 = x + 2\\5x - 4 = - x - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}4x = 6\\6x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{6}{4} = 1,5\\x = \dfrac{2}{6} = \dfrac{1}{3}\end{array} \right..\end{array}$
Tổng các nghiệm của phương trình \(7,5 - 3\left| {5 - 2x} \right| = - 4,5\) là
-
A
\(\dfrac{1}{2}\)
-
B
\(\dfrac{9}{2}\)
-
C
\(5\)
-
D
\(\dfrac{{11}}{2}\)
Đáp án của giáo viên lời giải hay : C
Dùng qui tắc chuyển vế biến đổi phương trình về dạng \(\left| A \right| = m\,\,\left( {m \ge 0} \right) \Leftrightarrow \left[ \begin{array}{l}A = m\\A = - m\end{array} \right.\)
\(\begin{array}{l}\;7,5 - 3\left| {5 - 2x} \right| = - 4,5\\ \Leftrightarrow 3\left| {5 - 2x} \right| = 7,5 + 4,5\\ \Leftrightarrow 3\left| {5 - 2x} \right| = 12\\ \Leftrightarrow \left| {5 - 2x} \right| = 4\\ \Leftrightarrow \left[ \begin{array}{l}5 - 2x = 4\\5 - 2x = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 1\\2x = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = \dfrac{9}{2}\end{array} \right..\end{array}\)
Vậy nghiệm của phương trình là \(x = \dfrac{1}{2};x = \dfrac{9}{2}\)
Nên tổng các nghiệm của phương trình là \(\dfrac{1}{2} + \dfrac{9}{2} = 5.\)
Số nghiệm của phương trình \(\left| {2x - 3} \right| - \left| {3x + 2} \right| = 0\) là
-
A
\(0\)
-
B
\(1\)
-
C
\(2\)
-
D
\(5\)
Đáp án của giáo viên lời giải hay : C
Vận dụng tính chất: \(\left| a \right| = \left| b \right| \Leftrightarrow \left[ \begin{array}{l}a = b\\a = - b\end{array} \right..\)
Từ đó ta có: \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\)
\(\begin{array}{l}\;\left| {2x - 3} \right| - \left| {3x + 2} \right| = 0\\ \Leftrightarrow \left| {2x - 3} \right| = \left| {3x + 2} \right|\\ \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 3x + 2\\2x - 3 = - (3x + 2)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 5\\5x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = \dfrac{1}{5}\end{array} \right..\end{array}\)
Vậy phương trình có hai nghiệm là \(x = - 5;x = \dfrac{1}{5}\)
Hình vẽ nào dưới đây biểu diễn tập nghiệm của bất phương trình $2x - 8 \le 13 - 5x.$
-
A
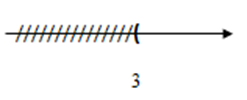
-
B
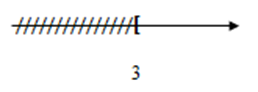
-
C
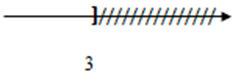
-
D
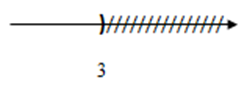
Đáp án của giáo viên lời giải hay : C
Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương
Cách biểu diễn nghiệm trên trục số
$2x - 8 \le 13 - 5x \Leftrightarrow 2x + 5x \le 13 + 8 \Leftrightarrow 7x \le 21 \Leftrightarrow x \le 21:7 \Leftrightarrow x \le 3$
Vậy tập nghiệm của phương trình \(S = \left\{ {x/x \le 3} \right\}\)
Biểu diễn tập nghiệm trên trục số
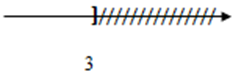
Nghiệm của phương trình \(\left| {x - 1} \right| = 3x - 2\) là:
-
A
\(x = \dfrac{3}{4}\)
-
B
\(x = \dfrac{1}{2};x = \dfrac{3}{4}\)
-
C
\(x = 1\)
-
D
Phương trình vô nghiệm
Đáp án của giáo viên lời giải hay : A
Xét phương trình \(\left| {A\left( x \right)} \right| = B\left( x \right)\;\;\;\left( 1 \right)\)
* Cách 1: Ta thấy nếu $B(x) < 0$ thì không có giá trị nào của x thoả mãn vì giá trị tuyệt đối của mọi số đều không âm.
Do vậy ta giải như sau: \(\left| {A\left( x \right)} \right| = B\left( x \right)\;\;\;\left( 1 \right)\)
Điều kiện: $B(x)$ \( \ge 0\) (*)
(1) Trở thành \(\left| {A\left( x \right)} \right| = B\left( x \right) \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\)
(Đối chiếu giá trị x tìm được với điều kiện (*))
* Cách 2: Chia khoảng xét điều kiện bỏ dấu giá trị tuyệt đối:
Nếu \(a \ge 0 \Rightarrow \left| a \right| = a.\)
Nếu \(a < 0 \Rightarrow \left| a \right| = - a.\)
Ta giải như sau: \(\left| {A\left( x \right)} \right| = B\left( x \right)\) (1)
Nếu $A(x)$ \( \ge 0\) thì (1) trở thành: $A\left( x \right) = B\left( x \right)$ (Đối chiếu giá trị $x$ tìm được với điều kiện).
Nếu $A (x ) < 0$ thì (1) trở thành: $ - {\rm{ }}A\left( x \right) = B\left( x \right)\;$ (Đối chiếu giá trị $x$ tìm được với điều kiện).
\(\left| {x - 1} \right| = 3x - 2\)
* Xét \(x - 1 \ge 0 \Leftrightarrow x \ge 1 \Rightarrow Pt \Leftrightarrow x - 1 = 3x - 2\)\( \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}\) (KTMĐK)
* Xét \(x - 1 < 0 \Leftrightarrow x < 1 \Rightarrow PT \Leftrightarrow - x + 1 = 3x - 2 \)\(\Leftrightarrow 4x = 3 \Leftrightarrow x = \dfrac{3}{4}\) (TMĐK)
Vậy phương trình có một nghiệm \(x = \dfrac{3}{4}\) .
Số nguyên lớn nhất thỏa mãn bất phương trình ${(x - 2)^2} - {x^2} - 8x + 3 \ge 0$ là
-
A
$x = 1$
-
B
$x = 0$
-
C
\(x = - 1\)
-
D
\(x \le \dfrac{7}{{12}}.\)
Đáp án của giáo viên lời giải hay : B
Phân tích hằng đẳng thức, biến đổi vế trái
Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương.
\(\begin{array}{l}{(x - 2)^2} - {x^2} - 8x + 3 \ge 0\\ \Leftrightarrow {x^2} - 4x + 4 - {x^2} - 8x + 3 \ge 0\\ \Leftrightarrow - 12x + 7 \ge 0\\ \Leftrightarrow x \le \dfrac{{ 7}}{{12}}\end{array}\)
Vậy nghiệm của bất phương trình là \(x \le \dfrac{7}{{12}}.\)
Nên số nguyên lớn nhất thỏa mãn bất phương trình là \(x = 0.\)
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
-
A
$x = - 3$
-
B
$x = 0$
-
C
\(x = - 1\)
-
D
\(x = - 2\).
Đáp án của giáo viên lời giải hay : D
Nhân đơn thức với đa thức
Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương.
\(\begin{array}{l}\;x(5x + 1) + 4(x + 3) > 5{x^2}\\ \Leftrightarrow 5{x^2} + x + 4x + 12 > 5{x^2}\\ \Leftrightarrow 5x > - 12\\ \Leftrightarrow x > \dfrac{{ - 12}}{5}\end{array}\)
Vậy nghiệm của bất phương trình là \(x > - \dfrac{{12}}{5}.\)
Số nguyên lớn nhất thỏa mãn bất phương trình là \(x = - 2.\)
Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có nghiệm là:
-
A
Vô nghiệm
-
B
$x \ge 4,11$
-
C
Vô số nghiệm
-
D
$x \le - 5$
Đáp án của giáo viên lời giải hay : D
- Áp dụng quy tắc chuyển vế
- Quy đồng bỏ mẫu
- Tìm $x$
Ta có:
$\begin{array}{l}\;\;\;\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x\\ \Leftrightarrow \dfrac{{3(3x + 5)}}{6} - \dfrac{6}{6} \le \dfrac{{2(x + 2)}}{6} + \dfrac{{6x}}{6}\\ \Leftrightarrow 3(3x + 5) - 6 \le 2(x + 2) + 6x\\ \Leftrightarrow 9x + 15 - 6 \le 2x + 4 + 6x\\ \Leftrightarrow 9x - 2x - 6x \le 4 - 15 + 6\\ \Leftrightarrow x \le - 5.\end{array}$
Vậy nghiệm của bất phương trình là \(x \le - 5.\)
Bất phương trình $2(x - 1) - x > 3(x - 1) - 2x - 5$ có nghiệm là:
-
A
Vô số nghiệm
-
B
$x < 3,24$
-
C
$x > 2,12$
-
D
Vô nghiệm
Đáp án của giáo viên lời giải hay : A
- Quy tắc chuyển vế.
- Tìm $x.$
Ta có:
$\begin{array}{l}\;\;\;\;\;2(x - 1) - x > 3(x - 1) - 2x - 5\\ \Leftrightarrow 2x - 2 - x > 3x - 3 - 2x - 5\\ \Leftrightarrow x - 2 > x - 8\\ \Leftrightarrow - 2 > - 8\end{array}$
Luôn đúng
Vậy bất phương trình trên có vô số nghiệm.
Tập nghiệm của bất phương trình \(\dfrac{{x - 3}}{{x + 4}} < 0\) là
-
A
$x > 4$
-
B
\( - 4 < x < 3.\)
-
C
\(x < 3\)
-
D
\(x \ne - 4\).
Đáp án của giáo viên lời giải hay : B
Giải bất phương trình dạng \(\dfrac{{A\left( x \right)}}{{B\left( x \right)}} > 0\)
TH1: \(\left\{ \begin{array}{l}A\left( x \right) > 0\\B\left( x \right) > 0\end{array} \right.\)
TH2: \(\left\{ \begin{array}{l}A\left( x \right) < 0\\B\left( x \right) < 0\end{array} \right.\)
Xét \(\dfrac{{x - 3}}{{x + 4}} < 0.\)
Trường hợp 1:
\(\left\{ \begin{array}{l}x - 3 < 0\\x + 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 3\\x > - 4\end{array} \right. \Leftrightarrow - 4 < x < 3.\)
Trường hợp 2:
\(\left\{ \begin{array}{l}x - 3 > 0\\x + 4 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 3\\x < - 4\end{array} \right. \Rightarrow \) Bất phương trình vô nghiệm.
Vậy \( - 4 < x < 3.\)
Tìm giá trị của x để biểu thức $A = \dfrac{{5 - 2x}}{{{x^2} + 4}}$ có giá trị dương
-
A
$x < \dfrac{5}{2}$
-
B
$x > \dfrac{5}{2}$
-
C
\(x = \dfrac{5}{2}\)
-
D
\(x > 2\).
Đáp án của giáo viên lời giải hay : A
- Phân thức nếu có giá trị dương thì tử và mẫu phải cùng dấu.
- Đánh giá mẫu thức để suy ra điều kiện của tử thức.
Xét $A = \dfrac{{5 - 2x}}{{{x^2} + 4}}$
A có giá trị dương \( \Leftrightarrow A > 0.\)
Ta có: \({x^2} \ge 0\;\forall x \Rightarrow {x^2} + 4 > 0\;\forall x \Rightarrow A > 0 \Leftrightarrow 5 - 2x > 0 \Leftrightarrow x < \dfrac{5}{2}.\)
Vậy với $x < \dfrac{5}{2}$ thì A có giá trị dương.
Phương trình \(\left| {x - 1} \right| + \left| {x - 3} \right| = 2x - 1\) có số nghiệm là
-
A
$2$
-
B
$1$
-
C
\(3\)
-
D
\(0\).
Đáp án của giáo viên lời giải hay : B
- Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối.
- Căn cứ vào bảng xét từng khoảng giải bài toán (đối chiếu với điều kiện tương ứng).
Đặt \(\left| {x - 1} \right| + \left| {x - 3} \right| = 2x - 1\;\;\;\left( 1 \right)\)
Xét: \(\begin{array}{l} + )\;\;x - 1 = 0 \Leftrightarrow x = 1\\ + )\;\;x - 3 = 0 \Leftrightarrow x = 3.\end{array}\)
Ta có bảng xét dấu đa thức $x - 1$ và $x - 3$ dưới đây
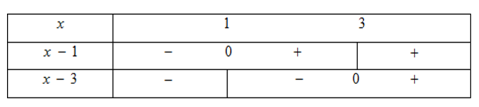
+) Xét khoảng \(x < 1\) ta có:
\((1) \Leftrightarrow (1 - x) + (3 - x) = 2x - 1 \Leftrightarrow - 2x + 4 = 2x - 1 \Leftrightarrow 4x = 5 \Leftrightarrow x = \dfrac{5}{4}\) (Không thuộc khoảng đang xét)
+) Xét khoảng \(1 \le x \le 3\) ta có
\((1) \Leftrightarrow (x - 1) + (3 - x) = 2x - 1 \Leftrightarrow 2 = 2x - 1 \Leftrightarrow x = \dfrac{3}{2}(TM)\)
+) Xét khoảng \(x > 3\) ta có:
\((1) \Leftrightarrow (x - 1) + (x - 3) = 2x - 1 \Leftrightarrow 0.x = - 3\) (phương trình vô nghiệm)
Vậy phương trình có nghiệm \(x = \dfrac{3}{2}\).
Nghiệm của bất phương trình \(\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\) là
-
A
$x < - 1$
-
B
$x < 1$
-
C
\(x > 1\)
-
D
\(x > - 1\).
Đáp án của giáo viên lời giải hay : A
+) Với những bất phương trình chứa ẩn ở mẫu ta đặt điều kiện cho mẫu số khác 0.
+) Quy đồng mẫu thức các phân thức
+) Giải bất phương trình tìm điều kiện của $x$ sau đó đối chiếu với điều kiện để kết luận nghiệm của bất phương trình.
\(\begin{array}{l}\;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\\ \Leftrightarrow \;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\;\;\;\left( * \right)\end{array}\)
Điều kiện \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right..\)
\(\left( * \right) \Leftrightarrow \dfrac{{\left( {x + 4} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \dfrac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < \dfrac{{2{x^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)\( \Leftrightarrow \dfrac{{{x^2} + 3x - 4 + {x^2} + x - 2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\)
\( \Leftrightarrow \dfrac{{4x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\)\( \Leftrightarrow \dfrac{{4\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0 \Leftrightarrow \dfrac{4}{{x + 1}} < 0\) mà \(4 > 0\) nên \(x + 1 < 0 \Leftrightarrow x < - 1.\)
Kết hợp với điều kiện ta có bất phương trình có nghiệm \(x < - 1\).
Tập nghiệm của các bất phương trình ${x^2} + 2(x - 3) - 1 > x(x + 5) + 5$ và $\dfrac{2}{3} - \dfrac{{3x - 6}}{2} > \dfrac{{1 + 3x}}{6}$ lần lượt là
-
A
\({S_1} = \left\{ {x/x > - 4} \right\};\,{S_2} = \left\{ {x/x > \dfrac{7}{4}} \right\}\)
-
B
\({S_1} = \left\{ {x/x > - 4} \right\};\,{S_2} = \left\{ {x/x < \dfrac{7}{4}} \right\}\)
-
C
\({S_1} = \left\{ {x/x < - 4} \right\};\,{S_2} = \left\{ {x/x < \dfrac{7}{4}} \right\}\)
-
D
\({S_1} = \left\{ {x/x < - 4} \right\};\,{S_2} = \left\{ {x/x > \dfrac{7}{4}} \right\}\).
Đáp án của giáo viên lời giải hay : C
+) Qui đồng mẫu số nếu cần
+) Áp dụng quy tắc chuyển vế và liên hệ giữa thứ tự và phép nhân.
+) Khi nhân hay chia cả 2 vế của bất phương trình với một số dương thì bất phương trình không đổi chiều.
+) Khi nhân hay chia cả 2 vế của bất phương trình với một số âm thì bất phương trình đổi chiều.
$\begin{array}{l} + )\;\;{x^2} + 2(x - 3) - 1 > x(x + 5) + 5\\ \Leftrightarrow {x^2} + 2x - 6 - 1 > {x^2} + 5x + 5\\ \Leftrightarrow {x^2} + 2x - {x^2} - 5x > 5 + 6 + 1\\ \Leftrightarrow - 3x > 12\\ \Leftrightarrow x < - 4\end{array}$
Vậy tập nghiệm của bất phương trình trên là: \({S_1} = \left\{ {x/x < - 4} \right\}\)
\(\begin{array}{l} + )\;\;\dfrac{2}{3} - \dfrac{{3x - 6}}{2} > \dfrac{{1 + 3x}}{6}\\ \Leftrightarrow 2.2 - 3(3x - 6) > 1 + 3x\\ \Leftrightarrow 4 - 9x + 18 > 1 + 3x\\ \Leftrightarrow 12x < 21 \Leftrightarrow x < \dfrac{7}{4}\end{array}\)
Vậy tập nghiệm của bất phương trình là \({S_1} = \left\{ {x/x < \dfrac{7}{4}} \right\}\)
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
-
A
\(3\)
-
B
\( - 3\)
-
C
\(1\)
-
D
\( - 1\).
Đáp án của giáo viên lời giải hay : A
Sử dụng: Với $B(x) \ge 0$ thì
\(\left| {A(x)} \right| = B(x) \Rightarrow \left[ \begin{array}{l}A(x) = B(x)\\A(x) = - B(x)\end{array} \right.\)
\(\;\;\left| {{x^2} + 2x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 1 = 2\\{x^2} + 2x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 3 = 0\\{x^2} + 2x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + 3x - x - 3 = 0\\{(x + 1)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x(x + 3) - (x + 3) = 0\\x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}(x + 3)(x - 1) = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 1 = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\\x = - 1\end{array} \right..\)
Vậy nghiệm của phương trình là $x{\rm{ }} = - 3;{\rm{ }}x = \pm 1.$
Tích các nghiệm của phương trình là \(\left( { - 3} \right).1.\left( { - 1} \right) = 3.\)
Chọn câu đúng, biết \(0 < a < b.\)
-
A
\(\dfrac{a}{b} + \dfrac{b}{a} < 2.\)
-
B
\(\dfrac{a}{b} + \dfrac{b}{a} > 2.\)
-
C
\(\dfrac{a}{b} + \dfrac{b}{a} \ge 2.\)
-
D
\(\dfrac{a}{b} + \dfrac{b}{a} = 1.\).
Đáp án của giáo viên lời giải hay : B
Áp dụng thứ tự liên hệ giữa thứ tự và phép cộng, phép nhân.
Biến đổi từ $ (a-b)^2 > 0$ với $0<a<b$ để tìm đáp án đúng.
Với \(0 < a < b\) ta có \({\left( {a - b} \right)^2} > 0\)
\( \Leftrightarrow {a^2} + {b^2} > 2ab \Leftrightarrow \dfrac{{{a^2}}}{{ab}} + \dfrac{{{b^2}}}{{ab}} > 2\,\,\left( {{\rm{do}}\,ab > 0} \right)\)
\( \Leftrightarrow \dfrac{a}{b} + \dfrac{b}{a} > 2.\)
Vậy với mọi \(0 < a < b\) ta luôn có \(\dfrac{a}{b} + \dfrac{b}{a} > 2.\)
Cho số thực \(x\) , chọn câu đúng nhất.
-
A
\({x^4} + 3 \ge 4x\)
-
B
\({x^4} + 5 > {x^2} + 4x\)
-
C
Cả A, B đều sai
-
D
Cả A, B đều đúng.
Đáp án của giáo viên lời giải hay : D
Biến đổi tương đương các bất đẳng thức, sử dụng các hằng đẳng thức để chứng minh.
+) Đáp án A: Bất đẳng thức tương đương với \({x^4} - 4x + 3 \ge 0\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {{x^3} + {x^2} + x - 3} \right) \ge 0 \\\Leftrightarrow \left( {x - 1} \right)\left( {\left( {{x^3} - 1} \right) + \left( {{x^2} + x - 2} \right)} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) + \left( {x - 1} \right)\left( {x + 2} \right)} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 1} \right)\left( {{x^2} + x + 1 + x + 2} \right) \ge 0 \\ \Leftrightarrow {\left( {x - 1} \right)^2}\left( {{x^2} + 2x + 3} \right) \ge 0\\ \Leftrightarrow {\left( {x - 1} \right)^2}\left[ {{{\left( {x + 1} \right)}^2} + 1} \right] \ge 0\end{array}\)
(luôn đúng với mọi số thực $x$)
Đẳng thức xảy ra khi và chỉ khi $x = 1.$
Nên A đúng.
+) Đáp án B: Bất đẳng thức tương đương với \({x^4} - {x^2} - 4x + 5 > 0\)
\( \Leftrightarrow {x^4} - 2{x^2} + 1 + {x^2} - 4x + 4 > 0 \)\( \Leftrightarrow {\left( {{x^2} - 1} \right)^2} + {\left( {x - 2} \right)^2} > 0\)
Ta có: \(\left( {{x^2} - 1} \right) \ge 0,\,\,{\left( {x - 2} \right)^2} \ge 0 \)\( \Leftrightarrow \left( {{x^2} - 1} \right) + {\left( {x - 2} \right)^2} \ge 0\)
Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \pm 1\\x = 2\end{array} \right. \) điều này không xảy ra.
\( \Rightarrow {\left( {{x^2} - 1} \right)^2} + {\left( {x - 2} \right)^2} > 0\) nên B đúng.
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
-
A
\( - 16\)
-
B
\( - 8\)
-
C
\(16\)
-
D
\(8\).
Đáp án của giáo viên lời giải hay : D
Vận dụng tính chất không âm của giá trị tuyệt đối dẫn đến phương pháp bất đẳng thức.
* Nhận xét: Tổng của các số không âm là một số không âm và tổng đó bằng 0 khi và chỉ khi các số hạng của tổng đồng thời bằng 0.
* Cách giải chung: \(\left| A \right| + \left| B \right| = 0\)
Bước1: Đánh giá: \(\left. \begin{array}{l}\left| A \right| \ge 0\\\left| B \right| \ge 0\end{array} \right\} \Rightarrow \left| A \right| + \left| B \right| \ge 0\)
Bước 2: Khẳng định: \(\left| A \right| + \left| B \right| = 0\)\( \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left| {x - 3y} \right| \ge 0\\\left| {y + 4} \right| \ge 0\end{array} \right\} \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} \ge 0\\ \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0 \Leftrightarrow \left\{ \begin{array}{l}x - 3y = 0\\y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3.( - 4) = 0\\y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 12\\y = - 4\end{array} \right.\end{array}\)
Vậy nghiệm của phương trình là $x = - 12$ và $y = - 4.$
Suy ra \(y - x = - 4 - \left( { - 12} \right) = 8.\)
