Trong thí nghiệm Iâng (Y-âng) về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng \(a = 0,5 mm\), khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là \(D = 1,5 m\). Hai khe được chiếu bằng bức xạ có bước sóng \(λ = 0,6 μm\). Trên màn thu được hình ảnh giao thoa. Tại điểm M trên màn cách vân sáng trung tâm (chính giữa) một khoảng \(5,4 mm\) có vân sáng bậc (thứ):
-
A
3
-
B
6
-
C
2
-
D
4
Đáp án của giáo viên lời giải hay : A
Công thức xác định vị trí vân sáng bậc k: xs = ki = kλD/a
Ta có, khoảng vân:
\(i=\dfrac{\lambda D}{a}=\dfrac{0,6.10^{-6}.1,5}{0,5.10^{-3}}=1,8.10^{-3}=1,8mm\)
\({x_M} = 5,4mm = k.1,8 \\\Rightarrow k = \dfrac{{5,4}}{{1,8}} = 3\)
=> Tại M là vân sáng bậc 3
Ánh sáng trên bề mặt rộng 7,2 mm của vùng giao thoa người ta đếm được 9 vân sáng (hai rìa là hai vân sáng). Tại vị trí cách vân trung tâm 14,4 mm ℓà vân:
-
A
Tối thứ 18
-
B
Tối thứ 16
-
C
Sáng thứ 18
-
D
Sáng thứ 16
Đáp án của giáo viên lời giải hay : D
+ Áp dụng biểu thức tính khoảng cách giữa N vân sáng liên tiếp là (N-1)i
+ Áp dụng biểu thức xác định tính chất, vị trí vân sáng - tối
Ta có, trên màn có 9 vân sáng
=> Khoảng cách giữa 9 vân sáng là 8i = 7,2mm => i = 0,9mm
Tại vị trí cách trung tâm 14,4mm = 16i => Vân sáng thứ 16
Một nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng λ = 0,5μm, đến khe Yâng S1, S2 với S1S2 = 0,5mm. Mặt phẳng chứa S1S2 cách màn D = 1m. Tại M trên màn E cách vân trung tâm một khoảng x = 3,5mm ℓà vân sáng hay vân tối, bậc mấy?
-
A
Vân sáng bậc 3
-
B
Vân tối thứ 3
-
C
Vân sáng bậc 4
-
D
Vân tối thứ 4
Đáp án của giáo viên lời giải hay : D
+ Áp dụng biểu thức tính khoảng vân \(i = \frac{{\lambda D}}{a}\)
+ Áp dụng biểu thức xác định tính chất, vị trí vân sáng - tối
Ta có:
+ Khoảng vân \(i = \frac{{\lambda D}}{a} = \frac{{0,{{5.10}^{ - 6}}.1}}{{0,{{5.10}^{ - 3}}}} = {10^{ - 3}}m = 1mm\)
+ Tại M: x = 3,5mm = 3,5i = (3 + 0,5) i
=> Tại M là vân tối bậc 4
Thực hiện thí nghiệm giao thoa khe I-âng với nguồn bức xạ đơn sắc. Điểm M trên màn quan sát có vân sáng bậc 2. Từ vị trí ban đầu của màn, ta dịch chuyển màn ra xa hai khe một đoạn 40 cm thì tại M quan sát thấy vân tối thứ 2. Từ vị trí ban đầu của màn, ta dịch chuyển màn lại gần hai khe một đoạn 40 cm thì tại M quan sát thấy:
-
A
vân sáng bậc 3
-
B
vân sáng bậc 4
-
C
vân tối thứ 4
-
D
vân tối thứ 3
Đáp án của giáo viên lời giải hay : A
Áp dụng lí thuyết về giao thoa sóng ánh sáng, công thức tính khoảng vân i = λD/a
+ Khi chưa dịch màn M: \({x_M} = 2i \Rightarrow i = \frac{{{x_M}}}{2} = \frac{{\lambda D}}{a}\) (1)
+ Khi dịch màn M ra xa một đoạn 40 cm: \({x_M} = 1,5i' \to i' = \frac{{{x_M}}}{{1,5}} = \frac{{\lambda (D + 40)}}{a}\)(2)
Từ (1) và (2) ta có: \(\frac{{D + 40}}{D} = \frac{{i'}}{i} = \frac{{\frac{{{x_M}}}{{1,5}}}}{{\frac{{{x_M}}}{2}}} = \frac{4}{3} \to D = 120(cm)\)
+ Khi dịch màn M lại gần một đoạn 40 cm: \({x_M} = ki'' \Rightarrow i'' = \frac{{{x_M}}}{k} = \frac{{\lambda (D - 40)}}{a}\)(3)
Từ (1) và (3) ta có: \(\frac{{i''}}{i} = \frac{{D - 40}}{D} = \frac{2}{3} = \frac{{\frac{{{x_M}}}{k}}}{{\frac{{{x_M}}}{2}}} = \frac{2}{k} \Rightarrow k = 3\)
Vậy tại M có vân sáng bậc 3
Thực hiện giao thoa ánh sáng với khe Yang, nguồn sáng đơn sắc có bước sóng 400nm, khoảng cách hai khe a = 1mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát D = 3m. Trên màn, xét điểm M cách vân trung tâm một khoảng 10mm. Dịch chuyển màn quan sát từ từ lại gần mặt phẳng chứa hai khe thêm một đoạn 1,2m thì số lần điểm M chuyển thành vân tối là:
-
A
6 lần
-
B
13 lần
-
C
7 lần
-
D
8 lần
Đáp án của giáo viên lời giải hay : A
Sử dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Khoảng vân \(i = \frac{{{{400.10}^{ - 9}}.3}}{{{{10}^{ - 3}}}} = 1,2mm\)
Vị trí điểm M là: x = 8,3.i
Khoảng vân \(i' = \frac{{{{400.10}^{ - 9}}.1,8}}{{{{10}^{ - 3}}}} = 0,72mm\)
Vị trí điểm M là: x = 13,8.i’
Trong quá trình di chuyển, M chuyển thành vân tối ứng với các giá trị: 8,5i; 9,5i; …;13,5i = 6 lần
Một nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng λ= 0,5 μm, đến khe Yâng S1, S2 với S1S2 = 0,5mm. Mặt phẳng chứa S1S2 cách màn D = 1m. Chiều rộng vùng giao thoa quan sát được L = 13mm. Tìm số vân sáng và vân tối quan sát được?
-
A
13 sáng, 14 tối
-
B
11 sáng, 12 tối
-
C
12 sáng, 13 tối
-
D
10 sáng, 11 tối
Đáp án của giáo viên lời giải hay : A
+ Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
+ Áp dụng công thức tính số vân sáng trên màn: \({N_S} = 2\left[ {\frac{L}{{2i}}} \right] + 1 = 13\)
+ Áp dụng biểu thức tính số vân tối trên màn
Ta có:
+ Khoảng vân i: \(i = \frac{{\lambda D}}{a} = \frac{{0,{{5.10}^{ - 6}}.1}}{{0,{{5.10}^{ - 3}}}} = {10^{ - 3}}m = 1mm\)
+ Số vân sáng trên màn: \({N_S} = 2\left[ {\frac{L}{{2i}}} \right] + 1 = 13\)
Ta có: phần thập phân của \(\frac{L}{{2i}} = 0,5\)=> Số vân tối trên màn: Nt = NS + 1 = 14
Trong thì nghiệm Y-âng về giao thoa ánh sáng, nếu ta dùng ánh sáng đơn sắc màu vàng bước sóng 600nm thì đoạn MN (đối xứng hai bên vân sáng trung tâm) ta quan sát được 13 vân sáng. Trong đó tại M và N là các vân sáng. Nếu ta dùng ánh sáng đơn sắc màu xanh có bước sóng 500nm thì trên MN ta quan sát được bao nhiêu vân sáng
-
A
13
-
B
11
-
C
15
-
D
17
Đáp án của giáo viên lời giải hay : C
+ Sử dụng công thức xác định vị trí vân sáng: xS = ki
+ Khoảng cách giữa hai vân sáng liên tiếp là i.
Khi sử dụng bức xạ màu vàng: \(MN = 12{i_1} = 12\frac{{{\lambda _1}D}}{a} \Rightarrow {x_M} = - {x_N} = 6\frac{{{\lambda _1}D}}{a}\).
Khi sử dụng bức xạ màu xanh: \({x_N} = - {x_M} \le n{i_2} \le {x_M} \Leftrightarrow - 6{\lambda _1} \le n{\lambda _2} \le 6{\lambda _1} \Leftrightarrow - 7,2 \le n \le 7,2\)
Có 15 giá trị của n nguyên Có 15 vân sáng
Trong thí nghiệm giao thoa sóng ánh sáng với khoảng cách giữa hai khe ℓà a = 1,5mm. Khoảng cách từ mặt phẳng chứa hai khe tới màn là D = 2m. Hai khe được chiếu sáng bởi ánh sáng đơn sắc có bước sóng λ= 0,48 μm. Vị trí vân sáng bậc hai trên màn ℓà:
-
A
± 2,56 mm
-
B
± 1,32 mm.
-
C
± 1,28 mm.
-
D
± 0,63 mm.
Đáp án của giáo viên lời giải hay : C
+ Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
+ Sử dụng công thức xác định vị trí vân sáng: xS = ki
Ta có:
+ Khoảng vân i: \(i = \frac{{\lambda D}}{a} = \frac{{0,{{48.10}^{ - 6}}.2}}{{1,{{5.10}^{ - 3}}}} = 0,{64.10^{ - 3}}m = 0,64mm\)
+ Vị trí vân sáng bậc 2 trên màn ứng với k = ±2 là: xs2 = ±2i = ±2.0,64 = ±1,28mm
Trong thí nghiệm giao thoa sóng ánh sáng với hai khe Y-âng, ta có a = 0,5mm, D = 2,5m; λ = 0,64 μm. Vị trí vân tối thứ ba kể từ vân sáng trung tâm là:
-
A
±11,2mm
-
B
±6,4mm
-
C
±4,8mm
-
D
±8mm
Đáp án của giáo viên lời giải hay : D
+ Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
+ Sử dụng công thức xác định vị trí vân tối: xt = (k + 0,5)i
Ta có:
+ Khoảng vân \(i = \frac{{\lambda D}}{a} = \frac{{0,{{64.10}^{ - 6}}.2,5}}{{0,{{5.10}^{ - 3}}}} = 3,{2.10^{ - 3}}m = 3,2mm\)
+ Vân tối thứ 3 kể từ vân sáng trung tâm ứng với k = 2 hoặc k = -3\( \to \left[ \begin{array}{l}{x_{t{\rm{ }}(3)}} = \left( {2 + 0,5} \right)i = 8mm\\{x_{t{\rm{ }}(3)}} = \left( { - 3 + 0,5} \right)i = - 8mm\end{array} \right.\)
Thí nghiệm giao thoa sóng ánh sáng với hai khe Yâng trong đó a = 0,3 mm, D = 1m, λ = 600nm. Khoảng cách giữa hai vân sáng bậc 2 và bậc 5 nằm cùng bên vân sáng trung tâm là
-
A
6mm
-
B
3mm
-
C
8mm
-
D
5mm
Đáp án của giáo viên lời giải hay : A
+ Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
+ Áp dụng công thức xác định vị trí vân sáng xs = ki
Ta có:
+ Khoảng vân: \(i = \frac{{\lambda D}}{a} = \frac{{{{600.10}^{ - 9}}.1}}{{0,{{3.10}^{ - 3}}}} = {2.10^{ - 3}}m = 2mm\)
+ Khoảng cách giữa vân sáng bậc 2 và bậc 5 là: 5i - 2i = 3i = 3.2 = 6mm
Thí nghiệm giao thoa ánh sáng với a = 3mm; D = 2,5m, λ= 0,5μm. M, N ℓà hai điểm trên màn nằm hai bên của vân sáng trung tâm và cách vân sáng trung tâm ℓần ℓượt ℓà 2,1mm và 5,9mm. Số vân sáng quan sát được từ M đến N là
-
A
19
-
B
18
-
C
17
-
D
20
Đáp án của giáo viên lời giải hay : D
+ Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
+ Áp dụng công thức tính số vân sáng quan sát được trên màn khi M, N khác phía so với vân trung tâm:
\({N_S} = \left[ {\frac{{ON}}{i}} \right] + \left[ {\frac{{OM}}{i}} \right] + 1\)
Ta có:
+ Khoảng vân: \(i = \frac{{\lambda D}}{a} = \frac{{0,{{5.10}^{ - 6}}.2,5}}{{{{3.10}^{ - 3}}}} = 0,{417.10^{ - 3}}m = 0,417mm\)
+ Số vân sáng quan sát được trên đoạn M,N là:
\({N_S} = \left[ {\frac{{ON}}{i}} \right] + \left[ {\frac{{OM}}{i}} \right] + 1 = \left[ {\frac{{2,1}}{{0,417}}} \right] + \left[ {\frac{{5,9}}{{0,417}}} \right] + 1 = 5 + 14 + 1 = 20\)
Nguồn S phát ánh sáng đơn sắc chiếu sáng hai khe Y-âng cách nhau 0,8mm. Khoảng cách từ mặt phẳng chứa hai khe tới màn ℓà 2,5m. Giữa hai vân sáng ở M và N trên màn cách nhau 22,5mm có 15 vân tối. với tốc độ ánh sáng ℓà c = 3.108 m/s thì tần số của ánh sáng do nguồn S phát ra ℓà
-
A
f = 5,12.1015
-
B
f = 6,25.1014
-
C
f = 8,5.1016Hz
-
D
f = 2,68.1013 Hz.
Đáp án của giáo viên lời giải hay : B
+ Khoảng cách giữa N vân sáng liên tiếp là (N-1)i
+ Áp dụng công thức tính khoảng vân i: \(i = \dfrac{{\lambda D}}{a}\)
+ Áp dụng công thức tính tần số ánh sáng: \(f = \dfrac{c}{\lambda }\)
Ta có:
+ Giữa hai vân sáng ở M và N trên màn cách nhau 22,5mm có 15 vân tối => đoạn MN có 16 vân sáng (kể cả M và N)
=> MN = 22,5mm = 15i => i =1,5mm
+ Khoảng vân i: \(i = \dfrac{{\lambda D}}{a} \to \lambda = \dfrac{{ai}}{D} = \dfrac{{0,{{8.10}^{ - 3}}.1,{{5.10}^{ - 3}}}}{{2,5}} = 0,{48.10^{ - 6}}m\)
+ Tần số của ánh sáng: \(f = \dfrac{c}{\lambda } = \dfrac{{{{3.10}^8}}}{{0,{{48.10}^{ - 6}}}} = 6,{25.10^{14}}H{\rm{z}}\)
Trong thí nghiệm Y-âng, người ta dùng ánh sáng đơn sắc có bước sóng 0,45μm, khoảng cách giữa hai khe là a = 0,45mm. Để trên màn tại vị trí cách vân trung tâm 2,5mm ta có vân sáng bậc 5 thì khoảng cách từ hai khe đến màn là
-
A
1m
-
B
1,5m
-
C
0,5m
-
D
2m
Đáp án của giáo viên lời giải hay : C
+ Áp dụng biểu thức xác định vị trí vân sáng : xs = ki
+Áp dụng công thức tính khoảng vân i: \(i = \frac{{\lambda D}}{a}\)
Để trên màn tại vị trí cách vân trung tâm 2,5mm ta có vân sáng bậc 5 tương đương với 2,5mm = 5i
=> i = 0,5mm
Ta có: Khoảng vân \(i = \frac{{\lambda D}}{a} \to D = \frac{{ai}}{\lambda } = \frac{{{{0,45.10}^{ - 3}}{{.0,5.10}^{ - 3}}}}{{{{0,45.10}^{ - 6}}}} = 0,5m\)
Trong thí nghiệm giao thoa ánh sáng bằng hai khe Y-âng trong không khí người ta thấy tại M trên màn có vân sáng bậc 3. Nếu nhúng toàn bộ hệ thống vào trong nước có chiết suất n = 4/3 thì tại M ta thu được vân gì?
-
A
Vân tối thứ 4
-
B
Vân sáng bậc 4
-
C
Vân tối thứ 6
-
D
Vân sáng bậc 6
Đáp án của giáo viên lời giải hay : B
+ Áp dụng công thức khoảng vân trong môi trường có chiết suất n: \(i' = \frac{{{i_{kk}}}}{n}\)
+ Áp dụng biểu thức xác định vị trí vân sáng - tối trên màn
Gọi : i, i’ lần lượt là khoảng vân của ánh sáng trong không khí và trong nước
Ta có:
+ \(i' = \frac{i}{n}\)
+ Khi đặt hệ trong không khí: xM = 3i
+ Khi đặt hệ trong môi trường nước: \({x_M} = 3i = 3i'.n = 3.\frac{4}{3}i' = 4i'\)
=> Khi nhúng toàn bộ hệ thống vào trong nước thì tại M là vân sáng bậc 4
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát ra ánh sáng đơn sắc có bước sóng \(\lambda_1\). Trên màn quan sát, trên đoạn thẳng MN dài \(20 mm\) (MN vuông góc với hệ vân giao thoa) có \(10\) vân tối, M và N là vị trí của hai vân sáng. Thay ánh sáng trên bằng ánh sáng đơn sắc có bước sóng \(\lambda_2=\dfrac{5\lambda_1}{3}\) thì tại M là vị trí của một vân giao thoa, số vân sáng trên đoạn MN lúc này là:
-
A
7
-
B
5
-
C
8
-
D
6
Đáp án của giáo viên lời giải hay : A
+ Khoảng cách giữa N vân sáng liên tiếp là (N-1)i
+ Áp dụng công thức tính khoảng vân: \(i = \dfrac{{\lambda D}}{a}\)
+ Áp dụng công thức tính số vân sáng trên màn: \({N_S} = 2\left[ {\dfrac{L}{{2i}}} \right] + 1\)
Ta có:
+ Khi dùng ánh sáng có bước sóng λ1 thì trên MN có 10 vân tối => có 11 vân sáng
=> Đoạn \(MN = 20mm = 10i => i = 2mm\)
+ Khi thay λ1 bằng bước sóng λ2 thì có khoảng vân i’
Ta có: \(\dfrac{{i'}}{i} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}} = \dfrac{5}{3} \to i' = \dfrac{5}{3}i = \dfrac{5}{3}.2 = \dfrac{{10}}{3}mm\)
=> Số vân sáng trên đoạn MN: \({N_S} = 2\left[ {\dfrac{L}{{2i'}}} \right] + 1 = 2.3 + 1 = 7\)
Trong thí nghiệm Y-âng về giao thoa ánh sáng, các khe hẹp được chiếu sáng bởi ánh sáng đơn sắc. Khoảng vân trên màn là 1,2mm. Trong khoảng giữa hai điểm N và M trên màn ở cùng một phía so với vân sáng trung tâm, cách vân trung tâm lần lượt 2 mm và 4,5 mm, quan sát được:
-
A
2 vân sáng và 2 vân tối
-
B
3 vân sáng và 2 vân tối
-
C
2 vân sáng và 3 vân tối
-
D
2 vân sáng và 1 vân tối
Đáp án của giáo viên lời giải hay : A
Áp dụng công thức tính số vân sáng - tối trên đoạn MN với M, N cùng phía so với vân sáng trung tâm
+ Số vân sáng: \({N_S} = \left[ {\frac{{OM}}{i}} \right] - \left[ {\frac{{ON}}{i}} \right]\)
+ Số vân tối: \({N_t} = \left[ {\frac{{OM}}{i} + 0,5} \right] - \left[ {\frac{{ON}}{i} + 0,5} \right]\)
Ta có:
+ Số vân sáng trên đoạn MN là: \({N_S} = \left[ {\frac{{OM}}{i}} \right] - \left[ {\frac{{ON}}{i}} \right] = \left[ {\frac{{4,5}}{{1,2}}} \right] - \left[ {\frac{2}{{1,2}}} \right] = 3 - 1 = 2\)
+ Số vân tối trên đoạn MN là: \({N_t} = \left[ {\frac{{OM}}{i} + 0,5} \right] - \left[ {\frac{{ON}}{i} + 0,5} \right] = \left[ {\frac{{4,5}}{{1,2}} + 0,5} \right] - \left[ {\frac{2}{{1,2}} + 0,5} \right] = 4 - 2 = 2\)
Trong thí nghiệm Y-âng về giao thoa ánh sáng với ánh sáng đơn sắc có bước sóng 600(nm), khoảng vân đo được trên màn là 1(mm). Nếu dịch chuyển màn chứa hai khe theo phương vuông góc với màn một đoạn 20(cm) thì khoảng vân đo được là 1,2(mm). Khoảng cách giữa hai khe trong thí nghiệm này là
-
A
1,0 (mm)
-
B
1,2 (mm)
-
C
0,5 (mm)
-
D
0,6 (mm)
Đáp án của giáo viên lời giải hay : D
Sử dụng công thức tính khoảng vân
Ta có: \(\left\{ \begin{array}{l}{i_1} = \frac{{\lambda {D_1}}}{a};{i_2} = \frac{{\lambda {D_2}}}{a}\\{i_2} > {i_1} \Rightarrow {D_2} > {D_1} \Rightarrow {D_2} = {D_1} + 20\end{array} \right. \Rightarrow \frac{{{i_1}}}{{{D_1}}} = \frac{{{i_2}}}{{{D_2}}} \Rightarrow \frac{{{i_1}}}{{{D_1}}} = \frac{{{i_2}}}{{{D_1} + 20}} \Rightarrow {D_1} = 100cm\)
Khoảng cách giữa hai khe: \(a = \frac{{\lambda {D_1}}}{{{i_1}}} = 0,6mm\)
Trong thí nghiệm giao thoa Y-âng, khoảng cách hai khe là 0,5mm. Giao thoa thực hiện với ánh sáng đơn sắc có bước sóng λ thì tại điểm M cách vân sáng trung tâm 1 mm là vị trí vân sáng bậc 2. Nếu dịch màn xa thêm một đoạn 50/3 cm theo phương vuông góc với mặt phẳng hai khe thì tại M là vị trí vân tối thứ 2. Bước sóng ánh sáng dùng trong thí nghiệm bằng
-
A
0,4 µm
-
B
0,5 µm
-
C
0,6 µm
-
D
0,64 µm
Đáp án của giáo viên lời giải hay : B
Sử dụng công thức xác định vị trí vân sáng, vân tối
\(\left\{ \begin{array}{l}{x_M} = 2\frac{{\lambda D}}{a} = 1mm\\{x_M} = 1,5\frac{{\lambda \left( {D + 0,5/3} \right)}}{a} = 1mm\end{array} \right. \Rightarrow \lambda = 0,{5.10^{ - 6}}\left( m \right) = 0,5\mu m\)
Thí nghiệm Y - âng về giao thoa ánh sáng với ánh sáng đơn sắc có bước sóng λ, khoảng cách hai khe a = 0,8mm. Ban đầu, tại M cách vân trung tâm 5,25mm người ta quan sát được vân sáng bậc 5. Giữ cố định các điều kiện khác, di chuyển từ từ màn quan sát ra xa dọc theo đường thẳng vuông góc với màn chứa hai khe một đoạn 0,75m thì thấy tại M chuyển thành vân tối lần thứ hai. Bước sóng λ có giá trị là
-
A
0,50μm
-
B
0,70μm
-
C
0,48μm
-
D
0,64μm
Đáp án của giáo viên lời giải hay : C
Sử dụng công thức xác định vị trí vân sáng, vân tối
Ban đầu tại M quan sát được vân sáng bậc 5 \( \Rightarrow 5,{25.10^{ - 3}} = \frac{{5\lambda D}}{{0,{{8.10}^{ - 3}}}} \Rightarrow \lambda D = 0,84\mu m\)
Di chuyển màn quan sát đến khi ở M là vân tối lần thứ 2 vân sáng ở M sẽ chuyển thành vân tối thứ 5, rồi vân tối thứ 4 khi di chuyển dần màn quan sát ra xa.
\(5,{25.10^{ - 3}} = \frac{{3,5\lambda (D + 0,75)}}{{0,{{8.10}^{ - 3}}}} \Rightarrow \lambda = 0,48\mu m\)
Thí nghiệm giao thoa Y-âng với ánh sáng đơn sắc có bước sóng λ, khoảng cách giữa hai khe a = 1 mm. Ban đầu, tại M cách vân trung tâm 5,25 mm người ta quan sát được vân sáng bậc 5. Giữ cố định màn chứa hai khe, di chuyển từ từ màn quan sát ra xa và dọc theo đường thẳng vuông góc với mặt phẳng chứa hai khe một đoạn 0,75 m thì thấy tại M chuyển thành vân tối lần thứ hai. Bước sóng λ có giá trị là
-
A
0,64 µm
-
B
0,7 µm
-
C
0,6 µm
-
D
0,5 µm
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về giao thoa ánh sáng
+ Ban đầu khi chưa di chuyển màn, khoảng cách giữa hai khe đến màn là D
Khi đó xM = 5,25mm = 5i
+ Sau khi di chuyển màn ra xa 0,75m khoảng cách giữa hai khe đến màn là D + 0,75 (m)
Khi đó M chuyển thành vân tối lần thứ 2 xM = 3,5i’
\( \Rightarrow \frac{{i'}}{i} = \frac{{10}}{7} = \frac{{D'}}{D} = \frac{{D + 0,75}}{D} \Rightarrow D = 1,75(m)\)
=> Bước sóng: \(\lambda = \frac{{ia}}{D} = \frac{{1,05.1}}{{1,75}} = 0,6(\mu m)\)
Cho thí nghiệm Y-âng, ánh sáng có bước sóng 500 nm. M là chân đường cao hạ vuông góc từ S1 tới màn E. Lúc đầu người ta thấy M là một cực đại giao thoa. Dịch màn E ra xa hai khe S1,S2 đến khi tại M bị triệt tiêu năng lượng sáng lần thứ nhất thì độ dịch là 1/7 m. Để năng lượng tại M lại bị triệt tiêu thì phải dịch màn xa thêm ít nhất là 16/35 m. Khoảng cách từ hai khe S1, S2 đến màn ảnh M lúc đầu là
-
A
2m
-
B
1,8m
-
C
1m
-
D
0,5m
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về giao thoa sóng ánh sáng
Công thức xác định vị trí vân sáng, vân tối: xs = kλD/a; xt = (k + ½)λD/a
- Ban đầu M là một cực đại giao thoa bậc k nên :
\({x_M} = \frac{a}{2} = \frac{{k\lambda D}}{a} \to {a^2} = 2k\lambda D\left( 1 \right)\)
- Dịch màn ra xa hai khe thêm 1/7 m đến khi tại M là vân tối lần thứ nhất => vân tối tại M ứng với (k - 1) (vì khi D tăng thì i tăng)
\( \Rightarrow {x_M} = \frac{a}{2} = \left( {k - 1 + \frac{1}{2}} \right)\frac{\lambda }{a}\left( {D + \frac{1}{7}} \right) \Rightarrow {a^2} = 2\left( {k - \frac{1}{2}} \right)\lambda \left( {D + \frac{1}{7}} \right)\left( 2 \right)\)
- Dịch màn ra xa hai khe thêm 16/35 m đến khi tại M là vân tối lần thứ 2 => vân tối tại M ứng với (k - 2) \( \Rightarrow {x_M} = \frac{a}{2} = (k - 2 + \frac{1}{2}{\rm{)}}\frac{{\lambda \left( {D + \frac{1}{7} + \frac{{16}}{{35}}} \right)}}{a} \Rightarrow {a^2} = 2\left( {k-1,5} \right)\lambda \left( {D{\rm{ }} + {\rm{ }}0,6} \right){\rm{ }}\left( 3 \right)\)
- Từ (1) và (2) suy ra : \(2k\lambda D = 2\left( {k - 0,5} \right)\lambda \left( {D + \frac{1}{7}} \right) \Rightarrow 7D = 2k + 1\) (4)
- Từ (1) và (3) suy ra : \(2k\lambda D = 2\left( {k - 1,5} \right)\lambda \left( {D + 0,6} \right) \Rightarrow 1,5D = 0,6k + 0,9\) (5)
- Lập tỉ số (4) : (5) => k = 4 => D = 1m
Trong một thí nghiệm Yâng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,5 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2 m. Nguồn sáng phát ra ánh sáng trắng có bước sóng trong khoảng từ 380 nm đến 760 nm. M là một điểm trên màn, cách vân trung tâm 2 cm. Trong các bức xạ cho vân sáng tại M, tổng giữa bức xạ có bước sóng dài nhất và bức xạ có bước sóng ngắn nhất là
-
A
570 nm
-
B
760 nm
-
C
417 nm
-
D
1099 nm
Đáp án của giáo viên lời giải hay : D
Khoảng vân: \(i = \dfrac{{\lambda D}}{a}\)
Vị trí vân sáng: \(x = ki = k\dfrac{{\lambda D}}{a}\)
Tại M cho vân sáng, ta có:
\({x_M} = k\dfrac{{\lambda D}}{a} \Rightarrow 0,02 = k\dfrac{{\lambda .2}}{{0,{{5.10}^{ - 3}}}} \Rightarrow k\lambda = {5.10^{ - 6}}\)
Mà \(380\,\,nm \le \lambda \le 760\,\,nm \Rightarrow 13,15 \ge k \ge 6,58\)
Bước sóng dài nhất tại M tương ứng với: \({k_{\min }} = 7 \Rightarrow {\lambda _{\max }} = 7,{14.10^{ - 7}}\,\,\left( m \right) = 714\,\,\left( {nm} \right)\)
Bước sóng ngắn nhất tại M tương ứng với: \({k_{\max }} = 13 \Rightarrow {\lambda _{\min }} = 3,{85.10^{ - 7}}\,\,\left( m \right) = 385\,\,\left( {nm} \right)\)
Tổng giữa bức xạ có bước sóng dài nhất và bức xạ có bước sóng ngắn nhất là:
\({\lambda _{\max }} + {\lambda _{\min }} = 714 + 385 = 1099\,\,\left( {nm} \right)\)
Khi thực hiện thí nghiệm I – âng về giao thoa ánh sáng với một ánh sáng đơn sắc có bước sóng \(\lambda \), tại điểm M trên màn có vân sáng bậc hai. Khi thay nguồn sáng bằng ánh sáng có bước sóng \(\left( {\lambda -0,2\mu m} \right)\), tại M có vân sáng bậc ba. Bước sóng \(\lambda \) bằng
-
A
\(0,5\mu m\)
-
B
\(0,4\mu m\)
-
C
\(0,7\mu m\)
-
D
\(0,6\mu m\)
Đáp án của giáo viên lời giải hay : D
Vị trí vân sáng bậc k: $x=k\frac{\lambda D}{a}$
Khi giao thoa với ánh sáng có bước sóng \(\lambda \) thì tại M là vân sáng bậc 2 là:
\({{x}_{M}}=k\frac{\lambda D}{a}=2\frac{\lambda D}{a}\,\,\left( 1 \right)\)
Khi giao thoa với ánh sáng có bước sóng \(\left( {\lambda -0,2\mu m} \right)\) thì tại M là vân sáng bậc 3 là:
\({{x}_{M}}=3\frac{\left( \lambda -0,{{2.10}^{-6}} \right)D}{a}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có:
\(\begin{align}& 2\frac{\lambda D}{a}=3\frac{\left( \lambda -0,{{2.10}^{-6}} \right)D}{a} \\& \Rightarrow 2\lambda =3\left( \lambda -0,{{2.10}^{-6}} \right) \\& \Rightarrow \lambda =0,{{6.10}^{-6}}\,\,\left( m \right)=0,6\,\,\left( \mu m \right) \\\end{align}\)
Thực hiện thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng điểm S phát ra ánh sáng đơn sắc có bước sóng 500 nm. Khoảng cách giữa hai khe S1 và S2 là 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2 m. Ban đầu, S đặt tại điểm O nằm trên đường trung trực của S1S2 và cách mặt phẳng chứa hai khe 50 cm. Xét trục Ou song song với màn và vuông góc với mặt phẳng trung trực của hai khe S1S2 như hình vẽ, trong đó 0 là gốc tọa độ. Giữ nguyên các điều kiện khác, cho S dao động điều hòa trên trục Ou với phương trình \(u = \cos \left( {2\pi t + \dfrac{\pi }{2}} \right)\,\,\left( {mm} \right)\), trong đó t tính bằng s. Tính từ thời điểm ban đầu t = 0, thời điểm vị trí chính giữa trên màn quan sát có nháy sáng lần thứ 2021 là
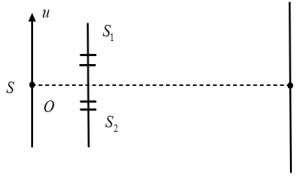
-
A
216,75 s.
-
B
224,75 s.
-
C
126,25 s.
-
D
112,25 s.
Đáp án của giáo viên lời giải hay : C
Điểm chính giữa trên màn có nháy sáng khi tại đó là vân sáng
Khoảng vân: \(i = \dfrac{{\lambda D}}{a}\)
Dịch chuyển màn một đoạn x theo phương thẳng đứng, vân sáng trung tâm dịch chuyển một đoạn: \(\left| y \right| = \dfrac{{Dx}}{d}\)
Chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\)
Khoảng vân giao thoa là:
\(i = \dfrac{{\lambda D}}{a} = \dfrac{{{{500.10}^{ - 9}}.2}}{{{{1.10}^{ - 3}}}} = {1.10^{ - 3}}\,\,\left( m \right) = 1\,\,\left( {mm} \right)\)
Điểm chính giữa trên màn I có nháy sáng khi tại đó có vân sáng
Độ dịch chuyển cực đại của vân trung tâm trên màn là:
\({y_{\max }} = \dfrac{{D.{x_{\max }}}}{d} = \dfrac{{{{2.1.10}^{ - 3}}}}{{0,5}} = {4.10^{ - 3}}\,\,\left( m \right) = 4\,\,\left( {mm} \right) = 4i\)
→ trong \(\dfrac{1}{4}\) chu kì điểm sáng S dịch chuyển từ vị trí cân bằng đến biên, tại điểm I có 4 lần tạo vân sáng
→ trong 1 chu kì, tại điểm I có vân sáng 16 lần
Chu kì dao động của điểm sáng S là:
\(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1\,\,\left( s \right)\)
Thời điểm ban đầu điểm sáng S ở vị trí cân bằng, điểm I có nháy sáng lần đầu tiên
Điểm I có nháy sáng lần thứ 2021 khi điểm sáng S thực hiện số chu kì là:
\(n = \dfrac{{2021 - 1}}{{16}} = 126,25 \Rightarrow t = nT = 126,25\,\,\left( s \right)\)
Thực hiện thí nghiệm Yâng về giao thoa với ánh sáng đơn sắc màu lam ta quan sát được hệ vân giao thoa trên màn. Nếu thay ánh sáng đơn sắc màu lam bằng ánh sáng đơn sắc màu vàng và các điều kiện khác của thí nghiệm được giữ nguyên thì
-
A
Khoảng vân tăng lên.
-
B
Khoảng vân giảm xuống.
-
C
Vị trí vân trung tâm thay đổi.
-
D
Khoảng vân không thay đổi.
Đáp án của giáo viên lời giải hay : A
Khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Khi thay ánh sáng đơn sắc có bước sóng khác, vị trí vân trung tâm không thay đổi
Khoảng vân giao thoa: \(i = \frac{{\lambda D}}{a} \Rightarrow i \sim \lambda \)
Ta có bước sóng: \({\lambda _v} > {\lambda _l} \Rightarrow {i_v} > {i_l}\)
Một học sinh làm thí nghiệm đo bước sóng ánh sáng bằng thí nghiệm khe Y-âng. Trong khi tiến hành, học sinh này đo được khoảng cách hai khe sáng là \(1,00 \pm 0,05\left( {mm} \right)\); khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \(2000 \pm 1,54\left( {mm} \right)\); khoảng cách 10 vân sáng liên tiếp đo được là \(10,80 \pm 0,14\left( {mm} \right)\). Sai số tuyệt đối của quá trình đo bước sóng là
-
A
\( \pm 0,034\mu m\)
-
B
\( \pm 0,039\mu m\)
-
C
\( \pm 0,26\mu m\)
-
D
\( \pm 0,019\mu m\)
Đáp án của giáo viên lời giải hay : B
Khoảng cách của 10 vân sáng liên tiếp: \(l = 9i\)
Bước sóng: \(\lambda = \dfrac{{ai}}{D}\)
Sai số tỉ đối: \(\dfrac{{\Delta \lambda }}{{\overline \lambda }} = \dfrac{{\Delta a}}{{\overline a }} + \dfrac{{\Delta i}}{{\overline i }} + \dfrac{{\Delta D}}{{\overline D }}\)
Sai số tuyệt đối: \(\Delta \lambda = \bar \lambda \left( {\dfrac{{\Delta a}}{{\bar a}} + \dfrac{{\Delta i}}{{\bar i}} + \dfrac{{\Delta D}}{{\bar D}}} \right)\)
Khoảng cách giữa 10 vân sáng liên tiếp là:
\(l = 9i \Rightarrow \left\{ \begin{array}{l}\overline i = \dfrac{{\overline l }}{9} = 1,2\,\,\left( {mm} \right)\\\Delta i = \dfrac{{\Delta l}}{9} = 0,016\,\,\left( {mm} \right)\end{array} \right.\)
Giá trị trung bình của bước sóng là:
\(\overline \lambda = \dfrac{{\overline a .\overline i }}{{\overline D }} = \dfrac{{{{1.10}^{ - 3}}.1,{{2.10}^{ - 3}}}}{2} = 0,{6.10^{ - 6}}\,\,\left( m \right) = 0,6\,\,\left( {\mu m} \right)\)
Sai số tỉ đối của phép đo là:
\(\begin{array}{l}\dfrac{{\Delta \lambda }}{{\overline \lambda }} = \dfrac{{\Delta a}}{{\overline a }} + \dfrac{{\Delta i}}{{\overline i }} + \dfrac{{\Delta D}}{{\overline D }}\\ \Rightarrow \dfrac{{\Delta \lambda }}{{0,6}} = \dfrac{{0,05}}{1} + \dfrac{{0,016}}{{1,2}} + \dfrac{{1,54}}{{2000}}\\ \Rightarrow \Delta \lambda \approx \pm 0,038\,\,\left( {\mu m} \right)\end{array}\)
