Trong một thí nghiệm về giao thoa ánh sáng. Hai khe Y-âng cách nhau 3mm, hình ảnh giao thoa được hứng trên màn cách hai khe 3m. Sử dụng ánh sáng trắng có bước sóng từ 0,38μm đến 0,76μm. Trên màn quan sát thu được các dải quang phổ. Bề rộng của dải quang phổ ngay sát vạch sáng trắng trung tâm là:
-
A
0,38 mm
-
B
0,45 mm
-
C
0,5 mm
-
D
0,55 mm
Đáp án của giáo viên lời giải hay : A
Quang phổ ngay sát vạch sáng trung tâm là quang phổ bậc 1
Công thức tính bề rộng quang phổ bậc n : ∆xn = xđn - xtn
Bề rộng quang phổ bậc 1 là:
\(\Delta {x_1} = {x_{d1}} - {x_{t1}} = \frac{D}{a}\left( {{\lambda _d} - {\lambda _t}} \right) = \frac{3}{3}\left( {0,76 - 0,38} \right) = 0,38\,mm\)
Trong thí nghiệm Iâng khoảng cách giữa hai khe là 2mm, khoảng cách từ hai khe đến màn là 2m. Nguồn S phát ánh sáng trắng có bước sóng từ 0,38μm đến 0,76μm. Vùng phủ nhau giữa quang phổ bậc hai và bậc ba có bề rộng là:
-
A
0,38mm
-
B
1,14 mm
-
C
0,76 mm
-
D
1,52 mm
Đáp án của giáo viên lời giải hay : A
Sử dụng lí thuyết về giao thoa ánh sáng trắng
Bề rộng quang phổ bậc n là : ∆xn = xđn - xtn
Vùng phủ nhau giữa quang phổ bậc hai và bậc ba có bề rộng là: \(\Delta x{\rm{ }} = {x_{d2}}--{x_{t3}} = \left( {2{\lambda _d} - {\rm{ }}3{\lambda _t}} \right)\frac{D}{a} = 0,38{\rm{ }}mm\)
Trong thí nghiệm I âng về giao thoa ánh sáng, khoảng cách giữa hai khe \(a = 2mm\), khoảng cách từ hai khe đến màn ảnh \(D = 2m\). Nguồn S phát ánh sáng trắng có bước sóng từ \(0,38\mu m\) đến \(0,76\mu m\). Vùng phủ nhau giữa quang phổ bậc ba và bậc bốn có bề rộng là
-
A
0,38 mm
-
B
0,76 mm
-
C
1,52 mm
-
D
0
Đáp án của giáo viên lời giải hay : B
Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức xác định vị trí vân sáng
Bề rộng quang phổ bậc n là : ∆xn = xđn - xtn
Ta có vùng phủ nhau giữa quang phổ bậc 3 với quang phổ bậc 4 là khoảng từ xđ3 tới xt4.
\({x_{d3}} = 3\frac{{{\lambda _d}.D}}{a};\,\,{x_{t4}} = 4\frac{{{\lambda _t}.D}}{a}\,\, \Rightarrow \,\,\,\Delta x = {x_{d3}} - {x_{t4}} = \left( {3{\lambda _d} - 4{\lambda _t}} \right).\frac{D}{a} = 0,76\left( {mm} \right)\,\,\,\,\,\,\,\,\,\)
Trong một thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,5 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2 m. Nguồn sáng phát ánh sáng trắng có bước sóng trong khoảng từ 380 nm đến 760 nm. M là một điểm trên màn, cách vân sáng trung tâm 2 cm. Trong các bức xạ cho vân sáng tại M, bức xạ có bước sóng dài nhất là:
-
A
417 nm
-
B
570 nm
-
C
714 nm
-
D
760 nm
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về giao thoa sóng ánh sáng, điều kiện để một điểm là vị trí vân sáng
Vị trí vân sáng: xs = kλD/a
D = 2m, a = 0,5mm = 0,5.10-3m
Tại M cho vân sáng: \({x_M} = 20mm = \frac{{k\lambda D}}{a} \Rightarrow \lambda = \frac{{20.a}}{{kD}} = \frac{5}{k}\mu m\)
Với: \(0,38\mu m \le \lambda \le 0,76\mu m \leftrightarrow 0,38\mu m \le \frac{5}{k} \le 0,76\mu m \leftrightarrow 6,57 \le k \le 13,16\)
Vậy kmin = 7 => λmax = 0,714μm = 714nm
Thực hiện giao thoa với ánh sáng trắng (0,38μm ≤ λ ≤ 0,76µm) bằng hai khe Y – âng cách nhau 0,1 mm. Khoảng cách từ hai khe đến màn là 80 cm. Ánh sáng đơn sắc cho vân sáng tại vị trí cách vân sáng trung tâm 3,2 cm có bước sóng ngắn nhất là
-
A
0,38μm
-
B
0,44μm
-
C
0,4μm
-
D
0,67μm
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức xác định vị trí vân sáng
Vị trí vân sáng: xs = kλD/a
\(x = \frac{{k\lambda D}}{a} = 32mm \Rightarrow \lambda = \frac{4}{k}\mu m\)
Có: \(0,38\mu m \le \lambda \le 0,76\mu m \Leftrightarrow 0,38\mu m \le \frac{4}{k} \le 0,76\mu m \Rightarrow 5,26 \le k \le 10,5 \Rightarrow k = 6;7;8;9;10\)
Bước sóng λ nhỏ nhất nên k phải lớn nhất => kmax = 10 => λ = 0,4µm
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 1mm, khoảng cách từ hai khe đến màn là 1,2m. Nguồn S phát áng sáng trắng có bước sóng từ 0,40μm đến 0,76μm. Tần số lớn nhất của bức xạ đơn sắc cho vân sáng tại điểm M trên màn cách vân trung tâm một đoạn 2,7mm là
-
A
3,94.1014Hz.
-
B
7,5.1014Hz.
-
C
7,8.1014Hz.
-
D
6,67.1014Hz.
Đáp án của giáo viên lời giải hay : D
Sử dụng lí thuyết giao thoa ánh sáng
Vị trí vân sáng: xs = kλD/a
+ M cách vân trung tâm đoạn 2,7 mm cho vân sáng => ${x_M} = k\frac{{\lambda D}}{a} = > \lambda = \frac{{{x_M}a}}{{kD}} = \frac{{2,7.1}}{{1,2k}} = \frac{{2,25}}{k}(k \in Z)$
+ Mà bước sóng nằm trong khoảng từ 0,40 µm đến 0,76 µm
=> \(0,4 \le \frac{{2,25}}{k} \le 0,76 = > 2,96 \le k \le 5,63\) => k: 3,4,5
=> Tần số lớn nhất của bức xạ cho vân sáng tại M, ứng với bước sóng ngắn nhất (k = 5)
=> λmin = 0,45µm là: \(f = \frac{c}{\lambda } = \frac{{{{3.10}^8}}}{{0,{{45.10}^{ - 6}}}} = 6,{67.10^{14}}(Hz)\)
Trong một thí nghiệm Y – âng về giao thoa ánh sáng, nguồn sáng phát ánh sáng trắng có bước sóng trong khoảng 380nm đến 760nm. M là một điểm trên màn, ứng với vị trí vân sáng bậc 5 bước sóng 600nm. Bước sóng ngắn nhất cho vân tối tại M là:
-
A
387nm
-
B
414nm
-
C
400nm
-
D
428nm
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức xác định vị trí vân sáng, vân tối
Vị trí vân sáng và vân tối: \({x_s} = \frac{{k\lambda D}}{a};{x_t} = \left( {k + \frac{1}{2}} \right)\frac{{\lambda D}}{a}\)
Hai bức xạ trùng nhau: x1 = x2
\({x_M} = 5\frac{{0,6D}}{a} = \left( {k + \frac{1}{2}} \right)\frac{{\lambda D}}{a} \to \lambda = \frac{6}{{2k + 1}}\mu m\)
\(0,38\mu m \le \lambda \le 0,76\mu m \Leftrightarrow 0,38 \le \frac{6}{{2k + 1}} \le 0,76 \to k = 7,6,5,4\)
Bước sóng ngắn nhất ứng với k lớn nhất k = 7 =>\(\lambda = 0,4\mu m = 400nm\)
Thực hiện thí nghiệm I - âng về giao thoa ánh sáng . Khoảng cách giữa hai khe là \(1mm\), khoảng cách từ màn quang sát tới 2 khe là \(2m\). Chiếu sáng hai khe bằng ánh sáng trắng có bước sóng \(400nm ≤ λ ≤ 750 µm\). Bước sóng lớn nhất của các bức xạ cho vân tối tại điểm N trên màn, cách vân trung tâm \(12mm\) là
-
A
735 nm
-
B
685 nm
-
C
635 nm
-
D
705 nm
Đáp án của giáo viên lời giải hay : D
Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức xác định vị trí vân tối
Vị trí vân tối: \({x_t} = \left( {k + \dfrac{1}{2}} \right)\frac{{\lambda D}}{a}\)
\({x_N} = \left( {k + \dfrac{1}{2}} \right)\dfrac{{\lambda D}}{a} = 12mm \\\Rightarrow \lambda = \dfrac{{12a}}{{\left( {k + 0,5} \right)D}} = \dfrac{6}{{\left( {k + 0,5} \right)}} (\mu m)\)
\(400 nm \le \lambda \le 750nm\\\Leftrightarrow 0,4\mu m \le \lambda \le 0,75 \mu m\)
\(\Leftrightarrow 0,4\mu m \le \dfrac{6}{{k + 0,5}} (\mu m) \le 0,75 \mu m \)
\(\Leftrightarrow 7,5 \le k \le 14,5\)
Để \(\lambda_{max}\) thì \(k_{min}=8 \to \lambda = 0,705 \mu m = 705nm\)
Trong thí nghiệm Young về giao thoa ánh sáng, nếu sử dụng ánh sáng trắng có bước sóng 400nm đến 750nm. Tại vị trí của vân sáng bậc 3 của ánh sáng tím bước sóng 400nm còn có vân sáng của ánh sáng đơn sắc có bước sóng
-
A
700nm
-
B
650nm
-
C
500nm
-
D
600nm
Đáp án của giáo viên lời giải hay : D
Sử dụng lí thuyết về giao thoa với ánh sáng trắng
Hai vân sáng trùng nhau: x1 = x2 <=> k1λ1 = k2λ2
Vị trí của vân sáng bậc 3 của sáng tím trùng với vân sáng của ánh sáng đơn sắc khác
Sử dụng điều kiện của 2 vân sáng trùng nhau ta có:
\(\frac{{{k_1}{\lambda _1}D}}{a} = \frac{{{k_2}.{\lambda _2}D}}{a} \Leftrightarrow {k_1}{\lambda _1} = {k_2}.{\lambda _2} \Leftrightarrow 3.400 = {k_2}.{\lambda _2} \Leftrightarrow {\lambda _2} = \frac{{1200}}{{{k_2}}}\) trong đó \({k_1},{k_2}\) là số nguyên
Mà: \(400 \le {\lambda _2} \le 750 \Leftrightarrow 400 < \frac{{1200}}{{{k_2}}} \le 750 \Rightarrow {k_2} = 2 \Rightarrow {\lambda _2} = 600nm\)
Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng từ 0,38 µm đến 0,76 µm. Tại vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng 0,76 µm còn có bao nhiêu vân sáng nữa của các ánh sáng đơn sắc khác?
-
A
3
-
B
8
-
C
7
-
D
4
Đáp án của giáo viên lời giải hay : D
Sử dụng lí thuyết về giao thoa ánh sáng trắng
Vị trí vân sáng: xs = kλD/a
+ Gọi M là vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng 0,76 µm ta có: \({x_M} = 4{i_1} = \frac{{4{\lambda _1}D}}{a}\)
+ M còn là vị trí vân sáng của các ánh sáng có bước sóng khác, do đó ta có:
\({x_M} = ki = \frac{{k\lambda D}}{a} = \frac{{4{\lambda _1}D}}{a} = > \lambda = \frac{{4{\lambda _1}}}{k}\)
Mà \(0,38 \le \lambda \le 0,76 = > 0,38 \le \frac{{4{\lambda _1}}}{k} \le 0,76 = > 4 \le k \le 8\)
Do đó k: 4,5,6,7,8 với k = 4 chính là ánh sáng có bước sóng 0,76 µm
=> Tại M còn 4 vân sáng nữa của các ánh sáng đơn sắc khác
Trong thì nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 2 mm, khoảng cách từ mặt phẳng chứa 2 khe đến màn quan sát là 2 m. Nguồn phát ánh sáng gồm các bức xạ đơn sắc có bước sóng trong khoảng 0,40 µm đến 0,76 µm. Trên màn, tại điểm cách vân trung tâm 3,3 mm có bao nhiêu bức xạ cho vân sáng?
-
A
3
-
B
4
-
C
5
-
D
6
Đáp án của giáo viên lời giải hay : B
Sử dụng điều kiện để một điểm là vân sáng trong giao thoa sóng ánh sáng
Vị trí vân sáng: xs = kλD/a
Để M là vân sáng thì \({x_M} = ki = \frac{{k\lambda D}}{a} = > \lambda = \frac{{{x_M}a}}{{kD}} = \frac{{3,3}}{k}\)
Bước sóng nằm trong khoảng 0,40 µm đến 0,76 µm =>\(0,4 \le \frac{{3,3}}{k} \le 0,76 = > 4,34 \le k \le 8,25 = > k=5,6,7,8\)
=> có $4$ bức xạ
Trong thí nghiệm Iâng, hai khe được chiếu sáng bằng ánh sáng trắng (có bước sóng từ 0,38µm đến 0,76µm). Khi đó taị vị trí vân sáng bậc 3 của ánh sáng đỏ (λđỏ = 0,75µm), còn có thêm bao nhiêu bức xạ đơn sắc cho vân sáng tại đó?
-
A
2
-
B
3
-
C
4
-
D
5
Đáp án của giáo viên lời giải hay : A
Sử dụng lí thuyết về giao thoa ánh sáng trắng
Hai vân sáng trùng nhau : x1 = x2 <=> k1λ1 = k2λ2
Gọi \(\lambda \) là bước sóng cho vân sáng tại vị trí vân sáng bậc 3 của ánh sáng đỏ:
\(k\lambda = 3{\lambda _d} \to \lambda = \dfrac{{3{\lambda _d}}}{k} = \dfrac{{3.0,75}}{k} = \dfrac{{2,25}}{k}\mu m\)
Mà:
\(\begin{array}{l}0,38\mu m \le \lambda \le 0,76\mu m\\ \Leftrightarrow 0,38 \le \frac{{2,25}}{k} \le 0,76\\ \Leftrightarrow 2,96 \le k \le 5,92\\ \Rightarrow k = 3;4;5\end{array}\)
Ta có \(k = 3\) ứng với vân sáng bậc 3 của ánh sáng đỏ tại vị trí đó
=> Trừ ánh sáng đỏ đi qua thì còn 2 bức xạ khác
Trong thí nghiệm Y-âng về giao thoa ánh sáng với nguồn ánh sáng trắng có bước sóng trong khoảng (0,38μm ≤ λ ≤ 0,76µm), hai khe hẹp cách nhau 1mm. Bề rộng quang phổ bậc 1 lúc đầu đo được là 0,38mm. Khi dịch chuyển màn ra xa hai khe thêm một đoạn thì bề rộng quang phổ bậc 1 trên màn lúc này đo được là 0,57mm. Màn đã dịch chuyển một đoạn là
-
A
50 cm
-
B
40 cm
-
C
45 cm
-
D
55 cm
Đáp án của giáo viên lời giải hay : A
Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức tính bề rộng quang phổ
Bề rộng quang phổ bậc n: ∆xn = xđn - xtn
\(\Delta x = \frac{{D({\lambda _d} - {\lambda _t})}}{a} = 0,38mm\)
Thay dữ liệu vào công thức trên suy ra D = 1m
\(\Delta x' = \frac{{(D + x)({\lambda _d} - {\lambda _t})}}{a} = 0,57mm \Rightarrow x = 0,5m = 50cm\)
Trong thí nghiệm Iâng (Young) về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng từ 0,38 mm đến 0,76mm. Tại vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng 0,76 mm , người ta đặt khe hẹp F của ống chuẩn trực máy quang phổ lăng kính thì trên kính ảnh của buồng tối máy quang phổ này quan sát được:
-
A
ba vạch sáng riêng lẻ .
-
B
bốn vạch sáng riêng lẻ .
-
C
năm vạch sáng riêng lẻ.
-
D
một dải màu liên tục
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức xác định vị trí vân sáng
Vị trí vân sáng: \({x_s} = \dfrac{{\lambda D}}{a}\)
Theo bài ra ta có, vị trí vân sáng bậc 4 của ánh sáng có bước sóng \({\lambda _1} = 0,76\mu m\)
\({x_1} = {k_1}{i_1} = {k_1}\dfrac{{{\lambda _1}D}}{a}\)
Cũng tại vị trí này, để tại đó là vân sáng của bức xạ \(\lambda \) khác thì: \({x_2} = ki = k\dfrac{{\lambda D}}{a}\)
Ta có:
\(\begin{array}{l}{x_1} = {x_2} \Leftrightarrow {k_1}{\lambda _1} = {k_2}\lambda \\ \Rightarrow \lambda = \dfrac{{{k_1}{\lambda _1}}}{{{k_2}}} = \dfrac{{4.0,76}}{{{k_2}}} = \dfrac{{3,04}}{{{k_2}}}\left( {\mu m} \right)\end{array}\)
Lại có:
\(\begin{array}{l}0,38\mu m \le \lambda \le 0,76\mu m\\ \Leftrightarrow 0,38 \le \dfrac{{3,04}}{k} \le 0,76\\ \Leftrightarrow 4 \le k \le 8\\ \Rightarrow k = 4,5,6,7,8\end{array}\)
Vậy trên kính ảnh của buồng tối máy quang phổ này quan sát được năm vạch sáng riêng lẻ (gồm cả của bức xạ có bước sóng \(0,76\mu m\))
Trong thí nghiệm Y-âng về giao thoa ánh sáng. Hai khe được chiếu sáng bởi ánh sáng trắng có bước sóng 0,38μm ≤ λ ≤ 0,76μm. Tại vị trí M trên màn quan sát có một số vân sáng của các bức xạ đơn sắc trùng nhau. Trong số đó có vân sáng bậc n của bức xạ λ1 = 0,6μm, vân sáng bậc n + 1 của bức xạ λ2 = 0,5μm. Tại M còn có số bức xạ khác cho vân sáng là
-
A
2
-
B
1
-
C
4
-
D
3
Đáp án của giáo viên lời giải hay : A
Sử dụng lí thuyết về giao thoa sóng ánh sáng, điều kiện để một điểm là vị trí vân sáng
Vị trí vân sáng: \({x_s} = \frac{{k\lambda D}}{a}\)
+ Tại M là vị trí vân sáng bậc n của λ1 và bậc n + 1 của λ2 => nλ1 = (n +1)λ2
Hay 0,6n = 0,5(n + 1) => n = 5. Khi đó xM = 5i1
+ M còn là vị trí vân sáng của một số bức xạ khác => xM = ki = 5i1 => λ = 5λ1/k
Theo đề bài 0,38μm ≤ λ ≤ 0,76μm => 0,38μm ≤ 5λ1/k ≤ 0,76μm => 3,95 ≤ k ≤ 7,89
Do đó k: 4,5,6,7 => có tất cả 4 bức xạ cho vân sáng tại M
=> Ngoài λ1 và λ2 thì tại M còn 2 bức xạ cho vân sáng
Trong thí nghiệm Y – âng về giao thoa ánh sáng , ánh sáng trắng chiếu vào khe S có bước sóng từ 415nm đến 760nm . M là một điểm trên màn giao thoa, ở đó có đúng 4 bức xạ cho vân sáng và một trong bốn bức xạ đó là bức xạ màu vàng có bước sóng 580nm. Ở M là vân sáng bậc mấy của bức xạ màu vàng nói trên ?
-
A
5
-
B
3
-
C
6
-
D
4
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về giao thoa với ánh sáng trắng
Hai bức xạ trùng nhau: x1 = x2 <=> k1.λ1 = k2.λ2
Vị trí điểm M: \({x_M} = \frac{{k\lambda D}}{a} = \frac{{{k_v}{\lambda _v}D}}{a} \Leftrightarrow k\lambda = {k_v}{\lambda _v} \to \lambda = \frac{{{k_v}{\lambda _v}}}{k} = \frac{{{k_v}.580}}{k}nm\)
\(415nm \le \lambda \le 760nm \Leftrightarrow 415 \le \frac{{415nm \le \lambda \le 760nm.580}}{k} \le 760 \Leftrightarrow \frac{{{k_v}}}{{\frac{{38}}{{29}}}} \le k \le \frac{{{k_v}}}{{\frac{{83}}{{116}}}}\)
\( \Rightarrow \left[ \begin{array}{l}{k_v} = 3 \Rightarrow k = 3;4(L)\\{k_v} = 4 \Rightarrow k = 4;5(L)\\{k_v} = 5 \Rightarrow k = 4;5;6(L)\\{k_v} = 6 \Rightarrow k = 5;6;7;8(C)\end{array} \right.\)
Vậy M là vân sáng bậc 6 của bức xạ màu vàng
Trong thí nghiệm giao thoa ánh sáng dùng khe I-âng, khoảng cách 2 khe a = 1mm, khoảng cách hai khe tới màn D = 2m. Chiếu bằng ánh sáng trắng có bước sóng thỏa mãn 0,39μm \( \le \)λ\( \le \) 0,76μm. Khoảng cách gần nhất từ nơi có hai vạch màu đơn sắc khác nhau trùng nhau đến vân sáng trung tâm ở trên màn là
-
A
3,24mm
-
B
2,34mm
-
C
2,4 mm
-
D
1,64 mm
Đáp án của giáo viên lời giải hay : B
Sử dụng lí thuyết về giao thoa ánh sáng trắng và công thức xác định vị trí vân sáng
Hai vân sáng trùng nhau : x1 = x2 <=> k1.λ1 = k2.λ2
Ở vị trí gần vạch trung tâm nhất mà 2 vạch màu đơn sắc khác nhau trùng nhau, ta có vạch tím thứ n + 1 trùng với vạch màu nào đó thứ n, ta gọi bước sóng của vạch màu đó là λ.
Ta có \({n_t}{i_t} = ni \Leftrightarrow (n + 1){\lambda _t} = n\lambda \Leftrightarrow \lambda = \frac{{n + 1}}{n}{\lambda _t}\) \((n \in \mathbb{N})\)
Có \(0,39 \le \lambda \le 0,76 \Leftrightarrow 0,39 \le \frac{{n + 1}}{n}{\lambda _t} \le 0,76 \Leftrightarrow n \ge 1,054\)
Ta cần tìm n nhỏ nhất nên suy ra \(n = 2 \Rightarrow x = (n + 1){i_t} = (n + 1)\frac{{{\lambda _t}D}}{a} = 2,34(mm)\).
Tiến hành thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát ra đồng thời hai ánh sáng đơn sắc có bước sóng l1 và l2. Trên màn, trong khoảng giữa hai vị trí có vân sáng trùng nhau liên tiếp có tất cả N vị trí mà ở mỗi vị trí đó có một bức xạ cho vân sáng. Biết l1 và l2 có giá trị nằm trong khoảng từ \(400 nm\) đến \(750 nm\). N không thể nhận giá trị nào sau đây?
-
A
\(7\)
-
B
\(8\)
-
C
\(5\)
-
D
\(6\)
Đáp án của giáo viên lời giải hay : B
Giả sử \({\lambda _1} < {\lambda _2}\).
Gọi số vân sáng của lamda1 giữa 2 vân sáng chung liên tiếp là \(n_1\) số vân sáng của \(\lambda_2\) giữa 2 vân sáng chung liên tiếp là \(n_2\)
Ta có N = n1 + n2 và \(({n_1} + 1){\lambda _1} = ({n_2} + 1){\lambda _2} \Rightarrow \dfrac{{{n_1} + 1}}{{{n_2} + 1}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}}\)(1)
Mặt khác, vì \(\lambda_1\) và \(\lambda_2\) trong khoảng \(400nm\) đến \(750nm\) nên \(\dfrac{{{\lambda _2}}}{{{\lambda _1}}} < \dfrac{{750}}{{400}} = 1,875\)(2)
Từ (1) và (2) suy ra \({n_2} < {n_1} < 1,875{n_2} + 0,875\)
Để ý thấy (n1 + 1) và (n2 + 1) phải là 2 số nguyên tố cùng nhau (UCLN phải bằng 1) để giữa 2 vân sáng chung không còn vân sáng chung nào khác. Ta có bảng sau:
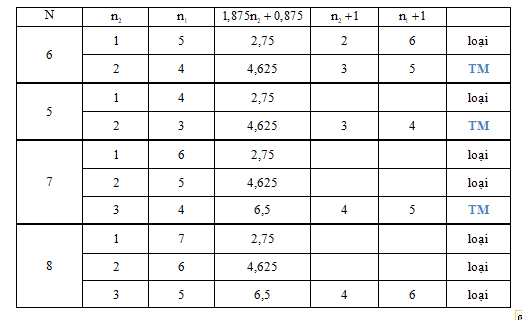
Vậy ta thấy với N = 8 thì không có giá trị nào thỏa mãn đề bài
