Một học sinh làm thí nghiệm Y – âng về giao thoa ánh sáng để đo bước sóng ánh sáng. Khoảng cách hai khe sáng là \(1,00{\rm{ }} \pm {\rm{ }}0,05{\rm{ }}\left( {mm} \right)\). Khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \(2,00{\rm{ }} \pm {\rm{ }}0,01{\rm{ }}\left( m \right)\); khoảng cách giữa \(10\) vân sáng liên tiếp đo được là \(10,80{\rm{ }} \pm {\rm{ }}0,14{\rm{ }}\left( {mm} \right)\). Bước sóng bằng:
-
A
\(0,54{\rm{ }} \pm {\rm{ }}0,03{\rm{ }}\left( {\mu m} \right)\)
-
B
\(0,54{\rm{ }} \pm {\rm{ }}0,04{\rm{ }}\left( {\mu m} \right)\)
-
C
\(0,60{\rm{ }} \pm {\rm{ }}0,03{\rm{ }}\left( {\mu m} \right)\)
-
D
\(0,60{\rm{ }} \pm {\rm{ }}0,04{\rm{ }}\left( {\mu m} \right)\)
Đáp án của giáo viên lời giải hay : D
+ Khoảng cách giữa \(n\) vân sáng liên tiếp là: \(\left( {n - 1} \right)i\)
+ Sử dụng công thức tính bước sóng: \(\lambda = \frac{{ai}}{D}\)
+ Sử dụng công thức tính sai số trong thực hành thí nghiệm: \(\frac{{\Delta \lambda }}{\lambda } = \frac{{\Delta a}}{a} + \frac{{\Delta i}}{i} + \frac{{\Delta D}}{D}\)
+ Khoảng cách giữa \(10\) vân sáng liên tiếp bằng \(9i\), ta có: \(9.\bar i{\rm{}} = 10,80 \pm 0,14mm \Rightarrow \bar i{\rm{}} = 1,2 \pm \frac{{0,14}}{9}mm\)
+ Bước sóng: \(\bar \lambda {\rm{ }} = \frac{{\bar a.\bar i}}{{\bar D}} = \frac{{1.1,2}}{2} = 0,6\mu m\)
Sai số:
\(\begin{array}{l}\frac{{\Delta \lambda }}{\lambda } = \frac{{\Delta a}}{a} + \frac{{\Delta i}}{i} + \frac{{\Delta D}}{D}\\ \to \Delta \lambda = \overline \lambda \left( {\frac{{\Delta a}}{{\overline a }} + \frac{{\Delta i}}{{\overline i }} + \frac{{\Delta D}}{{\overline D }}} \right)\\ = 0,6\left( {\frac{{0,05}}{1} + \frac{{\frac{{0,14}}{9}}}{{1,2}} + \frac{{0,01}}{2}} \right) = 0,04\mu m\end{array}\)
=> Bước sóng bằng: \(0,60{\rm{ }} \pm {\rm{ }}0,04{\rm{ }}\mu m\)
Trong thí nghiệm Y – âng về giao thoa ánh sáng, khe hẹp S phát ra đồng thời 3 bức xạ đơn sắc có bước sóng là \({\lambda _1} = {\rm{ }}0,42\mu m\) , \({\lambda _2} = {\rm{ }}0,56\mu m\) và \({\lambda _3} = {\rm{ }}0,63\mu m\) . Trên màn, trong khoảng giữa hai vân sáng liên tiếp có màu giống vân trung tâm, nếu vân sáng của hai bức xạ trùng nhau ta chỉ tính là một vân sáng thì số vân sáng quan sát được:
-
A
26
-
B
21
-
C
27
-
D
23
Đáp án của giáo viên lời giải hay : B
Sử dụng lí thuyết về giao thoa ánh sáng
+ Sử dụng điều kiện của các bức xạ trùng nhau: \({k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3}\)
+ Xác định số vân sáng trùng nhau của các cặp bước sóng
+ Xác định số vân sáng quan sát được trên màn
- Vị trí trùng nhau của 3 bức xạ:
\(\begin{array}{l}{x_1} = {x_2} = {x_3} \Rightarrow {k_1}.0,42 = {k_2}.0,56 = {k_3}.0,63 \Rightarrow 6{k_1} = 8{k_2} = 9{k_3}\\BCNN(6;8;9) = 72 \Rightarrow {k_1}:{k_2}:{k_3} = 12:9:8 \Rightarrow \left\{ \begin{array}{l}{k_1} = 12n\\{k_2} = 9n\\{k_3} = 8n\end{array} \right.\end{array}\)
Trong khoảng giữa hai vân sáng cùng màu với vân trung tâm có \(11\) vân sáng của bức xạ \(1\) ; \(8\) vân sáng của bức xạ \(2\) và \(7\) vân sáng của bức xạ \(3\)
- Số vân sáng trùng nhau của \({\lambda _1}\) và \({\lambda _2}\): \({k_1}{\lambda _1} = {k_2}{\lambda _2} \Rightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{0,56}}{{0,42}} = \frac{4}{3} \Rightarrow \left\{ \begin{array}{l}{k_1} = 4.{n_1}\\{k_2} = 3{n_1}\end{array} \right.\)
=> Trong khoảng giữa hai vân sáng liên tiếp có màu giống vân trung tâm có \(2\) vân trùng nhau của \({\lambda _1}\) và \({\lambda _2}\) (ứng với \({n_1} = 1;2\))
- Số vân sáng trùng nhau của \({\lambda _1}\) và \({\lambda _3}\): \({k_1}{\lambda _1} = {k_3}{\lambda _3} \Rightarrow \frac{{{k_1}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _1}}} = \frac{{0,63}}{{0,42}} = \frac{3}{2} \Rightarrow \left\{ \begin{array}{l}{k_1} = 3{n_2}\\{k_3} = 2{n_2}\end{array} \right.\)
=> Trong khoảng giữa hai vân sáng liên tiếp có màu giống vân trung tâm có \(3\) vân trùng nhau của \({\lambda _1}\) và \({\lambda _2}\) (ứng với \({n_2} = 1;2;3\) )
- Số vân sáng trùng nhau của \({\lambda _2}\) và \({\lambda _3}\): \({k_2}{\lambda _2} = {k_3}{\lambda _3} \Rightarrow \frac{{{k_2}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _2}}} = \frac{{0,63}}{{0,56}} = \frac{9}{8} \Rightarrow \left\{ \begin{array}{l}{k_2} = 9{n_3}\\{k_3} = 8{n_3}\end{array} \right.\)
=> Trong khoảng giữa hai vân sáng liên tiếp có màu giống vân trung tâm không có vân trùng nhau của \({\lambda _2}\) và \({\lambda _3}\)
- Vân sáng của hai bức xạ trùng nhau ta chỉ tính là \(1\)
=> Số vân sáng quan sát được: \(N{\rm{ }} = {\rm{ }}11{\rm{ }} + {\rm{ }}8{\rm{ }} + {\rm{ }}7{\rm{ }}-{\rm{ }}5{\rm{ }} = {\rm{ }}21\)
Thực hiện giao thoa khe Y-âng với hai bức xạ đơn sắc \({\lambda _1}\) và \({\lambda _2}\) thì khoảng vân tương ứng là \({i_1} = {\rm{ }}0,3{\rm{ }}mm\) và \({i_2} = {\rm{ }}0,4{\rm{ }}mm\) . Gọi \(A\) và \(B\) là hai điểm trên màn quan sát, nằm cùng một phía so với vân trung tâm và cách nhau \(3mm\). Biết tại \(A\) là vị trí vân sáng trùng nhau của hai bức xạ, nếu vị trí vân sáng trùng nhau chỉ tính một vân sáng thì số vân sáng quan sát được trên đoạn \(AB\) (kể cả \(A\) và \(B\)) là:
-
A
15
-
B
18
-
C
17
-
D
16
Đáp án của giáo viên lời giải hay : D
Sử dụng lí thuyết bài toán giao thoa nhiều ánh sáng
+ Số vân sáng của bức xạ đơn sắc 1 thu được trên màn \({N_1} = 2\left[ {\dfrac{L}{{2{i_1}}}} \right] + 1 = 11\)
+ Số vân sáng của bức xạ đơn sắc 2 thu được trên màn \({N_2} = 8\) (Tính cả vị trí tại A vì tại đó bức xạ 1 và 2 cùng cho vân sáng)
+ Xét sự trùng nhau của hai bức xạ \(\dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{i_2}}}{{{i_1}}} = \dfrac{4}{3} \Rightarrow {x_{tr}} = 4{i_1} = 3{i_2} = 1,2mm\)
+ Số vân sáng trùng nhau của hai bức xạ là \({N_{tr}} = 2\left[ {\dfrac{L}{{2{x_{tr}}}}} \right] + 1 = 3\)
Vẽ trên hình ta được:
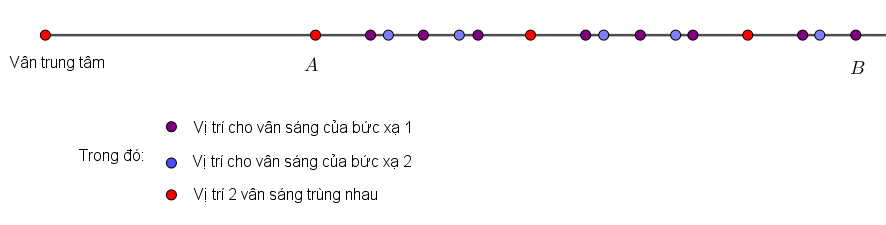
=> Số vân sáng quan sát được trên màn là: \(N=N_1+N_2-N_{tr}=11+8-3=16\) vân sáng
Trong thí nghiệm Young về giao thoa ánh sáng, nguồn S phát ra đồng thời ba bức xạ đơn sắc có bước sóng lần lượt là \(0,4{\rm{ }}\mu m\) ; \(0,5{\rm{ }}\mu m\) và \(0,6{\rm{ }}\mu m\). Trên màn, trong khoảng giữa hai vân sáng liên tiếp cùng màu với vân sáng trung tâm, có bao nhiêu vị trí mà ở đó chỉ có một bức xạ cho vân sáng:
-
A
18
-
B
20
-
C
22
-
D
26
Đáp án của giáo viên lời giải hay : B
+ Áp dụng điều kiện trùng nhau của các vân sáng trong giao thoa sóng ánh sáng: \({k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3}\)
+ Xác định vị trí trùng nhau của các cặp bức xạ
Vị trí trùng màu với vân trung tâm là vị trí trùng nhau của vân sáng \(3\) bức xạ: \({x_1} = {\rm{ }}{x_2} = {\rm{ }}{x_3} \leftrightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3} = > 4{k_1} = {\rm{ }}5{k_2} = 6{k_3}\)
→ Vị trí trùng nhau gần vân trung tâm nhất ứng với \({k_1} = {\rm{ }}15,{\rm{ }}{k_2} = {\rm{ }}12\) và \({k_{3}} = {\rm{ }}10\)
+ Sự trùng nhau của hai bức xạ \({\lambda _1}\) và \({\lambda _2}\) trong khoảng này: \({x_1} = {x_2} \leftrightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{5}{4}\)
→ có \(2\) vị trí trùng nhau của hai hệ vân ứng với \({k_1} = 5,10\)
+ Sự trùng nhau của hai bức xạ \({\lambda _1}\) và \({\lambda _3}\) trong khoảng này: \({x_1} = {x_3} \leftrightarrow \frac{{{k_1}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _1}}} = \frac{3}{2}\)
→ có \(4\) vị trí trùng nhau của hai hệ vân ứng với \({k_1} = 3,6, 9\) và \(12\)
+ Sự trùng nhau của hai bức xạ \({\lambda _2}\) và \({\lambda _3}\) trong khoảng này: \({x_2} = {x_3} \leftrightarrow \frac{{{k_2}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _2}}} = \frac{6}{5}\)
→ có \(1\) vị trí trùng nhau của hai hệ vân ứng với \({k_2} = 6\)
Vậy số vị trí cho vân đơn sắc là: \(14{\rm{ }} + {\rm{ }}11{\rm{ }} + {\rm{ }}9{\rm{ }}-{\rm{ }}2.2{\rm{ }}-{\rm{ }}2.4{\rm{ }}-{\rm{ }}2.1{\rm{ }} = {\rm{ }}20\)
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn phát ra ánh sáng trắng có bước sóng từ \(380nm\) đến \(760nm\). Trên màn quan sát, tại điểm \(M\) có đúng \(4\) bức xạ cho vân sáng có bước sóng \(390nm\); \(520nm\);\({\lambda _1}\) và \({\lambda _2}\). Tổng giá trị gần nhất với:
-
A
\(10000nm\)
-
B
\(890nm\)
-
C
\(1069nm\)
-
D
\(943nm\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng điều kiện vân sáng trùng nhau: \({k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3}\)
+ Sử dụng biểu thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
+ Sử dụng điều kiện chồng chập vân: \({x_{{d_{\left( k \right)}}}} > {x_{{t_{\left( {k + 1} \right)}}}}\)
Tại M có cùng lúc 4 vân sáng ứng với 4 bức xạ, nên ta có :
\(\begin{array}{*{20}{l}}{{x_M} = {k_1}.{i_1} = {k_2}.{i_2} = {k_3}.{i_3} = {k_4}.{i_4}}\\{ = > \frac{{{k_3}}}{{{k_4}}} = \frac{{{i_4}}}{{{i_3}}} = \frac{{{\lambda _4}}}{{{\lambda _3}}} = \frac{{520}}{{390}} = \frac{4}{3}}\end{array}\)
Ta có thể coi như ở đây có sự giao thoa của hệ vân mà khoảng vân bằng bội của \(4.{i_3}\) hoặc \(3{i_4}\) .
Tức là :
\(\begin{array}{*{20}{l}}{i' = 4.\frac{{{\lambda _3}.D}}{a} = 4.390.x = 1560x}\\{Khi(x = \frac{D}{a})}\end{array}\)
Điều kiện để có hai dải vân chồng chập lên nhau là :
\(\begin{array}{l}{x_{{d_{\left( k \right)}}}} > {x_{{t_{\left( {k + 1} \right)}}}}\\ \leftrightarrow k{i_d} > \left( {k + 1} \right){i_t}\\ \leftrightarrow k{\lambda _d} > \left( {k + 1} \right){\lambda _t}\end{array}\)
\(\begin{array}{*{20}{l}}{k.760 > (k + 1).380}\\{ = > k > 1}\end{array}\)
Xét với \(k{\rm{ }} = {\rm{ }}2\), thì:
\(i' = 2.4{i_3} = 8{i_3} = 2.3{i_4} = 6{i_4} = 3120x\)
Ta lập bảng để xét các giá trị thỏa mãn:
![]()
Vậy chọn các giá trị ứng với \(k{\rm{ }} = {\rm{ }}8,7,6,5\)
Thì \({\lambda _1} + {\lambda _2} = 624 + 445,71 \approx 1069nm\)
Thí nghiệm giao thoa ánh sáng đơn sắc với hai khe \({S_1},{S_2}\) như hình vẽ.
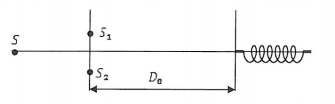
Màn quan sát gắn với lò xo và có thể dao động điều hòa với chu kì riêng \(T{\rm{ }} = {\rm{ }}1,5s\). Bỏ qua ma sát và sức cản môi trường. ban đầu màn nằm cân bằng và khoảng cách từ hai khe đến màn là \({D_0}\) ta thu được một hệ vân giao thoa mà điểm M trên màn cách vân sáng trung tâm \(3\left( {mm} \right)\) là vân sáng bậc \(3\). Đưa màn đến vị trí lò xo nén \(\Delta l = \dfrac{{{D_0}}}{{\sqrt 2 }}\) rồi thả nhẹ cho dao động. Sau bao lâu thì tại M ta thu được vân sáng bậc \(2\) lần đầu:
-
A
\(\dfrac{1}{{16}}s\)
-
B
\(\dfrac{3}{7}s\)
-
C
\(\dfrac{1}{{11}}s\)
-
D
\(\dfrac{3}{{16}}s\)
Đáp án của giáo viên lời giải hay : D
Sử dụng công thức xác định vị trí vân sáng: \({x_S} = ki = k\dfrac{{\lambda D}}{a}\)
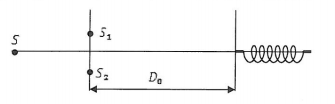
Ban đầu khoảng cách từ 2 khe đến màn quan sát là \({D_0}\) thì tại M cách vân trung tâm 3mm là vân sáng bậc 3 nên ta có \({x_M} = k\frac{{\lambda {D_0}}}{a} = 3.\frac{{\lambda {D_0}}}{a}\) (1)
Vì đây là con lắc lò xo nằm ngang nên khi đưa màn quan sát đến vị trí lò xo bị nén \(\Delta l = \frac{{{D_0}}}{{\sqrt 2 }}\) rồi buông nhẹ thì ta cũng có \(A = \frac{{{D_0}}}{{\sqrt 2 }}\)
Khi M là vân sáng bậc 2 thì gọi D là khoảng cách từ 2 khe đến màn quan sát ta có: \({x_M} = k\frac{{\lambda D}}{a} = 2.\frac{{\lambda D}}{a}\) (2)
Từ (1) và (2) ta có: \(3\frac{{\lambda {D_0}}}{a} = 2\frac{{\lambda D}}{a} \Leftrightarrow D = \frac{3}{2}{D_0}\)
Khoảng thời gian từ thời điểm thả nhẹ màn cho dao động đến khi M trở thành vân sáng bậc 2 lần đầu chính là khoảng thời gian ngắn nhất để màn dao động từ biên độ A đến điểm B tức là khi đó màn dao động từ biên đến vị trí cách vị trí cân bằng 1 khoảng \(\frac{{\sqrt 2 }}{2}A\) nên ta có \(t = \frac{T}{8} = \frac{{1,5}}{8} = \frac{3}{{16}}s\)
Trong thí nghiệm giao thoa ánh sáng bằng khe Y-âng. Ánh sáng sử dụng gồm 3 bức xạ đơn sắc đỏ, lục và lam có bước sóng lần lượt là \({\lambda _1} = {\rm{ }}0,64\mu m\) , \({\lambda _2} = {\rm{ }}0,54\mu m\) , \({\lambda _3} = {\rm{ }}0,48{\rm{ }}\mu m\). Trong khoảng giữa hai vân liên tiếp có màu của vân trung tâm O có bao nhiêu vạch sáng có màu đơn sắc?
-
A
92
-
B
70
-
C
81
-
D
80
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về bài toán trùng nhau của 3 bức xạ trong giao thoa sóng ánh sáng: \({k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3}\)
+ Giả sử M là vị trí trung nhau của ba bức xạ =>\({x_M} = {k_1}{i_1} = {k_2}{i_2} = {k_3}{i_3} < = > 64{k_1} = 54{k_2} = 48{k_3}\)
+ BCNN(64;54;48) = 1728
=> VT trùng nhau đầu tiên là vị trí ứng với \({k_1} = {\rm{ }}27,{\rm{ }}{k_2} = {\rm{ }}32,{\rm{ }}{k_3} = {\rm{ }}36\)
+ Xét sự trùng nhau của hai bức xạ:
- Bức xạ đơn sắc đỏ và lục: \(\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{0,54}}{{0,64}} = \frac{{27}}{{32}} = > {k_1} = 27,{k_2} = 32\)
=> Trong khoảng giữa hai vân sáng cùng màu với vân trung tâm không có sự trùng nhau của đỏ và lục
- Bức xạ đơn sắc lục và làm :\(\frac{{{k_2}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _2}}} = \frac{{0,48}}{{0,54}} = \frac{8}{9} = > {k_2} = 8,{k_3} = 9\) => Khoảng vân trùng nhau của lục và làm là \({i_{C23}} = 8{i_2} = 9{i_3}\)
=> Trong khoảng giữa hai vân sáng cùng màu với vân trung tâm có 3 vị trí trùng nhau của lục và lam
- Bức xạ đơn sắc đỏ và lam: \(\frac{{{k_1}}}{{{k_3}}} = \frac{{{\lambda _3}}}{{{\lambda _1}}} = \frac{{0,48}}{{0,64}} = \frac{3}{4} = > {k_1} = 3,{k_3} = 4\) => Khoảng vân trùng nhau của đỏ và lam là \({i_{C31}} = 3{i_1} = 4{i_3}\)
=> Trong khoảng giữa hai vân sáng trùng màu với vân trung tâm có 8 vị trí trùng nhau của đỏ và lam
Như vậy tổng số vân sáng đơn sắc quan sát được trong khoảng giữa hai vân có màu trùng màu với vân trung tâm là \(N{\rm{ }} = {\rm{ }}26{\rm{ }} + {\rm{ }}31{\rm{ }} + {\rm{ }}35{\rm{ }}-{\rm{ }}3{\rm{ }}-{\rm{ }}8{\rm{ }} = {\rm{ }}81\) (vân)
Đặt một khối chất trong suốt có 2 mặt song song, bề dầy \(e =2cm\) trong không khí. Từ không khí chiếu một chùm sáng hỗn hợp gồm 2 ánh sáng đơn sắc \({\lambda _1}\) và \({\lambda _2}\) coi như một tia sáng tới mặt trên khối chất dưới góc tới \(i = {60^0}\) như hình vẽ bên. Biết chiết suất của khối chất đó đối với ánh sáng \({\lambda _1}\) và \({\lambda _2}\) lần lượt là \({n_1} = \sqrt 3 \) và \({n_2} = \sqrt 2 \). Khoảng cách giữa 2 tia ló ra ở mặt dưới của khối chất là:
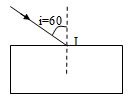
-
A
1,549cm
-
B
0,197cm
-
C
0,394cm
-
D
1,155cm
Đáp án của giáo viên lời giải hay : B
Định luật khúc xạ ánh sáng \({n_1}sini{\rm{ }} = {\rm{ }}{n_2}sinr\)
Theo định luật khúc xạ ánh sáng ta vẽ được đường đi qua khối chất trong suốt trên của tia sáng như hình vẽ.
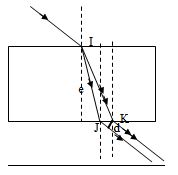
Dễ thấy sau khi bị tán sắc ở mặt trên và ló ra ở mặt dưới của khối chất thì 2 tia đơn sắc \({\lambda _1}\) và \({\lambda _2}\) song song với nhau.
Từ hình vẽ ta có khoảng cách giữa 2 tia ló là:
\(d = JK.sin\left( {90 - i} \right) = e.\left( {tan{r_2} - tan{r_1}} \right).sin\left( {90 - i} \right)\left( 1 \right)\)
Với \(i = {60^0}\); \({r_2} = \arcsin \left( {\dfrac{{{\rm{sini}}}}{{{{\rm{n}}_{\rm{2}}}}}} \right) = {\rm{ }}arcsin\left( {\dfrac{{{\rm{sin 60}}}}{{\sqrt 2 }}} \right)\); \({r_1} = arcsin\left( {\dfrac{{{\rm{sin 60}}}}{{\sqrt 3 }}} \right)\); \(e{\rm{ }} = {\rm{ }}2cm\) ;
Thay vào (1) ta được: \(d = {\rm{ }}0,1972cm\)
Chiếu một chùm sáng hẹp tới mặt trên của một chậu nước dưới góc tới \(i = {60^0}\) chiết suất của nước với ánh sáng đỏ và tím là \({n_d} = 1,31\) ; \({n_t} = 1,38\). Độ sâu của lớp nước là \(30cm\), đáy chậu đặt một gương phẳng nằm ngang, bề rộng dải quang phổ liên tục thu được ở ngoài không khí:
-
A
4,5cm
-
B
2,25cm
-
C
2,25m
-
D
5,4cm
Đáp án của giáo viên lời giải hay : B
Sử dụng lí thuyết về tán sắc ánh sáng
Định luật khúc xạ ánh sáng: \({n_1}sini{\rm{ }} = {\rm{ }}{n_2}sinr\)
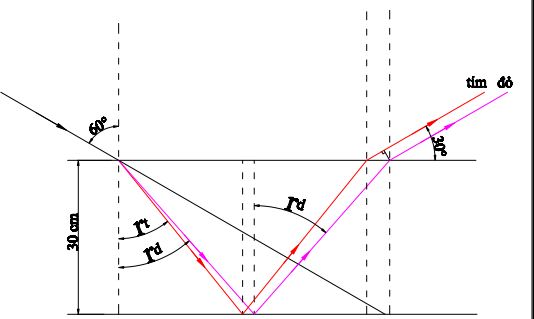
Áp dụng định luật khúc xạ ánh sáng ta tính được
\(sini = {n_d}sin{\rm{ }}{r_d} \to sin{\rm{ }}{r_d} = \frac{{sin{\rm{ }}i}}{{{n_d}}} = \frac{{sin{\rm{ }}{{60}^0}}}{{1,31}} \to {r_d} = {41,38^0}\)
\(sin{\rm{ }}i = {n_t}sin{\rm{ }}{r_t} \to sin{\rm{ }}{r_t} = {\rm{ }}\frac{{sin{\rm{ }}i}}{{{n_t}}}{\rm{ = }}\frac{{sin{\rm{ }}{{60}^0}}}{{1,38}} \to {\rm{ }}{r_t} = {\rm{ }}{38,87^0}\)
Từ hình vẽ trên ta thấy:
Bề rộng quang phổ tại mặt nước được tính theo công thức: \(L = 2h\left( {tan{\rm{ }}{r_d}-{\rm{ }}tan{\rm{ }}{r_t}} \right) = 4,5{\rm{ }}cm\)
=> Bề rộng quang phổ trong không khí là \(d{\rm{ }} = {\rm{ }}Lsin{\rm{ }}{30^0} = {\rm{ }}2,25cm\)
Trong một thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là \(2mm\), khoảng cách từ hai khe đến màn quan sát là \(2m\). Nguồn sáng gồm hai bức xạ có bước sóng \({\lambda _1} = {\rm{ }}0,5{\rm{ }}\mu m\) và \({\lambda _2} = {\rm{ }}0,4{\rm{ }}\mu m\) . Trên bề rộng trường giao thoa \(L{\rm{ }} = {\rm{ }}13mm\), số vân sáng quan sát được là:
-
A
53
-
B
60
-
C
67
-
D
30
Đáp án của giáo viên lời giải hay : A
+ Sử dụng lí thuyết về giao thoa đồng thời hai nguồn đơn sắc
+ Vị trí vân sáng \({x_s} = {\rm{ }}ki\)
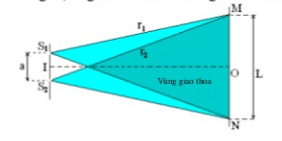
\({i_1} = \dfrac{{d{\lambda _1}}}{a} = 0,5mm,{i_2} = \dfrac{{d{\lambda _2}}}{a} = 0,4mm\)
\(\dfrac{{{k_2}}}{{{k_1}}} = \dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{5}{4}\)
\( \Rightarrow {i_{12}} = 4{i_1} = 2mm\)
Xét: \(\dfrac{L}{{2{i_1}}} = 13 \Rightarrow \) từ trung tâm tới M có 13 vân sáng của bức xạ 1 (không tính vân trung tâm)
\(\dfrac{L}{{2{i_2}}} = 16,25 \Rightarrow \) từ trung tâm tới M có 16 vân sáng của bức xạ 2 (không tính vân trung tâm)
\(\dfrac{L}{{2{i_{12}}}} = 3,25 \Rightarrow \) từ trung tâm tới M có 3 vân sáng trùng màu nhau (không tính vân trung tâm)
Suy ra từ trung tâm tới M có \(13 + 16 - 3 = 26\) vân sáng (không tính vân trung tâm)
Vậy trên màn có \(26.2 + 1 = 53\) vân sáng
Thực hiện thí nghiệm giao thoa Y – âng với ánh sáng đơn sắc có bước sóng \(560nm\). Khoảng cách giữa hai khe S1S2 là \(1mm\). Khoảng cách từ mặt phẳng chứa hai khe đến màn là \(2,5m\). Goi M và N là hai điêmt trên trường giao thoa, cách vân sáng trung tâm lần lượt là \(107,25mm\) và \(82,5mm\). Lúc \(t = 0\) bắt đầu cho màn dịch chuyển thẳng đều theo phương vuông góc với mặt phẳng chứa hai khe và ra xa S1S2 với tốc độ \(5cm/s\). Gọi t1 là thời điểm đầu tiên mà tại M và N đồng thời cho vân sáng. Gọi t2 là thời điểm đầu tiên mà tại M cho vân tối, đồng thời tại N cho vân sáng. Khoảng thời gian \(\Delta t = \left| {{t_1} - {t_2}} \right|\) có giá trị gần nhất với giá trị nào sau đây ?
-
A
3,4s
-
B
2,7s
-
C
5,4s
-
D
6,5s
Đáp án của giáo viên lời giải hay : C
+ Vị trí vân sáng và vân tối : \(\left\{ \begin{array}{l}{x_s} = ki = k\dfrac{{\lambda D}}{a}\\{x_t} = \left( {k + \dfrac{1}{2}} \right)i = \left( {k + \dfrac{1}{2}} \right).\dfrac{{\lambda D}}{a}\end{array} \right.\)
+ Công thức liên hệ giữa S, v và t : \(S = v.t\)
+ Lúc \(t = 0\) bắt đầu cho màn dịch chuyển thẳng đều theo phương vuông góc với mặt phẳng chứa hai khe và ra xa S1S2 với tốc độ \(5cm/s\)
+ t1 là thời điểm đầu tiên mà tại M và N đồng thời cho vân sáng. Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{x_M} = 107,25 = \dfrac{{{k_1}.0,56.\left( {2,5 + 0,05.{t_1}} \right)}}{1}\\{x_N} = 82,5 = \dfrac{{{k_1}'.0,56.\left( {2,5 + 0,05.{t_1}} \right)}}{1}\end{array} \right. \Rightarrow \dfrac{{{x_M}}}{{{x_N}}} = \dfrac{{{k_1}}}{{{k_1}'}} = \dfrac{{107,25}}{{82,5}} = 1,3\\ \Rightarrow \left\{ \begin{array}{l}{k_1} = 65\\{k_1}' = 50\end{array} \right. \Rightarrow {t_1} = \dfrac{{125}}{{14}}\left( s \right)\end{array}\)
+ t2 là thời điểm đầu tiên mà tại M cho vân tối, đồng thời tại N cho vân sáng.
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{x_M} = 107,25 = \left( {{k_2} + \dfrac{1}{2}} \right).\dfrac{{0,56.\left( {2,5 + 0,05.{t_2}} \right)}}{1}\\{x_N} = 82,5 = {k_2}'.\dfrac{{0,56.\left( {2,5 + 0,05.{t_2}} \right)}}{1}\end{array} \right. \Rightarrow \dfrac{{{x_M}}}{{{x_N}}} = \dfrac{{{k_2} + \dfrac{1}{2}}}{{{k_2}'}} = \dfrac{{107,25}}{{82,5}} = 1,3\\ \Rightarrow \left\{ \begin{array}{l}{k_2} + \dfrac{1}{2} = 71,5\\{k_2}' = 55\end{array} \right. \Rightarrow {t_2} = \dfrac{{25}}{7}\left( s \right)\end{array}\)
=> Khoảng thời gian \(\Delta t = \left| {{t_1} - {t_2}} \right| = \left| {\dfrac{{125}}{{14}} - \dfrac{{25}}{7}} \right| = \dfrac{{75}}{{14}} = 5,357s\)
Trong thí nghiệm Y‒âng về giao thoa ánh sáng, người ta sử dụng nguồn phát ánh sáng trắng có bước sóng từ \(400 nm\) đến \(760 nm\). Trên màn quan sát, \(M\) là vị trí mà tại đó có đúng \(6\) bức xạ cho vân sáng, trong đó có vân sáng của hai bức xạ có bước sóng là \(680 nm\) và \(544 nm\). Tại \(M\) cũng là vị trí vân tối của một số bức xạ khác trong đó bức xạ có bước sóng ngắn nhất là \({\lambda _{min}}\). Giá trị \({\lambda _{min}}\) gần nhất với giá trị nào sau đây?
-
A
\(403 nm\).
-
B
\(494 nm\).
-
C
\(400 nm\).
-
D
\(463 nm\).
Đáp án của giáo viên lời giải hay : A
Tại vị trí n các vân sáng trùng nhau ,có n giá trị thỏa mãn: \({k_1}{\lambda _1} = k\lambda \)
Tại vị trí cho vân sáng: x=ki
Tại vị trí cho vân tối : x=(m+0,5)i
+ \(\dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}} = \dfrac{{544}}{{680}} = \dfrac{4}{5} = \dfrac{8}{{10}} = \dfrac{{12}}{{15}} = ...\)
+ \({k_1}{\lambda _1} = k\lambda \)
\({k_1} = 4 \to 400 \le \lambda = \dfrac{{{k_1}{\lambda _1}}}{k} = \dfrac{{4.680}}{k} \le 760 \to 3,58 \le k \le 6,8 \to k = 4,5,6(loai)\) \({k_1} = 8 \to 400 \le \lambda = \dfrac{{{k_1}{\lambda _1}}}{k} = \dfrac{{8.680}}{k} \le 760 \to 7,16 \le k \le 13,6(*) \to k = \underbrace {8,9,10,11,12,13}_{co6giatri \to co6bucxa}\)
+ Vị trí M: x=8.i1
+ Tại M cũng là vị trí vân tối của một số bức xạ khác => \(x = 8.{i_1} = (m + \dfrac{1}{2})i' \to \lambda ' = \dfrac{{8.{\lambda _1}}}{{(m + \dfrac{1}{2})}}\)
Mà \(400 \le \lambda ' \le 760 \to 400 \le \dfrac{{8.{\lambda _1}}}{{(m + \dfrac{1}{2})}} \le 760 \to 6,6 \le m \le 13,1\)
à \({\lambda _{\min }} = \dfrac{{8.680}}{{13,5}} \approx \)\(402,962963(nm)\)
