Đề bài
Phần I: Trắc nghiệm (2,0 điểm)
Hãy viết chữ cái đứng trước phương án trả lời đúng vào bài làm
Câu 1. Cặp số \(\left( {x;\,\,y} \right)\) nào dưới đây là một nghiệm của phương trình \(2x - 3y = 5\)?
A. \(\left( {4;\,\, - 1} \right)\) B. \(\left( {1;\,\, - 1} \right)\)
C. \(\left( {1;\,\,1} \right)\) D. \(\left( { - 1;\,\,1} \right)\)
Câu 2. Trong mặt phẳng tọa độ \(Oxy\), số giao điểm của đồ thị hai hàm số \(y = {x^2}\) và \(y = 2x + 3\) là
A. \(0\) B. \(1\)
C. \(2\) D. \(3\)
Câu 3. Hàm số \(y = \left( {m - 1} \right){x^2}\) nghịch biến với \(x > 0\) khi và chỉ khi
A. \(m < 1\) B. \(m > 1\)
C. \(m < 0\) D. \(m > 0\)
Câu 4. Phương trình nào sau đây có nghiệm kép?
A. \({x^2} - 1 = 0\) B. \({x^2} + 2x = 0\)
C. \({x^2} - 2x + 1 = 0\) D. \({x^2} - 3x + 2 = 0\)
Câu 5. Phương trình \(m{x^2} - 2x + 1 = 0\) (\(m\) là tham số) có hai nghiệm phân biệt khi và chỉ khi
A. \(m < 1\) B. \(m < 1\) và \(m \ne 0\)
C. \(m > 1\) D. \(m \ne 0\)
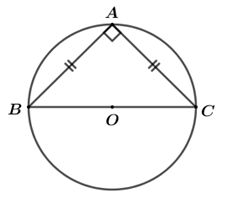
Câu 6. Cho tam giác \(ABC\) vuông cân tại \(A\) nội tiếp đường tròn \(\left( O \right)\). Số đo cung nhỏ \(AC\) bằng
A. \({45^0}\) B. \({270^0}\)
C. \({120^0}\) D. \({90^0}\)
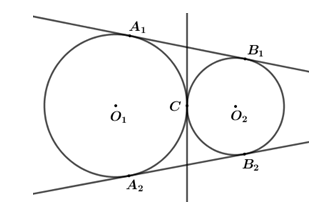
Câu 7. Số tiếp tuyến chung của hai đường tròn tiếp xúc ngoài là
A. \(1\) B. \(2\)
C. \(3\) D. \(4\)
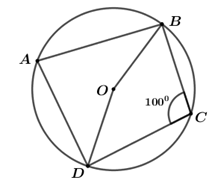
Câu 8. Cho tứ giác \(ABCD\) nội tiếp một đường tròn tâm \(O\) và \(\angle BCD = {100^0}\). Số đo \(\angle DOB\) bằng
A. \({100^0}\) B. \({80^0}\)
C. \({160^0}\) D. \({40^0}\)
Phần II: Tự luận (8,0 điểm)
Câu 1 (1,5 điểm):
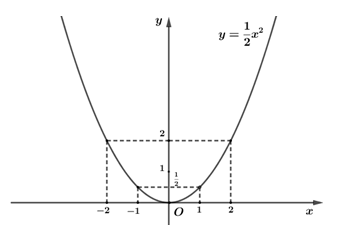
1) Trong mặt phẳng tọa độ \(Oxy\), vẽ đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
2) Trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\) lấy điểm \(A\) có hoành độ bằng \(2\) và điểm \(B\) có tung độ bằng \(2\) (điểm \(B\) khác điểm \(A\)). Hãy viết phương trình đường thẳng \(AB\) và chứng minh \(\Delta OAB\) cân.
Câu 2 (2,0 điểm)
1) Giải hệ phương trình:
\(\left\{ \begin{array}{l}x\left( {x - 3y} \right) + y\left( {y + x} \right) = 0\\\sqrt x .\sqrt {y - 2} = 1\end{array} \right.\)
2) Một hình chữ nhật có chu vi bằng \(28m\), diện tích bằng \(48{m^2}\). Tìm các kích thước của hình chữ nhật đó.
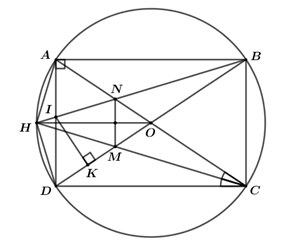
Câu 3 (3,5 điểm): Cho hình chữ nhật \(ABCD\,\,\left( {AB > AD} \right)\) nội tiếp đường tròn tâm \(O\). Tia phân giác \(\angle ACD\) cắt cung nhỏ \(AD\) của đường tròn \(\left( O \right)\) tại điểm \(H\).
1) Chứng minh: Ba điểm \(A,\,\,O,\,\,C\) thẳng hàng và \(HA = HD\)
2) Dây \(HC\) của \(\left( O \right)\) cắt \(BD\) tại \(M\), dây \(HB\) của \(\left( O \right)\) cắt \(AC\) tại \(N\). Chứng minh: Tứ giác\(MNBC\) nội tiếp và \(MN \bot OH\).
3) Dây \(HB\) của \(\left( O \right)\) cắt \(AD\) tại \(I\). Chứng minh \(IA < ID\) và \(AB.AC = BH.BI\).
Câu 4 (1,0 điểm): Cho phương trình: \(\left( {x - 1} \right)\left( {{x^2} + 5mx + 4{m^2}} \right) = 0\,\,\,\,\,\left( 1 \right)\) (với \(m\) là tham số)
Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có đúng hai nghiệm phân biệt.
Lời giải chi tiết
Phần I: Trắc nghiệm
|
1. B |
2. C |
3. A |
4. C |
|
5. B |
6. D |
7. C |
8. B |
Câu 1 (TH):
Phương pháp:
Cặp số \(\left( {{x_0};\,\,{y_0}} \right)\) là nghiệm của phương trình \(ax + by = c\) khi \(a{x_0} + b{y_0} = c\).
Cách giải:
+) Thay \(x = 4,\,\,y = - 1\) vào phương trình \(2x - 3y = 5\) ta được:
\(2.4 - 3.\left( { - 1} \right) = 11 \ne 5\)
\( \Rightarrow \) Cặp số \(\left( {4;\,\, - 1} \right)\) không phải là nghiệm của phương trình \(2x - 3y = 5\).
\( \Rightarrow \) Đáp án A sai.
+) Thay \(x = 1,\,\,y = - 1\) vào phương trình \(2x - 3y = 5\) ta được:
\(2.1 - 3.\left( { - 1} \right) = 5\)
\( \Rightarrow \) Cặp số \(\left( {1;\,\, - 1} \right)\) là nghiệm của phương trình \(2x - 3y = 5\).
\( \Rightarrow \) Đáp án B đúng.
+) Thay \(x = 1,\,\,y = 1\) vào phương trình \(2x - 3y = 5\) ta được:
\(2.1 - 3.1 = - 1 \ne 5\)
\( \Rightarrow \) Cặp số \(\left( {1;\,\,1} \right)\) không phải là nghiệm của phương trình \(2x - 3y = 5\).
\( \Rightarrow \) Đáp án C sai.
+) Thay \(x = - 1,\,\,y = 1\) vào phương trình \(2x - 3y = 5\) ta được:
\(2.\left( { - 1} \right) - 3.1 = - 5 \ne 5\)
\( \Rightarrow \) Cặp số \(\left( { - 1;\,\,1} \right)\) không phải là nghiệm của phương trình \(2x - 3y = 5\).
\( \Rightarrow \) Đáp án D sai.
Chọn B.
Câu 2 (TH):
Phương pháp:
Xét phương trình hoành độ giao điểm sau đó xét \(\Delta \) để xác định số nghiệm của phương trình. Từ đó suy ra số giao điểm của đồ thị hai hàm số.
Cách giải:
Xét phương trình hoành độ giao điểm của đồ thị hai hàm số \(y = {x^2}\) và \(y = 2x + 3\) ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} = 2x + 3\\ \Leftrightarrow {x^2} - 2x - 3 = 0\,\,\,\,\,\,\,\left( 1 \right)\end{array}\)
Ta có :\(\,\Delta = {b^2} - 4ac\) \( \Leftrightarrow \Delta = {\left( { - 2} \right)^2} - 4.1.\left( { - 3} \right) = 16 > 0\)
Vì \(\,\Delta > 0\) nên phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt.
Vậy số giao điểm của đồ thị hai hàm số \(y = {x^2}\) và \(y = 2x + 3\) là \(2\).
Chọn C.
Câu 3 (TH):
Phương pháp:
Nếu \(a < 0\) thì hàm số đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0\).
Cách giải:
Hàm số \(y = \left( {m - 1} \right){x^2}\) nghịch biến với \(x > 0\) khi và chỉ khi :
\(m - 1 < 0 \Leftrightarrow m < 1\).
Vậy hàm số \(y = \left( {m - 1} \right){x^2}\) nghịch biến với \(x > 0\) khi \(m < 1\).
Chọn A.
Câu 4 (NB):
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\). Xét biệt thức \(\Delta = {b^2} - 4ac\).
+) \(\Delta > 0\): Phương trình có hai nghiệm phân biệt
+) \(\Delta = 0\): Phương trình có nghiệm kép
+) \(\Delta < 0\): Phương trình vô nghiệm
Cách giải:
+) Phương trình \({x^2} - 1 = 0\) có \(a = 1,\,\,b = 0,\,\,c = - 1\)
\(\Delta = {0^2} - 4.1.\left( { - 1} \right) = 4 > 0\)
Vậy phương trình \({x^2} - 1 = 0\) có hai nghiệm phân biệt \( \Rightarrow \) Đáp án A sai.
+) Phương trình \({x^2} + 2x = 0\) có \(a = 1,\,\,b = 2,\,\,c = 0\)
\(\Delta = {2^2} - 4.1.0 = 4 > 0\)
Vậy phương trình \({x^2} + 2x = 0\) có hai nghiệm phân biệt \( \Rightarrow \) Đáp án B sai.
+) Phương trình \({x^2} - 2x + 1 = 0\) có \(a = 1,\,\,b = - 2,\,\,c = 1\)
\(\Delta = {\left( { - 2} \right)^2} - 4.1.1 = 0\)
Vậy phương trình \({x^2} - 2x + 1 = 0\) có nghiệm kép \( \Rightarrow \) Đáp án C đúng.
+) Phương trình \({x^2} - 3x + 2 = 0\) có \(a = 1,\,\,b = - 3,\,\,c = 2\)
\(\Delta = {\left( { - 3} \right)^2} - 4.1.2 = 1 > 0\)
Vậy phương trình \({x^2} - 3x + 2 = 0\) có hai nghiệm phân biệt \( \Rightarrow \) Đáp án D sai.
Chọn C.
Câu 5 (TH):
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt:
\( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta = {b^2} - 4ac > 0\end{array} \right.\).
Cách giải:
Phương trình \(m{x^2} - 2x + 1 = 0\) có hai nghiệm phân biệt khi và chỉ khi:
\(\left\{ \begin{array}{l}a \ne 0\\\Delta = {b^2} - 4ac > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\{\left( { - 2} \right)^2} - 4.m.1 > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\4 - 4m > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\4m < 4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m < 1\end{array} \right.\)
Vậy phương trình \(m{x^2} - 2x + 1 = 0\) có hai nghiệm phân biệt khi và chỉ khi \(m \ne 0\)và \(m < 1\).
Chọn B.
Câu 6 (TH):
Phương pháp:
Sử dụng góc nội tiếp.
Cách giải:
Xét \(\Delta ABC\) vuông cân tại \(A\), ta có:
\(\angle B = \angle C = {45^0}\)(tính chất)
Xét đường tròn \(\left( O \right)\), ta có:
\(\angle B = \frac{1}{2}\)sđ (góc nội tiếp bị chắn bởi cung \(AC\))
\( \Rightarrow \)sđ
Vậy số đo cung nhỏ \(AC\) bằng \({90^0}\).
Chọn D.
Câu 7 (NB):
Phương pháp:
Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
Cách giải:
Từ hình vẽ, ta thấy hai đường tròn \(\left( {{O_1}} \right)\) và \(\left( {{O_2}} \right)\) tiếp xúc ngoài có ba tiếp tuyến chung: \({A_1}{B_1},\,\,{A_2}{B_2}\), tiếp tuyến đi qua điểm \(C\).
Vậy số tiếp tuyến chung của hai đường tròn tiếp xúc ngoài là 3.
Chọn C.
Câu 8 (NB):
Phương pháp:
Sử dụng tính chất của tứ giác nội tiếp: Tứ giác có tổng hai góc đối nhau bằng \({180^0}\)
Sử dụng góc nội tiếp và góc ở tâm.
Cách giải:
Theo đề bài, ta có tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\)
\( \Rightarrow \angle BAD + \angle BCD = {180^0}\) (tính chất tứ giác nội tiếp)
\( \Leftrightarrow \angle BAD = {180^0} - \angle BCD\)
\( \Leftrightarrow \angle BAD = {180^0} - 100 = {80^0}\)
Xét đường tròn \(\left( O \right)\) có:
\(\angle BAD = \frac{1}{2}\)sđ (góc nội tiếp bị chắn bởi cung \(BD\))
\( \Rightarrow \)sđ
\( \Rightarrow \angle DOB = \)sđ (góc ở tâm)
Vậy số đo \(\angle DOB\) bằng \({160^0}\).
Chọn B.
II. TỰ LUẬN
Câu 1 (VD):
Phương pháp:
1) Lập bảng giá trị các điểm thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\) và vẽ đồ thị hàm số.
2) Dựa vào đồ thị hàm số để xác định tọa độ hai điểm \(A,\,\,B\).
Phương trình đường thẳng đi qua hai điểm \(A,\,\,B\) có dạng \(y = ax + b\).
Cách giải:
1) Trong mặt phẳng tọa độ \(Oxy\), vẽ đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Ta có bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = \frac{1}{2}{x^2}\) |
\(2\) |
\(\frac{1}{2}\) |
\(0\) |
\(\frac{1}{2}\) |
\(2\) |
\( \Rightarrow \) Đồ thị của hàm số \(y = \frac{1}{2}{x^2}\) là đường cong \(Parabol\) đi qua các điểm có tọa độ \(\left( { - 2\,;\,2} \right)\,,\)\(\,\left( { - 1\,;\,\frac{1}{2}} \right),\)\(\left( {0\,;0} \right),\,\,\)\(\left( {\frac{1}{2};\,\,1} \right),\)\(\left( {2\,;\,2} \right)\).
2) Trên đồ thị hàm số \(y = \frac{1}{2}{x^2}\) lấy điểm \(A\) có hoành độ bằng \(2\) và điểm \(B\) có tung độ bằng \(2\) (điểm \(B\) khác điểm \(A\)). Hãy viết phương trình đường thẳng \(AB\) và chứng minh \(\Delta OAB\) cân.
Theo giả thiết và dựa vào đồ thị hàm số \(y = \frac{1}{2}{x^2}\) ta có: \(A\left( {2;\,\,2} \right)\), \(B\left( { - 2;\,\,2} \right)\).
*) Viết phương trình đường thẳng \(AB\)
Giả sử phương trình đường thẳng \(AB\) có dạng \(y = ax + b\).
Vì đường thẳng \(AB\) đi qua điểm \(A\left( {2\,;\,2} \right)\) nên \(2 = 2a + b\) \(\left( 1 \right)\)
Vì đường thẳng \(AB\) đi qua điểm \(B\left( { - 2\,;\,2} \right)\) nên \(2 = - 2a + b\) \(\left( 2 \right)\)
Lấy\(\left( 1 \right)\)cộng\(\left( 2 \right)\)ta được :\(2 + 2 = \left( {2a + b} \right) + \left( { - 2a + b} \right)\)\( \Leftrightarrow 4 = 2b \Leftrightarrow b = 2\)
Với \(b = 2\), thay vào\(\left( 1 \right)\), ta có : \(2 = 2a + 2\)\( \Leftrightarrow a = 0\).
Vậy với\(a = 0\)và \(b = 2\)thì phương trình đường thẳng \(AB\) là \(y = 2\).
*) Chứng minh \(\Delta OAB\) cân
Gọi \(AB \cap Oy = \left\{ H \right\}\)
Ta có: \(AH = BH = OH = \left| 2 \right| = 2\)
Xét \(\Delta OHB\) vuông tại \(H\) có: \(O{B^2} = BH{}^2 + O{H^2}\) (định lý Py-ta-go)
Xét \(\Delta OHA\) vuông tại \(H\) có: \(O{A^2} = AH{}^2 + O{H^2}\) (định lý Py-ta-go)
Mà \(AH = BH\) nên \(OA = OB\).
\( \Rightarrow \Delta AOB\) cân tại \(O\) (định nghĩa)
Câu 2 (VD):
Phương pháp:
1) Xác định điều kiện xác định. Giải hệ phương trình để tìm \(x,\,\,y\).
2) Giải bài toán bằng cách lập phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
+) Dựa vào dữ kiện bài toán để lập phương trình.
+) Giải phương trình vừa lập sau đó đối chiếu với điều kiện đề bài và kết luận
Cách giải:
1) Giải hệ phương trình \(\left\{ \begin{array}{l}x\left( {x - 3y} \right) + y\left( {y + x} \right) = 0\\\sqrt x .\sqrt {y - 2} = 1\end{array} \right.\)
Điều kiện:
\(\left\{ \begin{array}{l}x \ge 0\\y - 2 \ge 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\y \ge 2\end{array} \right.\)
\(\left\{ \begin{array}{l}x\left( {x - 3y} \right) + y\left( {y + x} \right) = 0\\\sqrt x .\sqrt {y - 2} = 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2xy + {y^2} = 0\\x\left( {y - 2} \right) = 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\left( {x - y} \right)^2} = 0\\x\left( {y - 2} \right) = 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = y\\x\left( {y - 2} \right) = 1\,\,\,\left( * \right)\end{array} \right.\)
Thay \(x = y\) vào \(\left( * \right)\), ta có :
\(\left\{ \begin{array}{l}x = y\\y\left( {y - 2} \right) = 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = y\\{\left( {y - 1} \right)^2} - 2 = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = y\\{\left( {y - 1} \right)^2} = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = y\\\left[ \begin{array}{l}y - 1 = \sqrt 2 \\y - 1 = - \sqrt 2 \end{array} \right.\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = y\\\left[ \begin{array}{l}y = \sqrt 2 + 1\\y = - \sqrt 2 + 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = \sqrt 2 + 1\\y = \sqrt 2 + 1\end{array} \right.\\\left\{ \begin{array}{l}x = - \sqrt 2 + 1\\y = - \sqrt 2 + 1\end{array} \right.\end{array} \right.\)
Vậy hệ phương trình có hai nghiệm là:
\(\left( {x;\,\,y} \right) \in \left\{ {\left( {\sqrt 2 + 1;\,\,\sqrt 2 + 1} \right),\left( { - \sqrt 2 + 1;\,\, - \sqrt 2 + 1} \right)} \right\}.\)
2) Một hình chữ nhật có chu vi bằng \(28m\), diện tích bằng \(48{m^2}\). Tìm các kích thước của hình chữ nhật đó.
Gọi chiều rộng của hình chữ nhật là \(x\,\,\left( {m,\,\,0 < x < 7} \right)\).
Nửa chu vi của hình chữ nhật là \(28:2 = 14\,\,\left( m \right)\).
Chiều dài của hình chữ nhật là \(14 - x\,\,\left( m \right)\).
Vì chiều dài luôn lớn hơn chiều rộng \( \Rightarrow 14 - x > x\)\( \Leftrightarrow 2x < 14\)\( \Leftrightarrow x < 7\)
Vì hình chữ nhật có diện tích bằng \(48{m^2}\) nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,x\left( {14 - x} \right) = 48\\ \Leftrightarrow - {x^2} - 14x - 48 = 0\\ \Leftrightarrow {x^2} - 14x + 48 = 0\\ \Leftrightarrow {x^2} - 6x - 8x + 48 = 0\\ \Leftrightarrow \left( {x - 6} \right)\left( {x - 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 6 = 0\\x - 8 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 6\,\,\left( {tm} \right)\\x = 8\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
\( \Rightarrow \) Chiều rộng của hình chữ nhật là \(6\,\,\left( m \right)\).
\( \Rightarrow \) Chiều dài của hình chữ nhật là \(14 - 6 = 8\,\,\left( m \right)\).
Vậy chiều rộng của hình chữ nhật là \(6m\), chiều dài của hình chữ nhật là \(8m\).
Câu 3 (VD):
Phương pháp:
1) + Dựa vào tính chất của hình chữ nhật.
+ Sử dụng định lý của góc nội tiếp và định lý liên hệ giữa cung và dây.
2) Chứng minh tứ giác nội tiếp dựa vào dấu hiệu nhận biết.
Sử dụng quan hệ từ vuông góc đến song song
\(\left. \begin{array}{l}OH \bot AD\\MN\,{\rm{//}}\,AD\end{array} \right\}\)\( \Rightarrow MN \bot OH\).
3) Kẻ \(IK \bot DB\) tại \(K\).
Chứng minh \(IK = IA,\,\,IK < ID\)\( \Rightarrow IA < ID\).
Cách giải:
Cho hình chữ nhật \(ABCD\,\,\left( {AB > AD} \right)\) nội tiếp đường tròn tâm \(O\). Tia phân giác \(\angle ACD\) cắt cung nhỏ \(AD\) của đường tròn \(\left( O \right)\) tại điểm \(H\).
1) Chứng minh: Ba điểm \(A,\,\,O,\,\,C\) thẳng hàng và \(HA = HD\)
Vì hình chữ nhật \(ABCD\) nội tiếp đường tròn tâm \(O\) nên \(O\) là tâm của hình chữ nhật \(ABCD\).
Mà \(AC,\,\,BD\) là đường chéo của hình chữ nhật \(ABCD\).
\( \Rightarrow \) \(O\) là trung điểm của đường chéo \(AC\)
\( \Rightarrow \) Ba điểm \(A,\,\,O,\,\,C\) thẳng hàng.
Xét đường tròn tâm \(O\), ta có:
\(\angle ACH = \frac{1}{2}sd\,\,\,cung\,\,AH\) (\(\angle ACH\) là góc nội tiếp bị chắn bởi cung \(AH\))
\(\angle DCH = \frac{1}{2}sd\,\,\,cung\,\,DH\) (\(\angle DCH\) là góc nội tiếp bị chắn bởi cung \(DH\))
Mà \(\angle ACH = \angle DCH\) (giả thiết).
\( \Rightarrow AH = DH\) (định lý liên hệ giữa cung và dây)
Hay \(HA = HD\) (đpcm)
2) Dây \(HC\) của \(\left( O \right)\) cắt \(BD\) tại \(M\), dây \(HB\) của \(\left( O \right)\) cắt \(AC\) tại \(N\). Chứng minh: Tứ giác\(MNBC\) nội tiếp và \(MN \bot OH\).
*) Chứng minh tứ giác \(MNBC\) nội tiếp
Xét đường tròn \(\left( O \right)\), ta có:
\(\angle ACH = \frac{1}{2}sd\,\,cung\,\,AH\) (góc nội tiếp bị chắn bởi cung \(AH\))
\(\angle DBH = \frac{1}{2}\,sd\,\,DH\) (góc nội tiếp bị chắn bởi cung \(DH\))
Mà (chứng minh trên)
\( \Rightarrow \angle ACH = \angle DBH\) hay \(\angle NCM = \angle NBM\).
\( \Rightarrow \) Tứ giác \(NBCM\) nội tiếp (Dấu hiệu nhận biết :tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới hai góc bằng nhau)
*) Chứng minh \(MN \bot OH\).
\(\left. \begin{array}{l}OA = OD\,\,\left( { = R} \right)\\HA = HD\,(cmt)\end{array} \right\}\)\( \Rightarrow OH\) là đường trung trực của \(AD\)
\( \Rightarrow OH \bot AD\) \(\left( 1 \right)\)
Xét tứ giác nội tiếp \(NBCM\), ta có :
\(\angle NMB = \angle NCB\) (góc nội tiếp bị chắn bởi cung \(NB\))
Xét \(\Delta OBC\) cân tại \(O\) (vì \(OB = OC = R\)) , ta có :
\(\angle OBC = \angle OCB\) (tính chất)
Hay \(\angle NCB = \angle MBC\)
\( \Rightarrow \angle NMB = \angle MBC\,\,\left( { = \angle NCB} \right)\)
Mà \(\angle MBC\) và \(\angle NMB\) ở vị trí so le trong nên \(MN\,{\rm{//}}\,BC\) (dấu hiệu nhận biết)
\( \Rightarrow MN\,{\rm{//}}\,AD\) \(\left( {{\rm{//}}BC} \right)\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\)và\(\left( 2 \right)\) suy ra \(MN \bot OH\) (quan hệ từ vuông góc đến song song)
3) Dây \(HB\) của \(\left( O \right)\) cắt \(AD\) tại \(I\). Chứng minh \(IA < ID\) và \(AB.AC = BH.BI\).
*) Chứng minh \(IA < ID\)
Kẻ \(IK \bot DB\) tại \(K\).
Xét \(\Delta ABI\) và \(\Delta KBI\) ta có:
\(\angle IAB = \angle IKB\,\,\left( { = {{90}^0}} \right)\)
\(IB\) là cạnh chung
\(\angle ABI = \angle KBI\) (góc nội tiếp bị chắn bởi hai cung bằng nhau \(HA\) và \(HD\))
\( \Rightarrow \Delta ABI = \Delta KBI\) (cạnh huyền – góc nhọn)
\( \Rightarrow IA = IK\) (hai cạnh tương ứng)
Mà \(IK < ID\) (quan hệ giữa đường vuông góc và đường xiên trong \(\Delta IKD\) vuông tại \(D\))
\( \Rightarrow IA < ID\) (đpcm)
*) Chứng minh \(AB.AC = BH.BI\)
Xét đường tròn \(\left( O \right)\) có ta có:
\(\angle AHC = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow BH = CH\) (liên hệ giữa cung và dây)
Xét \(\Delta AIB\) và \(\Delta HAC\) ta có:
\(\angle IAB = \angle AHC\,\,\left( { = {{90}^0}} \right)\)
\(\angle IBA = \angle ACH\) (góc nội tiếp cùng chắn bởi cung \(AH\))
\( \Rightarrow \Delta AIB \sim \Delta HAC\) (góc - góc)
\( \Rightarrow \frac{{AB}}{{CH}} = \frac{{BI}}{{AC}}\) (tỷ lệ cặp cạnh tương ứng)
\( \Rightarrow AB.AC = CH.BI\)
Mà \(BH = CH\)(chứng minh trên)
\( \Rightarrow AB.AC = BH.BI\) (đpcm)
Câu 4 (VDC):
Phương pháp:
Phương trình \(\left( 1 \right)\) có đúng hai nghiệm phân biệt khi phương trình \({x^2} + 5mx + 4{m^2}\) có nghiệm duy nhất khác \(1\).
Cách giải:
Cho phương trình: \(\left( {x - 1} \right)\left( {{x^2} + 5mx + 4{m^2}} \right) = 0\,\,\,\,\,\left( 1 \right)\) (với \(m\) là tham số)
Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có đúng hai nghiệm phân biệt.
Xét phương trình \(\left( 1 \right)\):
\(\begin{array}{l}\left( {x - 1} \right)\left( {{x^2} + 5mx + 4{m^2}} \right) = 0\,\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\{x^2} + 5mx + 4{m^2} = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} + 5mx + 4{m^2} = 0\,\,\,\left( 2 \right)\end{array} \right.\end{array}\)
Để phương trình \(\left( 1 \right)\) có đúng hai nghiệm phân biệt thì phương trình \(\left( 2 \right)\) phải có nghiệm duy nhất và nghiệm đó khác 1.
Phương trình \(\left( 2 \right)\) có nghiệm duy nhất khi và chỉ khi :
\(\begin{array}{l}\,\,\,\,\,\,\,\Delta = {b^2} - 4ac = 0\\ \Leftrightarrow {\left( {5m} \right)^2} - 4.1.4{m^2} = 0\\ \Leftrightarrow 9{m^2} = 0\\ \Leftrightarrow m = 0\end{array}\).
Với \(m = 0\) phương trình \(\left( 2 \right)\) trở thành: \({x^2} = 0 \Leftrightarrow x = \,0\,\,\left( {x \ne 1} \right)\)
\( \Rightarrow m = 0\) (thỏa mãn)
Vậy \(m = 0\) thì phương trình \(\left( {x - 1} \right)\left( {{x^2} + 5mx + 4{m^2}} \right) = 0\) có đúng 2 nghiệm phân biệt.