Đề bài
I. TRẮC NGHIỆM (1 điểm) Chọn chữ cái đúng trước câu trả lời đúng.
Câu 1: Cặp số \(\left( { - 1;2} \right)\) là nghiệm của hệ phương trình nào sau đây?
A. \(\left\{ \begin{array}{l}x + 5y = 9\\6x + 2y = - 2\end{array} \right.\) B. \(\left\{ \begin{array}{l} - 2x + y = 7\\x - \dfrac{3}{4}y = 3\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x + y = 1\\ - 2x + y = 4\end{array} \right.\) D. \(\left\{ \begin{array}{l}2x - 2y = 0\\x + y = 3\end{array} \right.\)
Câu 2: Điều kiện của m để phương trình \({x^2} - 2mx + {m^2} - 4 = 0\) có hai nghiệm \({x_1} = 0,\,\,{x_2} > 0\) là:
A. \(m = - 2\) B. \(m = 2\)
C. \(m = \pm 2\) D. \(m = 16\)
Câu 3: Cho đường tròn \(\left( {O;R} \right)\) đường kính AB, dây\(AC = R\). Khi đó số đo độ của cung nhỏ BC là:
A. \({60^o}\) B. \({120^o}\)
C. \({90^o}\) D. \({150^o}\)
Câu 4: Độ dài của một đường tròn là \(10\pi \) (cm). Diện tích của hình tròn đó là:
A. \(10\pi \;\left( {c{m^2}} \right)\) B. \(100\pi \;\left( {c{m^2}} \right)\)
C. \(50\pi \;\left( {c{m^2}} \right)\) D. \(25\pi \;\left( {c{m^2}} \right)\)
II. TỰ LUẬN (9 điểm)
Câu 1 (2,5 điểm):
1) Giải hệ phương trình sau: \(\left\{ \begin{array}{l}\dfrac{2}{{x - 2}} + \dfrac{1}{{y + 1}} = 3\\\dfrac{3}{{x - 2}} - \dfrac{2}{{y + 1}} = 8\end{array} \right.\)
2) Trong mặt phẳng tọa độ Oxy cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 2mx - 2m + 1\)
a) Với\(m = - 1\), hãy tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\).
b) Tìm m để \(\left( P \right)\) và \(\left( d \right)\) cắt nhau tại 2 điểm phân biệt \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) sao cho tổng các tung độ của hai giao điểm bằng 2.
Câu 2 (2,5 điểm): Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một đội xe theo kế hoạch chở hết 120 tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó chở vượt mức 5 tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 5 tấn. Hỏi theo kế hoạch đội xe chở hết số hàng đó trong bao nhiêu ngày?
Câu 3 (3,5 điểm): Cho đường tròn \(\left( O \right)\) có dây cung CD cố định. Gọi M là điểm nằm chính giữa cung nhỏ CD. Đường kính MN của đường tròn \(\left( O \right)\) cắt dây CD tại I. Lấy điểm E bất kỳ trên cung lớn CD (E khác C,D,N); ME cắt CD tại K. Các đường thẳng NE và CD cắt nhau tại P.
a) Chứng minh rằng: Tứ giác IKEN nội tiếp.
b) Chứng minh: \(EI.MN = NK.ME\).
c) NK cắt MP tại Q. Chứng minh: IK là phân giác của \(\angle EIQ\).
d) Từ C vẽ đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung lớn CD (E khác C, D, N) thì H luôn chạy trên một đường cố định.
Câu 4 (0,5 điểm): Cho \(a,\;b,\;c > 0\), chứng minh rằng:
\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\)\( < \sqrt {\dfrac{a}{{b + c}}} + \sqrt {\dfrac{b}{{c + a}}} + \sqrt {\dfrac{c}{{a + b}}} \)
Đ/a TN
|
1A |
2B |
3B |
4D |
Câu 1:
Phương pháp:
Thay \(\left( {x;y} \right) = \left( { - 1;2} \right)\) vào từng hệ phương trình để kiểm tra, nếu thỏa mãn thì là nghiệm và ngược lại.
Cách giải:
\(\left\{ \begin{array}{l} - 1 + 5.2 = 9\\6\left( { - 1} \right) + 2.2 = - 2\end{array} \right.\)
Vậy \(\left( { - 1;2} \right)\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 5y = 9\\6x + 2y = - 2\end{array} \right.\)
Chọn A
Câu 2:
Phương pháp:
Từ dữ kiện đề bài sử dụng công thức nghiệm thu gọn kết hợp định lý Vi-ét để tìm m
Cách giải:
\({x^2} - 2mx + {m^2} - 4 = 0\)
\(\Delta ' = {m^2} - {m^2} + 4 = 4 > 0\) với mọi \(m \Rightarrow \) phương trình có hai nghiệm phân biệt với mọi \(m.\)
Ta có \({x_1} = 0,\,\,{x_2} > 0\) và theo định lý Vi-ét ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{x_1} + {x_2} = 2m > 0\\{x_1}{x_2} = {m^2} - 4 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\{m^2} = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\left[ \begin{array}{l}m = 2\\m = - 2\end{array} \right.\end{array} \right. \Leftrightarrow m = 2\end{array}\)
Vậy với \(m = 2\) thỏa mãn yêu cầu đề bài.
Chọn B
Câu 3:
Phương pháp:
Sử dụng tính chất, dấu hiệu nhận biết tam giác đều để tính \(\angle BOC\) từ đó suy ra số đo cung nhỏ BC
Cách giải:
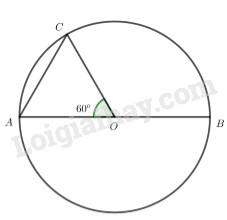
Cho đường tròn \(\left( {O;R} \right)\) đường kính AB \( \Rightarrow OA = OB = R\)
Mặt khác dây\(AC = R\)\( \Rightarrow OA = OC = AC = R\)
\( \Rightarrow \Delta OAC\) đều \( \Rightarrow \angle AOC = {60^o}\)
\( \Rightarrow \angle BOC = {180^o} - \angle AOC\)\( = {120^o}\) (hai góc kề bù)
\( \Rightarrow \) sđ (số đo góc ở tâm bằng số đo cung bị chắn)
Chọn B
Câu 4:
Phương pháp:
Từ công thức tính chu vi hình tròn rút ra R, từ đó tính diện tích hình tròn đó.
Cách giải:
Độ dài của một đường tròn chính là chu vi hình tròn \( \Rightarrow 2\pi .R = 10\pi \Rightarrow R = 5\;\;\left( {cm} \right)\)
Diện tích hình tròn đó là: \(\pi {R^2} = 25\pi \;\;\left( {c{m^2}} \right).\)
Chọn D
LG câu 1
Phương pháp giải:
1) Đặt điều kiện cho hệ phương trình sau đó giải hệ phương trình bằng cách đặt ẩn phụ.
2) a) Thay \(m = - 1\) vào phương trình đường thẳng d.
+) Lập phương trình hoành độ giao điểm, giải phương trình đó để tìm hoành độ 2 giao điểm, từ đó suy ra tọa độ của chúng.
b) \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt A và B \( \Leftrightarrow \) phương trình hoành độ giao điểm có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)
Từ đề bài tìm ra hệ thức liên hệ giữa \({x_1}\) và \({x_2}\), biến đổi biểu thức đó sao cho chỉ còn \({x_1} + {x_2}\) và \({x_1}.{x_2}\), sử dụng hệ thức Vi-ét thế vào để tìm m.
Lời giải chi tiết:
1) Giải hệ phương trình sau: \(\left\{ \begin{array}{l}\dfrac{2}{{x - 2}} + \dfrac{1}{{y + 1}} = 3\\\dfrac{3}{{x - 2}} - \dfrac{2}{{y + 1}} = 8\end{array} \right.\)
Điều kiện: \(\left\{ \begin{array}{l}x - 2 \ne 0\\y + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\y \ne - 1\end{array} \right.\)
Đặt: \(\left\{ \begin{array}{l}\dfrac{1}{{x - 2}} = a\\\dfrac{1}{{y + 1}} = b\end{array} \right.\;\;\left( {a,\;b \ne 0} \right),\) khi đó hệ phương trình trở thành:
\(\begin{array}{l}\left\{ \begin{array}{l}2a + b = 3\\3a - 2b = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b = 6\\3a - 2b = 8\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2a + b = 3\\7a = 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 1\end{array} \right.\;\;\left( {tm} \right)\\ \Rightarrow \left\{ \begin{array}{l}\dfrac{1}{{x - 2}} = 2\\\dfrac{1}{{y + 1}} = - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 = \dfrac{1}{2}\\y + 1 = - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{5}{2}\;\;\left( {tm} \right)\\y = - 2\;\;\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {\dfrac{5}{2}; - 2} \right)\).
2) Trong mặt phẳng tọa độ Oxy cho Parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = 2mx - 2m + 1\)
a) Với \(m = - 1\), hãy tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\).
Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) là :
\(2mx - 2m + 1 = {x^2}\) \( \Leftrightarrow {x^2} - 2mx + 2m - 1 = 0\;\;\;\left( 1 \right)\)
Với \(m = - 1,\;\;\left( 1 \right)\) trở thành \({x^2} + 2x - 3 = 0\)
Có \(\Delta ' = {1^2} + 3 = 4 \Rightarrow \sqrt {\Delta '} = 2\)
Với \(m = - 1\) phương trình có hai nghiệm \(\left[ \begin{array}{l}x = - 1 + 2 = 1 \Rightarrow y = 1\\x = - 1 - 2 = - 3 \Rightarrow y = 9\end{array} \right..\)
Vậy với \(m = - 1\) giao điểm của \(\left( P \right)\) và \(\left( d \right)\)là hai điểm có tọa độ \(\left( {1;1} \right)\) và \(\left( { - 3;9} \right)\)
b) Tìm m để \(\left( P \right)\) và \(\left( d \right)\) cắt nhau tại 2 điểm phân biệt \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) sao cho tổng các tung độ của hai giao điểm bằng 2.
Để \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt A và B \( \Leftrightarrow \) (1) có hai nghiệm phân biệt
\( \Leftrightarrow \Delta ' = {m^2} - \left( {2m - 1} \right)\) \( = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2} > 0\)\( \Leftrightarrow m - 1 \ne 0 \Leftrightarrow m \ne 1\)
Gọi \({x_1},{x_2}\) lần lượt là hoành độ của hai điểm A và B
\( \Rightarrow {x_1},{x_2}\) là 2 nghiệm của (1)
Theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = 2m - 1\end{array} \right.\)
Vì \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) đều thuộc \(\left( P \right):y = {x^2}\) \( \Rightarrow \left\{ \begin{array}{l}{y_1} = {x_1}^2\\{y_2} = {x_2}^2\end{array} \right.\)
Tổng các tung độ của hai giao điểm bằng 2
\(\begin{array}{l} \Rightarrow {y_1} + {y_2} = 2\\ \Leftrightarrow {x_1}^2 + {x_2}^2 = 2\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} = 2\\ \Leftrightarrow {\left( {2m} \right)^2} - 2\left( {2m - 1} \right) = 2\\ \Leftrightarrow 4{m^2} - 4m + 2 = 2\\ \Leftrightarrow 4{m^2} - 4m = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,\,\left( {tm} \right)\\m = 1\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy với \(m = 0\) thỏa mãn yêu cầu đề bài.
LG câu 2
Phương pháp giải:
+ Phân tích kỹ đề bài.
+ Gọi thời gian chở hàng theo kế hoạch là x (ngày), đã biết tổng số hàng theo kế hoạch và thực tế \( \Rightarrow \) lập phương trình theo năng suất để tìm x.
Lời giải chi tiết:
Gọi thời gian đội đó chở hàng theo kế hoạch là x (ngày) \(\left( {x > 1} \right).\)
Năng suất của đội đó theo kế hoạch là \(\dfrac{{120}}{x}\) (tấn/ngày)
Thời gian chở đội đó hàng thực tế là \(x - 1\) (ngày)
Năng suất thực tế đội đó chở hàng là \(\dfrac{{125}}{{x - 1}}\) (tấn/ngày)
Vì đội xe chở hàng vượt mức 5 tấn/ngày nên ta có phương trình
\(\begin{array}{l}\dfrac{{125}}{{x - 1}} - \dfrac{{120}}{x} = 5\\ \Leftrightarrow 125x - 120\left( {x - 1} \right) = 5x\left( {x - 1} \right)\\ \Leftrightarrow 5x + 120 = 5{x^2} - 5x\\ \Leftrightarrow 5{x^2} - 10x - 120 = 0\\ \Leftrightarrow \left( {x - 6} \right)\left( {x + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 6\,\,\,\left( {tm} \right)\\x = - 4\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy thời gian chở hàng theo kế hoạch là 6 ngày.
LG câu 3
Phương pháp giải:
+) Chứng minh IKEN là tứ giác có tổng hai góc đối bằng \({180^o}\)
+) Chứng minh (g.g) để suy ra đpcm
+) Chứng minh tứ giác NIQP nội tiếp kết hợp a) để suy ra \(\angle QIP = \angle EIK\) từ đó ta được đpcm
Lời giải chi tiết:
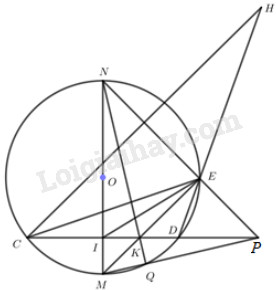
a) Chứng minh rằng: Tứ giác IKEN nội tiếp.
Xét đường tròn \(\left( O \right)\)đường kính MN có M là điểm chính giữa cung nhỏ CD
\( \Rightarrow MN \bot CD\) tại I \( \Rightarrow \angle NID = {90^o}\)
\(E \in \left( O \right) \Rightarrow \angle MEN = {90^o}\) (góc nội tiếp chắn nửa đường tròn)
Xét tứ giác IKEN có: \(\angle NID + \angle MEN\) \( = {90^o} + {90^o} = {180^o}\)
Mà 2 góc này ở vị trí đối nhau nên tứ giác IKEN nội tiếp. (dhnb)
b) Chứng minh: \(EI.MN = NK.ME\).
Tứ giác IKEN nội tiếp (cmt) nên \(\angle MEI = \angle MNK\) (góc nội tiếp cùng chắn cung IK )
Xét \(\Delta MEI\) và \(\Delta MNK\) có:
\(\begin{array}{l}\angle E\;\;chung\\\angle MEI = \angle MNK\;\;\;\left( {cmt} \right)\\ \Rightarrow \Delta MEI \backsim \Delta MNK\;\;\left( {g - g} \right)\\ \Rightarrow \dfrac{{EI}}{{NK}} = \dfrac{{ME}}{{MN}}\end{array}\)
\( \Rightarrow EI.MN = NK.ME\) (đpcm)
c) NK cắt MP tại Q. Chứng minh: IK là phân giác của \(\angle EIQ\).
Xét \(\Delta MNP\) có: \(ME \bot NP\,\;\;\left( {cmt} \right)\,;\,\)\(PI \bot MN\;\;\left( {cmt} \right)\,;\) \(ME \cap PI = \left\{ K \right\}\)
\( \Rightarrow K\) là trực tâm \(\Delta MNP \Rightarrow NK \bot MP\) tại \(Q \Rightarrow \angle NQP = {90^o}\)
Xét tứ giác NIQP có \(\angle NIP = \angle NQP = {90^o}\) mà 2 góc này cùng nhìn đoạn NP
\( \Rightarrow \) Tứ giác NIQP nội tiếp (dhnb) \( \Rightarrow \angle QNP = \angle QIP\) (hai góc nội tiếp cùng chắn cung PQ) (1)
Tứ giác IKEN nội tiếp (cm a) \( \Rightarrow \angle QNP = \angle EIK\) (cùng chắn EK) (2)
Từ (1) và (2) \( \Rightarrow \angle QIP = \angle EIK\)\( \Rightarrow \) IK là phân giác của \(\angle EIQ\;\;\;\left( {dpcm} \right).\)
d) Từ C vẽ đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung lớn CD (E khác C, D, N) thì H luôn chạy trên một đường cố định.
Ta có: \(ME \bot NP\;\left( {cmt} \right);\,\,\) \(CH \bot NP\;\;\left( {gt} \right)\)\( \Rightarrow ME//CH\)(từ vuông góc đến song song)
\( \Rightarrow \angle DEM = \angle DHC\) (đồng vị) ;
\(\angle MEC = \angle ECH\) (so le trong)
Mà \(\angle DEM = \angle MEC\) (2 góc nội tiếp chắn 2 cung bằng nhau)
\( \Rightarrow \angle EHC = \angle ECH\;\;\) \(\left( { = \angle DEM = \angle MEC} \right)\)
\( \Rightarrow \Delta EHC\) cân tại E Þ EN là trung trực của CH (tính chất)
Mặt khác dễ dàng chứng minh IN là trung trực của CD \(\left( {IN \bot CD,\;\;IC = ID} \right).\)
\( \Rightarrow \) N là tâm đường tròn ngoại tiếp \(\Delta DCH\) \( \Rightarrow H \in \left( {N;NC} \right)\)
Mà N, C, D cố định \( \Rightarrow \) H thuộc đường tròn tâm N cố định bán kính NC không đổi (đpcm)
LG câu 4
Phương pháp giải:
Chứng minh \(\sqrt {\dfrac{a}{{b + c}}} \ge \dfrac{{2a}}{{a + b + c}}\) và \(\dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}\), từ đó suy ra đpcm.
Lời giải chi tiết:
Cho \(a,b,c > 0\), chứng minh rằng: \(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\)\( < \sqrt {\dfrac{a}{{b + c}}} + \sqrt {\dfrac{b}{{c + a}}} + \sqrt {\dfrac{c}{{a + b}}} \)
Áp dụng bất đẳng thức Cô-si cho hai số dương a và \(b + c\) ta được:
\(\dfrac{{a + \left( {b + c} \right)}}{2} \ge \sqrt {a\left( {b + c} \right)} > 0\) \( \Rightarrow \dfrac{2}{{a + b + c}} \le \dfrac{1}{{\sqrt {a\left( {b + c} \right)} }}\)
\( \Rightarrow \dfrac{{2a}}{{a + b + c}} \le \dfrac{a}{{\sqrt {a\left( {b + c} \right)} }}\) \( \Leftrightarrow \sqrt {\dfrac{a}{{b + c}}} \ge \dfrac{{2a}}{{a + b + c}}\;\;\;\left( 1 \right)\)
Chứng minh tương tự ta được: \(\left\{ \begin{array}{l}\sqrt {\dfrac{b}{{c + a}}} \ge \dfrac{{2b}}{{a + b + c}}\;\;\;\left( 2 \right)\\\sqrt {\dfrac{c}{{a + b}}} \ge \dfrac{{2c}}{{a + b + c}}\;\;\;\left( 3 \right)\end{array} \right.\)
Cộng (1), (2) và (3) vế theo vế ta được: \(\sqrt {\dfrac{a}{{b + c}}} + \sqrt {\dfrac{b}{{c + a}}} + \sqrt {\dfrac{c}{{a + b}}} \ge 2\) (*)
Ta chứng minh \(\dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}\;\;\;\left( 4 \right)\)
Thật vậy ta có \(\dfrac{a}{{a + b}} < \dfrac{{a + c}}{{a + b + c}}\) \( \Leftrightarrow {a^2} + ab + ac < {a^2} + ab + ac + bc\)
\( \Leftrightarrow bc > 0\) (luôn đúng do \(a,b,c > 0\))
Tương tự ta có \(\left\{ \begin{array}{l}\dfrac{b}{{b + c}} < \dfrac{{b + a}}{{a + b + c}}\;\;\;\left( 5 \right)\\\dfrac{c}{{c + a}} < \dfrac{{c + b}}{{a + b + c}}\;\;\;\left( 6 \right)\end{array} \right.\)
Cộng (4), (5) và (6) vế theo vế ta được: \(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < 2\) (**)
Từ (*) và (**) suy ra \(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\) \( < \sqrt {\dfrac{a}{{b + c}}} + \sqrt {\dfrac{b}{{c + a}}} + \sqrt {\dfrac{c}{{a + b}}} \) (đpcm)
Nguồn sưu tầm
soanvan.me
