Đề bài
Câu 1: Giải các phương trình sau:
a) \(3x(x - 2) = 11 - 2{x^2}.\)
b) \({(x + 1)^2} - 2x + 1 = {x^4}.\)
Câu 2: Một mảnh đất hình chữ nhật có chu vi 80m, biết ba lần chiều rộng kém 2 lần chiều dài là 5m. Tính diện tích mảnh đất.
Câu 3: Cho hàm số: \(y = - \dfrac{{{x^2}}}{4}\,\,(P);y = \dfrac{x}{2} - 2\,\,\,(d).\)
a) Vẽ đồ thị d và P.
b) Tính tọa độ giao điểm d và P.
Câu 4: Cho phương trình: \({x^2} - 2mx - 4m - 5 = 0.\)
a) Chứng tỏ phương trình trên luôn có 2 nghiệm phân biệt với mọi m.
b) Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn: \(x_1^2 + x_2^2 - {x_1}{x_2} = 2{x_1} + 2{x_2} + 27.\)
Câu 5: Một trường tổ chức cho 250 người bao gồm giáo viên và học sinh đi tham quan Suối Tiên. Biết giá vé vào cổng giáo viên là 80.000 đồng, học sinh là 60.000 đồng, đi vào đúng dịp giỗ tổ Hùng Vương nên giảm 5% vé vào, vì vậy nhà trường phải trả tổng cộng 14.535.000 đồng. Hỏi có bao nhiêu giáo viên và học sinh đi tham quan?
Câu 6: Đường tròn đi qua 2 đỉnh và tiếp xúc cạnh 1 hình vuông. Tính bán kính R của đường tròn biết cạnh hình vuông là 12 cm.
Câu 7: Từ A ngoài (O), vẽ tiếp tuyến AB, AC, H là giao OA và BC.
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông BC.
b) Qua C vẽ d // OA, qua O vẽ đường vuông góc OB cắt (O) và d tại F và K (O nằm giữa F và K), AF cắt (O) tại E. Chứng minh rằng: \(A{B^2} = AE.FA;\)\(BE.FC = BF.EC\)
c) Chứng minh OCKA là hình thang cân.
LG câu 1
Phương pháp giải:
Đây là các phương trình bậc 2 và trùng phương, ta đưa về phương trình tích.
Lời giải chi tiết:
\(\begin{array}{l}a)\,\,3x(x - 2) = 11 - 2{x^2}.\\ \Leftrightarrow 3{x^2} - 6x + 2{x^2} - 11 = 0\\ \Leftrightarrow 5{x^2} - 6x - 11 = 0\\ \Leftrightarrow (x + 1)(5x - 11) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\5x - 11 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \dfrac{{11}}{5}\end{array} \right..\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 1;\,\dfrac{{11}}{5}} \right\}.\)
\(\begin{array}{l}b)\,\,\,{(x + 1)^2} - 2x + 1 = {x^4}\\ \Leftrightarrow {x^2} + 2x + 1 - 2x + 1 = {x^4}\\ \Leftrightarrow {x^4} - {x^2} - 2 = 0\,\,\,\,\left( * \right)\end{array}\)
Đặt \({x^2} = t\,\,\left( {t \ge 0} \right)\), phương trình (*) trở thành:
\(\begin{array}{l}{t^2} - t - 2 = 0\\ \Leftrightarrow \left( {t + 1} \right)\left( {t - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t + 1 = 0\\t - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = - 1\,\,\,\left( {ktm} \right)\\t = 2\,\,\,\left( {tm} \right)\end{array} \right.\\ \Rightarrow {x^2} = 2\\ \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right..\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ { - \sqrt 2 ;\,\,\sqrt 2 } \right\}.\)
LG câu 2
Phương pháp giải:
Giải bài toán bằng cách lập phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
+) Dựa vào dữ kiện bài toán để lập phương trình.
+) Giải phương trình vừa lập sau đó đối chiếu với điều kiện đề bài và kết luận.
Lời giải chi tiết:
Gọi chiều rộng mảnh đất là \(x\,\,\left( m \right),\,\,\,\left( {x > 0} \right).\)
Nửa chu vi của mảnh đất là: \(80:2 = 40\,\,\left( m \right).\)
\( \Rightarrow \) Chiều dài của mảnh đất là:\(40 - x\,\,\left( m \right)\)
Do 3 lần chiều rộng kém 2 lần chiều dài là 5m nên ta có phương trình:
\(\begin{array}{l}3x = 2\left( {40 - x} \right) - 5\\ \Leftrightarrow 3x = 80 - 2x - 5\\ \Leftrightarrow 5x = 75\\ \Leftrightarrow x = 15\,\,\,\left( {tm} \right)\end{array}\)
Chiều dài mảnh đất là : \(40 - 15 = 25\,\,\,(m).\)
Diện tích mảnh đất là : 15.25 = \(15.25 = 375\,\,\,\left( {{m^2}} \right).\)
LG câu 3
Phương pháp giải:
1) Lập bảng giá trị các điểm thuộc đồ thị hàm số (P) và vẽ đồ thị hàm số.
2) Lập phương trình hoành độ giao điểm của (d) cắt (P).
+) Để (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm phải có hai nghiệm phân biệt tức là \(\Delta > 0.\)
Lời giải chi tiết:
Cho hàm số: \(y = - \dfrac{{{x^2}}}{4}(P);y = \dfrac{x}{2} - 2\,\,\,(d).\)
a) Vẽ đồ thị d và P.
+) Vẽ đồ thị hàm số : \(\left( P \right):\,\,y = - \dfrac{{{x^2}}}{4}\)
Ta có bảng giá trị:
|
\(x\) |
\( - 4\) |
\( - 2\) |
0 |
2 |
4 |
|
\(\;y = - \dfrac{{{x^2}}}{4}\) |
\( - 4\) |
\( - 1\) |
0 |
\( - 1\) |
\( - 4\) |
Vậy đồ thị hàm số \(\left( P \right):\,\,\,y = - \dfrac{{{x^2}}}{4}\) là đường cong đi qua các điểm \(\left( { - 4; - 4} \right),\,\,\left( { - 2; - 1} \right),\,\)\(\left( {0;\,0} \right),\,\,\left( {2; - 1} \right),\,\,\left( {4; - 4} \right).\) +) Vẽ đồ thị hàm số \(\left( d \right):\,\,y = \dfrac{x}{2} - 2:\)
Ta có bảng giá trị:
|
\(x\) |
0 |
\(4\) |
|
\(y = \dfrac{x}{2} - 2\) |
\( - 2\) |
0 |
Vậy đồ thị hàm số \(\left( d \right):\,\,y = \dfrac{x}{2} - 2\) là đường thẳng đi qua các điểm \(\left( {0; - 2} \right),\,\,\left( {4;\,0} \right).\)
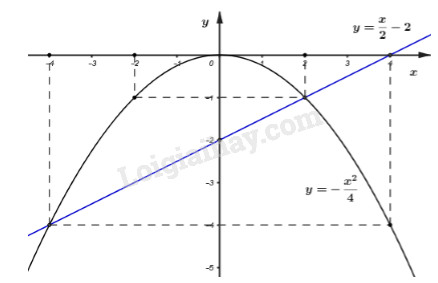
b) Tính tọa độ giao điểm (D) và (P).
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
\(\begin{array}{l}\dfrac{{ - {x^2}}}{4} = \dfrac{x}{2} - 2\\ \Leftrightarrow {x^2} + 2x - 8 = 0\\ \Leftrightarrow (x - 2)(x + 4) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = - 1\\x = - 4 \Rightarrow y = - 4\end{array} \right..\end{array}\)
Vậy tọa độ giao điểm là: \(\left( {2; - 1} \right),\,\,\left( { - 4;\, - 4} \right).\)
LG câu 4
Phương pháp giải:
Bước 1: Tìm m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) : Phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2} \Leftrightarrow \Delta \,\,\left( {\Delta '} \right) > 0.\)
Bước 2: Phân tích biểu thức A về dạng chứa các hệ thức Viet sau đó áp dụng hệ thức Vi-et vào tìm được m và đối chiếu với điều kiện sau đó kết luận.
Hệ thức Viet như sau: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)
Lời giải chi tiết:
Cho phương trình: \({x^2} - 2mx - 4m - 5 = 0.\)
a) Chứng tỏ phương trình trên luôn có 2 nghiệm phân biệt với mọi m.
Ta có \(\Delta ' = {m^2} + 4m + 5\)\( = {(m + 2)^2} + 1 > 0\) với mọi m
Do đó phương trình trên luôn có 2 nghiệm phân biệt với mọi \(m.\)
b) Tìm m để phương trình có 2 nghiệm phân biệt thỏa mãn: \(x_1^2 + x_2^2 - {x_1}{x_2} = 2{x_1} + 2{x_2} + 27.\)
Áp dụng định lý Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = - 4m - 5\end{array} \right.\)
Theo đề bài ta có :
\(\begin{array}{l}x_1^2 + x_2^2 - {x_1}{x_2} = 2{x_1} + 2{x_2} + 27.\\ \Leftrightarrow {({x_1} + {x_2})^2} - 3{x_1}{x_2} - 2({x_1} + {x_2}) - 27 = 0\\ \Leftrightarrow 4{m^2} + 3(4m + 5) - 4m - 27 = 0\\ \Leftrightarrow 4{m^2} + 8m - 12 = 0\\ \Leftrightarrow {m^2} + 2m - 3 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 3\end{array} \right..\end{array}\)
Vậy \(m = 1,\,\,m = - 3\) thỏa mãn yêu cầu bài toán.
LG câu 5
Phương pháp giải:
Giải bài toán bằng cách lập hệ phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chưa biết theo ẩn vừa gọi và các đại lượng đã biết.
+) Dựa vào dữ kiện bài toán để lập hệ phương trình.
+) Giải hệ phương trình vừa lập sau đó đối chiếu với điều kiện đề bài và kết luận.
Lời giải chi tiết:
Gọi số giáo viên là \(a,\) số học sinh là \(b\) (người), \(\left( {a,\,b \in N*,\,\,a,\,b < 250} \right).\)
Tổng số giáo viên và học sinh đi tham quan là 250 người nên ta có phương trình: \(a + b = 250\,\,\,\left( 1 \right)\)
Giá tiền vé vào cổng của mỗi giáo viên sau khi giảm giá là: \(80.0000 \times 95:100 = 76.000\) (đồng)
Giá tiền vé vào cổng của mỗi học sinh sau khi giảm giá là: \(60.000 \times 95:100 = 57.000\) (đồng)
Tổng số tiền nhà trường phải trả là 14.535.000 đồng nên ta có phương trình:
\(76.000a + 57.000b = 14.535.000\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}a + b = 250\\76.000a + 57.000b = 14.535.000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}76.000a + 76.000b = 19.000.000\\76.000a + 57.000b = 14.535.000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 15\,\,\left( {tm} \right)\\b = 235\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy: có 15 giáo viên và 235 học sinh đi tham quan.
LG câu 6
Phương pháp giải:
Áp dụng định lý Pytago, lưu ý điểm tiếp xúc E sẽ là trung điểm CD.
Lời giải chi tiết:
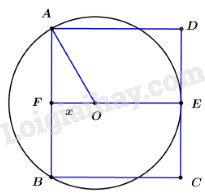
Giả sử hình tròn đi qua hai đỉnh A, B và tiếp xúc với cạnh CD của hình vuông ABCD.
Ta có hình vẽ:
Gọi \(E\) là điểm tiếp xúc của \(\left( O \right)\) và \(CD.\)
Kéo dài \(EO\) cắt \(AB\) tại \(F \Rightarrow F\) là trung điểm của \(AB.\)
Gọi \(OF = x\,\,\left( {0 < x < 12} \right).\)
Ta có: \(AF = \dfrac{1}{2}AB = 6\,cm.\)
Áp dụng định lý Pi-ta-go cho \(\Delta AOF\) vuông tại \(F\) ta có:
\(\begin{array}{l}O{F^2} = O{A^2} - A{F^2}\\ \Leftrightarrow {x^2} = {R^2} - {6^2}\\ \Leftrightarrow {x^2} = {R^2} - 36\,\,\,\left( * \right)\end{array}\)
Lại có:
\(\begin{array}{l}EF = 12 = OF + OE\\ \Leftrightarrow x + R = 12\\ \Leftrightarrow x = 12 - R.\end{array}\)
Thay \(x = 12 - R\) vào (*) ta được:
\(\begin{array}{l}{\left( {12 - R} \right)^2} = {R^2} - 36\\ \Leftrightarrow 144 - 24R + {R^2} = {R^2} - 36\\ \Leftrightarrow 24R = 180\\ \Leftrightarrow R = \dfrac{{15}}{2} = 7,5\,cm.\end{array}\)
Vậy bán kính đường tròn thỏa mãn yêu cầu bài toán là: \(R = 7,5\,\,cm.\)
LG câu 7
Phương pháp giải:
a) Chứng minh đây là tứ giác có 2 góc đối diện vuông.
b) Sử dụng 2 cặp tam giác đồng dạng và AB = AC để suy ra hệ thức.
c) Sử dụng tính chất hình thang nội tiếp đường tròn là hình thang cân.
Lời giải chi tiết:
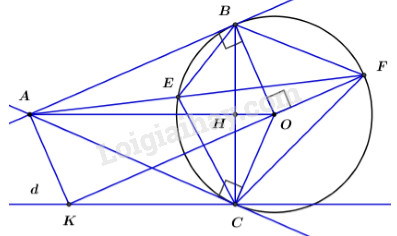
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông BC.
Do AB, AC là tiếp tuyến từ A đến (O) nên: \(\angle ABO = \angle ACO = {90^0}\)
Xét tứ giác \(OBAC\) ta có:
\(\angle ABO + \angle ACO\) \( = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow OBAC\) là tứ giác nội tiếp (dhnb).
Ta có: \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \Delta ABC\) cân tại \(A.\) (định nghĩa)
Lại có: \(AO\) là phân giác của \(\angle BAC\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow AO\) vừa là đường cao, vừa là đường phân giác của \(\Delta ABC \Rightarrow AO \bot BC = \left\{ H \right\}\) (đpcm)
b) Qua C vẽ d // OA, qua O vẽ đường vuông góc OB cắt (O) và d tại F và K (O nằm giữa F và K), AF cắt (O) tại E. Chứng minh rằng: \(A{B^2} = AE.FA;\)\(BE.FC = BF.EC\)
Ta có: \(\angle ABE = \angle BFA\,\)(\( = \dfrac{1}{2}\)sđ cung \(BE)\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung chắn cung \(BE\)).
\(\begin{array}{l} \Rightarrow \Delta AEB \backsim \Delta ABF(g - g)\\ \Rightarrow \dfrac{{AE}}{{AB}} = \dfrac{{AB}}{{AF}}\end{array}\)
\( \Leftrightarrow FA.EA = A{B^2}\) (đpcm)
Vì \(\Delta AEB \backsim \Delta ABF\,\,\,\left( {cmt} \right)\)\( \Rightarrow \dfrac{{BE}}{{BF}} = \dfrac{{AB}}{{AF}}\) (các cặp cạnh tương ứng tỉ lệ)
Ta có: \(\angle ACE = \angle AFC\,\,\)\(( = \dfrac{1}{2}\) sđ cung \(EC)\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung EC)
\(\begin{array}{l} \Rightarrow \Delta ACE \backsim \Delta AFC\,\,(g - g)\\ \Rightarrow \dfrac{{EC}}{{FC}} = \dfrac{{AC}}{{FA}} = \dfrac{{AB}}{{FA}}\\ \Rightarrow \dfrac{{BE}}{{BF}} = \dfrac{{EC}}{{FC}}\,\,\left( { = \dfrac{{AB}}{{AF}}} \right)\end{array}\)
\( \Rightarrow BE.FC = BF.EC\,\) (đpcm)
c) Chứng minh OCKA là hình thang cân.
Ta có: \(CK//OA\,\,\left( {gt} \right) \Rightarrow ACKA\) là hình thang (định nghĩa).
Lại có: \(\angle OKC = \angle AOK\,\,\,(so\,\,le\,\,trong)\)
Vì \(AB \bot OB\,\,\left( {cm\,\,a} \right),\,\,OF \bot OB\,\,\left( {gt} \right)\) \( \Rightarrow KF//AB\)(từ vuông góc đến song song)
\(\begin{array}{l} \Rightarrow \angle BAO\,\, = \angle AOK\,\,\,\left( {so\,\,le\,\,trong} \right)\\ \Rightarrow \angle OKC = \angle BAO\,\,\left( { = \angle AOK} \right)\end{array}\)
Mặt khác \(\angle BAO = \angle OAC\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow \angle OKC = \angle OAC\,\,\left( { = \angle BAO} \right)\)
\( \Rightarrow AKCO\) là tứ giác nội tiếp (dhnb).
Hình thang nội tiếp tứ giác là hình thang cân \( \Rightarrow AKCO\) là hình thang cân (đpcm)
Nguồn sưu tầm
soanvan.me
