Video hướng dẫn giải
Giải các phương trình:
LG a.
\(3{x^2} + 2x - 1 = 0\) ;
Phương pháp giải:
- Biến đổi phương trình về dạng phương trình tích.
- Tìm \(x\)
- Kết luận
Giải chi tiết:
\(3{x^2} + 2x - 1 = 0\)
\(⇔3{x^2}- 3 + 2x + 2 = 0\)
\(⇔3({x^2}– 1) + 2(x + 1) = 0\)
\(⇔3(x - 1)(x + 1) + 2(x + 1) = 0\)
\(⇔(x + 1)(3x - 3 + 2) =0\)
\(⇔(x + 1)(3x - 1)=0\)
\(⇔\left[ {\matrix{{x + 1 = 0} \cr {3x - 1 = 0} \cr} } \right.\)
\(⇔\left[ {\matrix{{x = - 1} \cr {x = \dfrac{1}{3}} \cr} } \right.\)
Vậy \(S = \left\{ { - 1;\dfrac{1}{3}} \right\}\)
LG b.
\(\dfrac{{x - 3}}{{x - 2}} + \dfrac{{x - 2}}{{x - 4}} = 3\dfrac{1}{5}\)
Phương pháp giải:
- Tìm điều kiện xác định.
- Qui đồng khử mẫu.
- Rút gọn rồi tìm nghiệm \(x\).
- Đối chiếu với điều kiện xác định rồi kết luận nghiệm.
Giải chi tiết:
\(\dfrac{{x - 3}}{{x - 2}} + \dfrac{{x - 2}}{{x - 4}} = 3\dfrac{1}{5}\)
ĐKXĐ: \(x \ne 2;x \ne 4\)
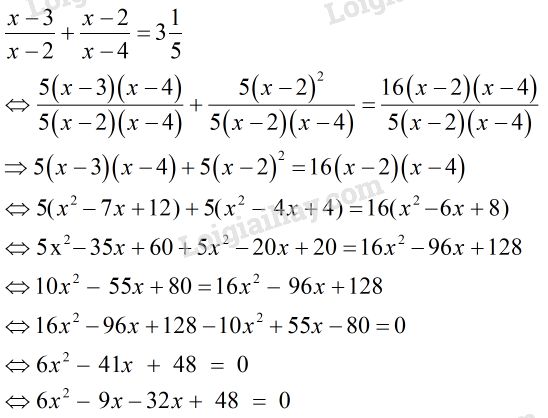
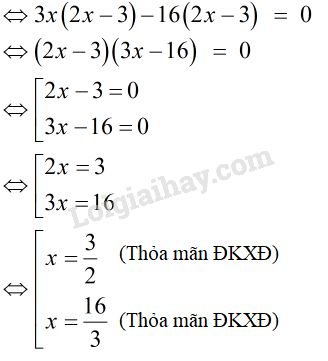
Vậy phương trình có tập nghiệm: \(S =\left\{ {\dfrac{3}{2};\dfrac{{16}}{3}} \right\}\)
soanvan.me
