Đề bài
Hình 75 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo \((OA = OB)\). Hãy so sánh tổng thể tích của hai hình nón và thể tích hình trụ.
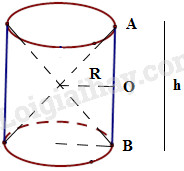
Hình 75
Phương pháp giải - Xem chi tiết
+ Tính thể tích hình nón có bán kính \(R\) và chiều cao \(h\) là \(V = \dfrac{1}{3}\pi {R^2}h\)
+ Tính thể tích hình trụ có bán kính \(R\) và chiều cao \(h\) là \(V = \pi {R^2}h\)
Lời giải chi tiết

Gọi \({V_1},{V_2}\) là thể tích của hai hình nón;
\({h_1}\) là chiều cao hình nón;
\({R_1}\) là bán kính hình nón.
Từ giả thiết ta có
\({V_1} = {V_2}\) vì \(OA = OB\); diện tích đáy bằng nhau
Suy ra \({V_n} =V_1+V_2=2V_1\) và \({R_1} = R;{h_1} = OA = OB = \dfrac{h}{2};\)
Theo công thức tính thể tích hình nón : \({V_n} = 2.V_1=2 \cdot \dfrac{1}{3}\pi {R^2} \cdot {h_1}\)
Do đó \({V_n} =2 \cdot \dfrac{1}{3}\pi {R^2}\dfrac{h}{2}= \dfrac{1}{3}\pi {R^2}{h}\) (1)
Theo công thức tính thể tích hình trụ : \({V_T} = \pi {R^2}h.\) (2)
So sánh (1) và (2), ta có tổng thể tích hai hình nón bằng \( \dfrac{1}{3}\) thể tích hình trụ.
soanvan.me
