Đề bài
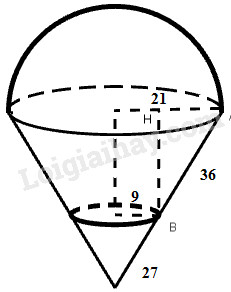
Một cái xô bằng inốc có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 77 (đơn vị: cm).
a) Hãy tính diện tích xung quanh của xô
b) Khi xô chứa đầy hóa chất thì dung tích của nó là bao nhiêu ?
Phương pháp giải - Xem chi tiết
Hình nón cụt có bán kính hai đáy \({r_1};{r_2}\), chiều cao \(h\) và đường sinh \(l\) thì
- Diện tích xung quanh hình nón cụt \({S_{xq}} = \pi \left( {{r_1} + {r_2}} \right)l\)
- Thể tích hình nón cụt \(V = \dfrac{1}{3}\pi h\left( {r_1^2 + r_2^2 + {r_1}{r_2}} \right)\)
Lời giải chi tiết

Gọi \(l\) là đường sinh của xô hình nón cụt, \({r_1}\) và \({r_2}\) là hai bán kính và \({S_{xq}}\) là diện tích xung quanh, \(V\) là thể tích hình nón cụt.
Theo kích thước ta có \(l = 36cm;{r_1} = 9cm;{r_2} = 21cm\)
a) \({S_{xq}} = \pi \left( {{r_1} + {r_2}} \right).l = \pi \left( {9 + 21} \right).36\)\( = 1080\pi \left( {c{m^2}} \right)\)
b) Dung tích của xô chứa đầy hóa chất bằng thể tích của xô, nên theo công thức
\(V = \dfrac{1}{3}\pi h\left( {r_1^2 + r_2^2 + {r_1}{r_2}} \right)\) ta cần tính \(h\).
Xét tam giác vuông \(AHB,\) ta có \(HA = 21 - 9 = 12cm;HB = h.\)
\(h = \sqrt {A{B^2} - H{A^2}} = \sqrt {{{36}^2} - {{12}^2}}\)\( = 24\sqrt 2 \left( {cm} \right)\)
Vậy \(V = \dfrac{1}{3}\pi .h\left( {{r_1}^2 + {r_2}^2 + {r_1}.{r_2}} \right) \)\(= \dfrac{1}{3}\pi .24\sqrt 2 \left( {{9^2} + {{21}^2} + 9.21} \right)\)\( = 5688\sqrt 2 \pi \,\left( {c{m^3}} \right)\)
soanvan.me
