Bài 14 trang 139 Vở bài tập toán 9 tập 2

Đề bài

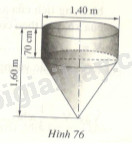
Một dụng cụ gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho ở hình 76. Hãy tính:

a) Thể tích của dụng cụ này

b) Diện tích mặt ngoài của dụng cụ (không kể nắp đậy).

Lời giải chi tiết

Ta gọi \({h_1}\) là chiều cao hình trụ, \({h_2}\) là chiều cao hình nón và \({R_1};{R_2}\) lần lượt là bán kính đáy của hình trụ và hình nón.\({V_T};{V_n}\) và \({S_{xqT}};{S_{xqn}}\) là các thể  tích và diện tích mặt ngoài của hình trụ và hình nón. \(V\) và \(S\) lần lượt là thể tích và diện tích của dụng cụ cần tìm.

\(70cm = 0,7m\)

Theo kích thước đã cho ta có : \({h_1} = 0,7m;\) \({h_2} = 0,9m\); \({R_1} = {R_2} = 0,7m.\)

a) Thể tích hình trụ \({V_1} = \pi R_1^2{h_1} = \pi .0,{7^2}.0,7 = 0,343\pi\)\( \left( {{m^3}} \right)\)

Thể tích hình nón \({V_2} = \dfrac{1}{3}\pi R_2^2{h_2} = \dfrac{1}{3}\pi 0,{7^2}.0,9 \)\(= 0,147\pi \left( {{m^3}} \right)\)

Thể tích dụng cụ này là \(V = {V_1} + {V_2} = 0,343\pi  + 0,147\pi\)\(  = 0,49\pi \left( {{m^3}} \right)\)

b) Diện tích xung quanh hình trụ là \({S_1} = 2\pi {R_1}{h_1} = 2\pi .0,7.0,7 \)\(= 0,98\pi \left( {{m^2}} \right)\)

Gọi \(l\) là đường sinh hình nón thì \(l = \sqrt {R_2^2 + h_2^2}  = \sqrt {0,{7^2} + 0,{9^2}} \)\( = \dfrac{{\sqrt {130} }}{{10}}m\)

Nên diện tích xung quanh hình nón là \({S_2} = \pi {R_2}l = \pi .0,7.\dfrac{{\sqrt {130} }}{{10}} = \dfrac{{7\pi \sqrt {130} }}{{100}}\)\(\left( {{m^2}} \right)\) 

Diện tích mặt ngoài của dụng cụ là \(S = {S_1} + {S_2} = 0,98\pi  + \dfrac{{7\pi \sqrt {130} }}{{100}}\)\( \approx 5,58\,\left( {{m^2}} \right)\)

soanvan.me