Đề bài
Một hình nón được đặt vào bên trong một hình lập phương như hình 72 (cạnh của hình lập phương bằng 1). Hãy tính:
a) Bán kính đáy của hình nón
b) Độ dài đường sinh
Phương pháp giải - Xem chi tiết
a) Đường tròn nội tiếp hình vuông cạnh \(a\) có bán kính \(r = \dfrac{a}{2}\)
b) Tính đường sinh dựa vào định lý Pytago trong tam giác vuông \(AOI.\)
Lời giải chi tiết
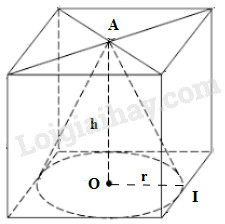
Gọi \(r\) là bán kính; \(l\) là đường sinh.
a) Ta có đáy hình nón nội tiếp của đáy hình lập phương cạnh bằng 1 \( \Rightarrow \) \(r = \dfrac{1}{2}.\)
b) Chiều cao hình lập phương \(h = AO = 1.\)
Xét tam giác \(OAI\) vuông tại \(O\), \(l = AI,r = OI.\)
Ta có : \({l^2} = A{O^2} + O{I^2} = {1^2} + 0,{5^2}\)
Vậy \(l = \sqrt {{h^2} + {r^2}} = \sqrt {{1^2} + 0,{5^2}} = \dfrac{{\sqrt 5 }}{2}\)
soanvan.me
