Đề bài
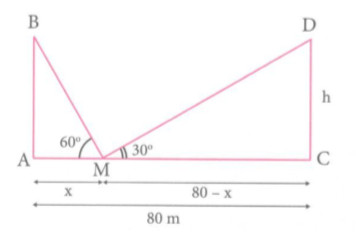
Hai trụ điện cùng chiều cao được dựng thẳng đứng hai bên lề đối điện một đại lộ rộng 80 m. Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là \({60^o}\) và \({30^o}\). Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.
Phương pháp giải - Xem chi tiết
Áp dụng hệ thức về cạnh và góc trong tam giác vuông để lập phương trình tính AM từ đó tính chiều cao của trụ điện.
Lời giải chi tiết
Gọi AM = x (m) \( \Rightarrow \) MC = BC – AM = 80 – x (m)
Xét tam giác BAM vuông tại A: \(AB = AM.\tan \widehat {AMB} = x.\tan {60^o} = x.\sqrt 3 \) (m)
Xét tam giác DCM vuông tại C: \(CD = MC.\tan \widehat {CMD} = \left( {80 - x} \right).\tan {30^o} = \dfrac{{\sqrt 3 }}{3}\left( {80 - x} \right)\) (m)
Vì hai trụ điện cùng chiều cao \( \Rightarrow \)AB = CD
\( \Rightarrow x.\sqrt 3 = \dfrac{{\sqrt 3 }}{3}\left( {80 - x} \right) \)
\(\Leftrightarrow 3x = 80 - x \)
\(\Leftrightarrow 4x = 80 \)
\(\Leftrightarrow x = 20\)(m)
\( \Rightarrow AM = 20\,\,m\,\,;\)
\(\,\,MC = 80 - 20 = 60\,\,m\,\,;\)
\(\,\,AB = CD = 20\sqrt 3 \approx 34,64\,\,m\)
soanvan.me
