Đề bài
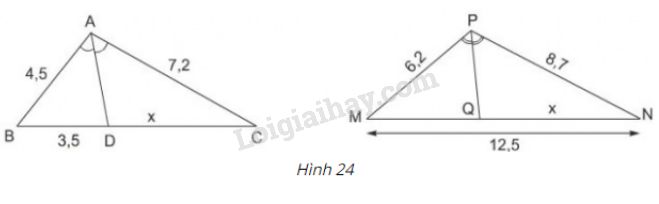
Tính \(x\) trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Tính chất đường phân giác của tam giác, tính chất của tỉ lệ thức.
Lời giải chi tiết
a) \(AD\) là tia phân giác góc \(A\) của \(∆ABC\) (gt) nên áp dụng tính chất của đường phân giác trong tam giác ta có:
\(\dfrac{BD}{AB} = \dfrac{DC}{AC}\)
\(\Rightarrow DC = \dfrac{BD.AC}{AB}= \dfrac{3,5.7,2}{4,5}\)
\(\Rightarrow x = 5,6\)
b) \(PQ\) là đường phân giác góc \(P\) của \(∆PMN\) (gt) nên
\(\dfrac{MQ}{MP}= \dfrac{NQ}{NP}\) (tính chất đường phân giác của tam giác)
Hay \(\dfrac{MQ}{6,2} = \dfrac{x}{8,7}\)
Có: \(MN=MQ+x=12,5\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\Rightarrow \dfrac{x}{8,7} = \dfrac{MQ}{6,2} = \dfrac{x + MQ}{8,7+ 6,2}= \dfrac{12,5}{14,9}\)
\( \Rightarrow x = \dfrac{{12,5.8,7}}{{14,9}} \approx 7,3\)
soanvan.me
