Đề bài
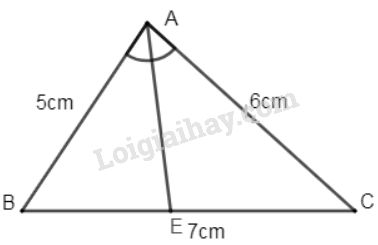
Tam giác \(ABC\) có \(AB= 5cm, AC= 6cm, BC= 7cm.\) Tia phân giác của góc \(BAC\) cắt \(BC\) tại \(E\). Tính các đoạn \(EB, EC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Tính chất đường phân giác của tam giác, tính chất của dãy tỉ số bằng nhau.
Lời giải chi tiết
Vì \(AE\) là đường phân giác của tam giác ABC nên
\(\dfrac{EB}{AB} = \dfrac{EC}{AC}\) (tính chất đường phân giác của tam giác)
\( \Rightarrow\) \(\dfrac{EB}{5} = \dfrac{EC}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{EB}{5} = \dfrac{EC}{6} = \dfrac{EB+EC}{5+6} = \dfrac{BC}{11}=\dfrac{7}{11}\)
\( \Rightarrow EB = \dfrac{5.7}{11} =\dfrac{35}{11}\) cm
\(EC = \dfrac{6.7}{11} =\dfrac{42}{11}\) cm
