Đề bài
Cho tam giác ABC vuông tại A, \(\widehat B = \alpha \) , AB= 6 cm. Biết \(\tan \alpha = \dfrac{5}{{12}}.\)
Hãy tính :
a) Cạnh AC ; b) Cạnh BC.
Phương pháp giải - Xem chi tiết
- Dựa vào tỉ số lượng giác : \(\tan \alpha = \dfrac{{cạnh\,\,đối}}{{cạnh\,\,kề}}\) và giá trị \(\tan \alpha \); độ dài cạnh \(AB\) đã biết để tìm giá trị của cạnh \(AC.\)
- Dùng định lí Pi-ta-go để tìm độ dài cạnh BC khi biết độ dài hai cạnh còn lại của tam giác vuông.
Lời giải chi tiết
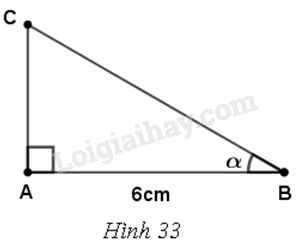
a) Theo định nghĩa các tỉ số lượng giác, ta có :
\(\tan \alpha = \dfrac{{AC}}{{AB}}\)
Suy ra \(AC = AB.\tan \alpha \)\(= 6 \cdot \dfrac{5}{{12}} = 2,5\left( {cm} \right).\)
b) Trong tam giác vuông \(ABC,\) theo định lí Pi-ta-go ta có :
\(BC = \sqrt {A{C^2} + A{B^2}} \)\(= \sqrt {{6^2} + 2,{5^2}} = 6,5\left( {cm} \right).\)
soanvan.me
