Đề bài
Ở hình dưới, cho biết AB là tiếp tuyến của đường tròn (O) tại B. Tính bán kính r của đường tròn (O).
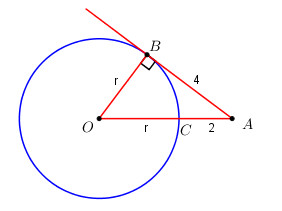
Phương pháp giải - Xem chi tiết
Sử dụng định lí Pytago trong tam giác vuông.
Lời giải chi tiết
Do AB là tiếp tuyến của \(\left( O \right) \Rightarrow OB \bot AB\) tại B \( \Rightarrow \Delta OAB\) vuông tại O.
Áp dụng định lí Pytago trong tam giác vuông OAB ta có :
\(\begin{array}{l}O{B^2} + A{B^2} = O{A^2}\\ \Leftrightarrow {r^2} + {4^2} = {\left( {r + 2} \right)^2}\\ \Leftrightarrow {r^2} + 16 = {r^2} + 4r + 4\\ \Leftrightarrow 4r = 12 \Leftrightarrow r = 3\,\,\left( {cm} \right)\end{array}\)
Vậy bán kính của đường tròn \(\left( O \right)\) là \(r = 3cm\).
soanvan.me
