Đề bài
Ở hình dưới, biết MB, MC là hai tiếp tuyến của đường tròn (O) tại B và C, \(\widehat {COB} = {130^o}\). Tính số đo góc CMB.
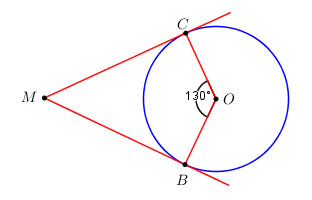
Phương pháp giải - Xem chi tiết
Sử dụng định lí : tiếp tuyến của đường tròn tại 1 điểm thì vuông góc với bán kính đi qua điểm đó và định lí tổng 4 góc của tứ giác bằng 3600.
Lời giải chi tiết
Vì MB, MC là tiếp tuyến của \(\left( O \right) \Rightarrow \left\{ \begin{array}{l}MB \bot OB \Rightarrow \widehat {OBM} = {90^0}\\MC \bot OC \Rightarrow \widehat {OCM} = {90^0}\end{array} \right.\).
Xét tứ giác OBMC có : \(\widehat {OBM} + \widehat {BMC} + \widehat {OCM} + \widehat {BOC} = {360^0}\) (tổng 4 góc của tứ giác)
\(\begin{array}{l} \Rightarrow {90^0} + \widehat {BMC} + {90^0} + {130^0} = {360^0}\\ \Rightarrow {310^0} + \widehat {BMC} = {360^0}\\ \Rightarrow \widehat {BMC} = {50^0}\end{array}\).
soanvan.me
