Đề bài
Ở hình dưới, AB là tiếp tuyến chung ngoài của đường tròn (O) và (O’). Biết đoạn nối tâm \({\rm{OO}}' = 45cm,OA = 19cm,\) \(O'B = 10cm\). Tính AB.
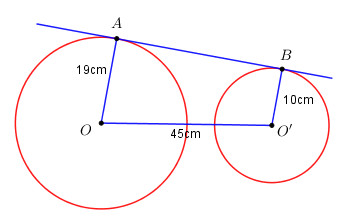
Phương pháp giải - Xem chi tiết
+) Kẻ \(O'H \bot OA\,\left( {H \in OA} \right)\), chứng minh \(O'HAB\) là hình chữ nhật (Tứ giác có 3 góc vuông) \( \Rightarrow O'H = AB\).
+) Áp dụng định lí Pytago trong tam giác vuông tính \(O'H\), từ đó suy ra độ dài \(AB\).
Lời giải chi tiết
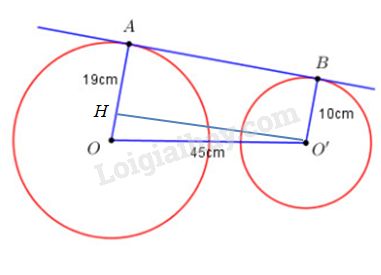
Kẻ \(O'H \bot OA\,\left( {H \in OA} \right)\).
Xét tứ giác \(O'HAB\) ta có : \(\angle O'BA = \angle O'HA = \angle HAB = {90^0} \Rightarrow \) Tứ giác \(O'HAB\) là hình chữ nhật (Tứ giác có 3 góc vuông) \( \Rightarrow O'H = AB\) và \(AH = O'B = 10cm\).
Ta có : \(OH = OA - AH = 19 - 10 = 9\,\,\left( {cm} \right)\).
Áp dụng định lí Pytago trong tam giác vuông \(OO'H\) ta có :
\(O'H = \sqrt {OO{'^2} - O{H^2}} = \sqrt {{{45}^2} - {9^2}} \)\(\, = \sqrt {1944} = 18\sqrt 6 \,\,\left( {cm} \right)\).
Vậy \(AB = 18\sqrt 6 cm\).
soanvan.me
