Đề bài
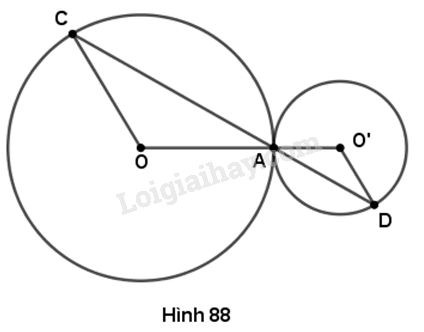
Trên hình 88, hai đường tròn tiếp xúc nhau tại A, ba điểm C, A, D thẳng hàng. Chứng minh rằng OC // O’D.
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat C = \widehat D\) qua hai góc trung gian \(\widehat {OAC}\) và \(\widehat {O'AD}\).
Lời giải chi tiết
Tam giác \(OAC\) có \(OA = OC\) (bán kính) nên là tam giác cân, suy ra \(\widehat C = \widehat A.\) (1)
Tam giác \(O'AD\) có \(O'A = O'D\) (bán kính) nên là tam giác cân, suy ra \(\widehat D = \widehat {O'AD}\) (2)
Hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc nhau tại \(A\) nên ba điểm \(A,C,D\) thẳng hàng, do đó \(\widehat {OAC} = \widehat {O'AD}\) (đối đỉnh).
Từ (1), (2), (3) suy ra \(\widehat C = \widehat D.\)
Hai góc \(C,D\) so le trong và bằng nhau nên \(OC//O'D.\)
soanvan.me
