Đề bài
a) Tâm của các đường tròn bán kính 1cm tiếp xúc ngoài với đường tròn tâm O bán kính 3cm nằm trên đường nào ?
b) Tâm của các đường tròn bán kính 1cm tiếp xúc trong với đường tròn tâm O bán kính 3cm nằm trên đường nào ?
Phương pháp giải - Xem chi tiết
Áp dụng kiến thức : Hai đường tròn tiếp xúc nhau, tiếp xúc ngoài khi \(OO’ = R + r;\) tiếp xúc trong khi \(OO’ = R – r > 0.\)
Lời giải chi tiết
a)
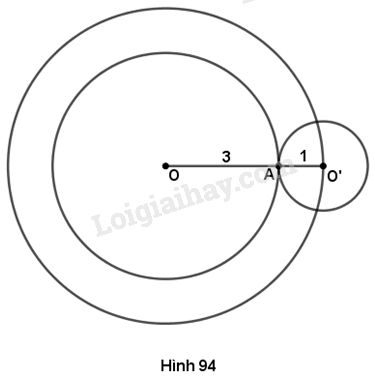
(h. 94) Gọi \(O'\) là tâm của một đường tròn bất kì bán kính \(1cm\) tiếp xúc ngoài với đường tròn \(\left( {O;3cm} \right).\)
Hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài nên \(OO' = OA + O'A = 4\left( {cm} \right).\)
Điểm \(O'\) cách điểm \(O\) cố định một khoảng \(4cm\) nên \(O'\) nằm trên đường tròn tâm \(O\) bán kính \(4cm.\)
Vậy tâm của các đường tròn bán kính \(1cm\) tiếp xúc ngoài với đường tròn \(\left( {O;3cm} \right)\) nằm trên đường tròn \(\left( {O;4cm} \right).\)
b)
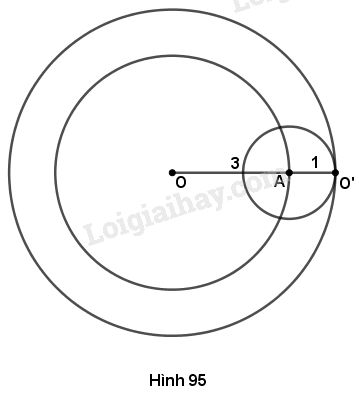
Gọi \(O'\) là tâm của một đường tròn bất kì bán kính \(1cm\) tiếp xúc trong với đường tròn \(\left( {O;3cm} \right).\)
Hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc trong nên \(OO' = OA - O'A = 2\left( {cm} \right).\)
Điểm \(O'\) cách điểm \(O\) cố định một khoảng \(2cm\) nên \(O'\) nằm trên đường tròn tâm \(O\) bán kính \(2cm.\)
Vậy tâm của các đường tròn bán kính \(1cm\) tiếp xúc trong với đường tròn \(\left( {O;3cm} \right)\) nằm trên đường tròn \(\left( {O;2cm} \right).\)
soanvan.me
