Đề bài
Cho đường tròn tâm \(O\) bán kính \(OA\) và đường tròn đường kính \(OA\).
a) Hãy xác định vị trí tương đối của hai đường tròn.
b) Dây \(AD\) của đường tròn lớn cắt đường tròn nhỏ ở \(C\). Chứng minh rằng \(AC=CD\).
Phương pháp giải - Xem chi tiết
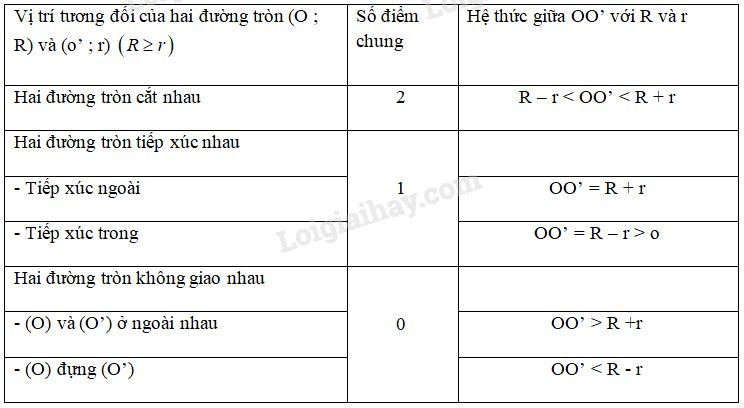
Tìm \({\rm{OO}}'\) và \(R+r\) hoặc \(R - r\) rồi dùng bảng sau:
Lời giải chi tiết
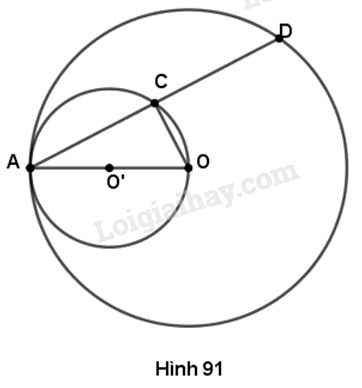
a) Gọi \(O'\) là trung điểm của \(OA.\) Đường tròn \(\left( O \right)\) có bán kính là \(OA,\) đường tròn \(\left( {O'} \right)\) có bán kính là \(O'A.\)
Ta có \({\rm{OO}}' = OA - O'A\) nên hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) có vị trí tiếp xúc trong.
b) Tam giác \(ACO\) nội tiếp đường tròn đường kính \(AO\) nên \(\widehat {ACO} = {90^o}.\)
Tam giác \(AOD\) có \(OA = OD\) (bán kính) nên là tam giác cân tại \(O,\) \(OC\) là đường cao nên cũng là đường trung tuyến, do đó \(AC = CD.\)
soanvan.me
