Đề bài
Cho hai đường tròn (O ; 3cm) và (O’ ; 2cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn, \(B \in \left( O \right),C \in \left( {O'} \right)\). Gọi I là giao điểm của đường thẳng BC và OO’. Tính độ dài O’I.
Phương pháp giải - Xem chi tiết
Chứng minh đường thẳng \(O'C\) song song với \(OB\) rồi áp dụng định lí Ta-lét.
Lời giải chi tiết
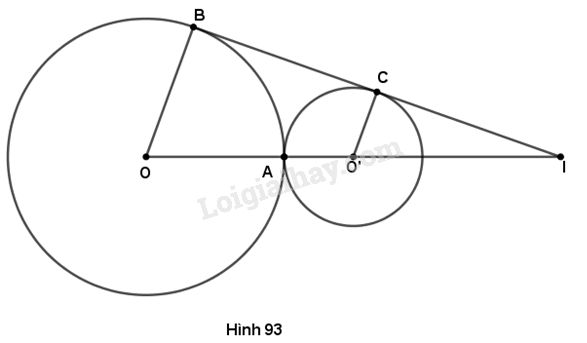
Ta có \(O'C//OB\) (vì cùng vuông góc \(BC\))
Theo định lí Ta-lét ta có :
\(\dfrac{{O'I}}{{OI}} = \dfrac{{O'C}}{{OB}} = \dfrac{{IC}}{{IB}}.\)
Suy ra \(\dfrac{{O'I}}{{OI - O'I}} = \dfrac{{O'C}}{{OB - O'C}},\) do đó \(\dfrac{{O'I}}{{OO'}} = 2.\)
Vậy \(O'I = 2.OO' = 2.5 = 10\left( {cm} \right).\)
soanvan.me
