Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao \(h\) và đáy lần lượt là:
LG a
Hình vuông cạnh \(a\);
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.
Lời giải chi tiết:
Bài toán này chủ yếu là tính được diện tích đáy và chu vi đáy, do đó ta chỉ cần vẽ các đáy của hình lăng trụ đứng cho mỗi trường hợp ở trên (h.99)
(h.99a)
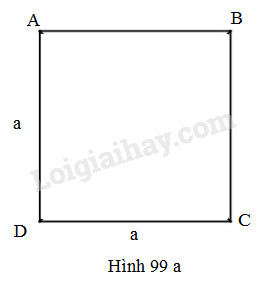
\({S_{đáy}} =S_{ABCD}= {a^2}\)
\({S_{xq}} = 2p.h = 4.a.{\text{ }}h\)
\({S_{tp}} = {S_{xq}} + 2{S_{đáy}} = 4ah + 2{a^2}\)
\(V = {S_{đáy}}h = {a^2}.h\)
LG b
Tam giác đều cạnh \(a\);
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.
Lời giải chi tiết:
(h.99b)
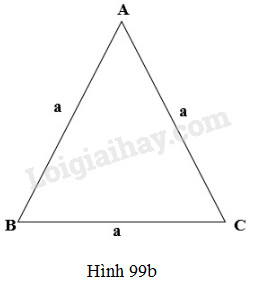
\({S_{đáy}} =S_{ABC} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
\({S_{xq}} = 2p.h = 3a.h\)
\({S_{tp}} = {S_{xq}} + 2{S_{đáy}} =2.\dfrac{{{a^2}\sqrt 3 }}{4}+3ah\)\( = \frac{1}{2}\left( {{a^2}\sqrt 3 + 6ah} \right)\)
\(V = {S_{đáy}}h = \dfrac{{{a^2}\sqrt 3 }}{4}.h = \dfrac{{{a^2}h\sqrt 3 }}{4}\)
LG c
Lục giác đều cạnh \(a\);
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.
Lời giải chi tiết:
(h99c)
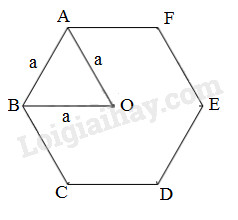
\(S_{OAB}= \dfrac{{{a^2}\sqrt 3 }}{4}\)
\(\Rightarrow {S_{đáy}} =6. \dfrac{{{a^2}\sqrt 3 }}{4}\)\(= \dfrac{{3{a^2}\sqrt 3 }}{2}\)
\({S_{xq}} = 2p.h = 6a.h\)
\({S_{tp}} = {S_{xq}} + 2{S_{đáy}} = 6ah + 2.\dfrac{{3{a^2}\sqrt 3 }}{2} \)\(= 6ah + 3{a^2}\sqrt 3 \)\(\, = 3a\left( {2h + a\sqrt 3 } \right)\)
\(V = {S_{đáy}}h = \dfrac{{3{a^2}\sqrt 3 }}{2}.h = \dfrac{{3{a^2}h\sqrt 3 }}{2}\)
LG d
Hình thang cân, đáy lớn là \(2a\), các cạnh còn lại bằng \(a\);
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.
Lời giải chi tiết:
(h99d)
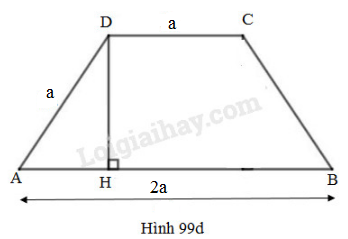
Kẻ thêm đường cao \(DH\) của đáy \(ABCD\) , ta có:
\(AH = \dfrac{1}{2}\left( {AB - CD} \right) \)\(= \dfrac{1}{2}\left( {2a - a} \right) = \dfrac{a}2\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(ADH\), ta có:
\(DH = \sqrt {A{D^2} - A{H^2}} \)\(= \sqrt {{{{a}}^2} - {\dfrac{a^2}4}} =\dfrac{{a\sqrt 3 }}{2}\)
\({S_{đáy}}=S_{ABCD} = \dfrac{1}{2}\left( {AB + CD} \right).DH\)\(=\dfrac{1}2. \left( {2a + a} \right).\dfrac{{a\sqrt 3 }}{2} \)\(= \dfrac{{3{a^2}\sqrt 3 }}{4}\)
\({S_{xq}}= 2ph = (2a + a +a +a). h \)\(\,= 5ah\).
\({S_{tp}} = {S_{xq}} + 2{S_đ} = 5ah + 2.\dfrac{{3{a^2}\sqrt 3 }}{4} \)\(\,= 5ah + \dfrac{{3{a^2}\sqrt 3 }}{2}\)
\(V = {S_{đáy}}.h = \dfrac{{3{a^2}\sqrt 3 }}{4}.h = \dfrac{{3{a^2}h\sqrt 3 }}{4}\)
LG e
Hình thoi có hai đường chéo là \(6a\) và \(8a\).
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.
Lời giải chi tiết:
(h.99e)
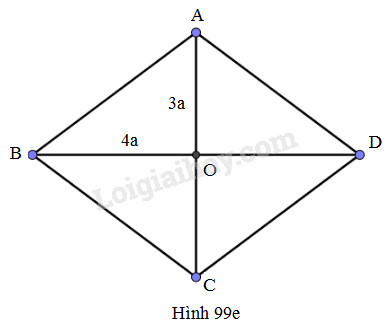
\(AC=6a\Rightarrow OA=3a\)
\(BD=8a\Rightarrow OB=4a\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(OAB\), ta có:
\(AB = \sqrt {O{A^2} + O{B^2}} \) \(= \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} \) \(= \sqrt {25{a^2}} = 5a\)
\({S_{đáy}} =S_{ABCD}=\dfrac{1}{2}AC.BD\)\(= \dfrac{1}{2}.6a.8a = 24{a^2}\)
\(S_{xq}= 2ph =4.AB.h=4.5a.h = 20ah\)
\({S_{tp}} = {S_{xq}} + {S_{đáy}} \)\(\,= 20ah + 2.24a^2 = 20ah + 48{a^2}\)
\(V = {S_{đáy}}.h =24{a^2}.h\)
soanvan.me
