Đề bài
Câu 1: (3 điểm) Cho hình hộp chữ nhật ABCD.EFGH (h.107). Hãy chọn khẳng định đúng.
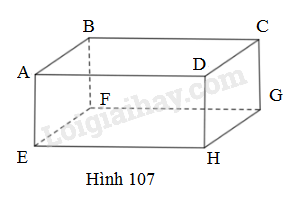
a) Mặt phẳng (ABFE) song song với mặt phẳng:
I. (ABCD); II. (BCGF)
III. (ADHE) IV. (DCGH)
b) Đường thẳng AB song song với đường thẳng:
I. EH; II. FG
III. HG IV. BC
c) Đường thẳng AE vuông góc với mặt phẳng:
I. (BCGF); II. (ABCD)
III. (DCGH) IV. (ADHE)
Câu 2: (3 điểm)
Lăng trụ đứng ABCD.EFGH có đáy ABCD là một hình vuông, đường cao \(AE=h=8cm\); đường chéo của mặt bên \(AF = d = 10cm\) (h.108)
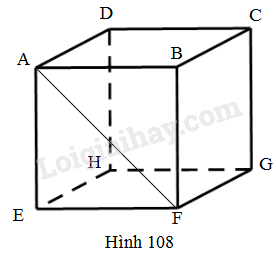
a) Tính diện tích toàn phần của lăng trụ
b) Tính thể tích của lăng trụ
Câu 3: (4 điểm) Hình chóp tam giác đều S.ABC có cạnh đáy là \(a = 6cm,\) cạnh bên là \(b = 8cm\) (h.109)

a) Tính diện tích đáy của hình chóp
b) Tính diện tích xung quanh và diện tích toàn phần của hình chóp
c) Tính thể tích hình chóp
(Các kết quả lấy với hai chữ số thập phân)
Lời giải chi tiết
Câu 1:
Phương pháp
Sử dụng tính chất hình hộp chữ nhật.
Đường thẳng d vuông góc với mặt phẳng (P) nếu d vuông góc với hai đường thẳng cắt nhau nằm trong (P)
LG
a) Mặt phẳng (ABFE) song song với mặt phẳng (DCGH) vì các mặt đối nhau của hình hộp chữ nhật song song với nhau
Chọn IV.
b) Vì ABFE là hình chữ nhật nên AB//FE
Vì EFGH là hình chữ nhật nên EF//HG
Suy ra AB//HG
Chọn II
c) Đường thẳng AE vuông góc với mặt phẳng (ABCD) vì trong hình hộp chữ nhật thì cạnh bên luôn vuông góc với mặt phẳng đáy.
Câu 2:
Phương pháp
a) Diện tích toàn phần \({S_{tp}} = 2{S_{đáy}} + {S_{xq}}\)
b) Thể tích lăng trụ \(V = {S_{đáy}}.h\) với \(h\) là chiều cao lăng trụ
LG
a) Xét tam giác AEF vuông tại E, theo định lí Py-ta-go ta có:
\(\begin{array}{l}A{F^2} = A{E^2} + E{F^2}\\ \Rightarrow E{F^2} = A{F^2} - A{E^2}\\ \Rightarrow E{F^2} = {10^2} - {8^2} = 36\\ \Rightarrow EF = 6cm\end{array}\)
Diện tích 1 đáy của lăng trụ là: \(S = {S_{EFGH}} = E{F^2} = 36c{m^2}\)
Diện tích xung quanh của lăng trụ là: \({S_{xq}} = 2p.h = 6.4.8 = 192c{m^2}\)
Diện tích toàn phần: \({S_{tp}} = 2S + {S_{xq}} \)\(= 2.36 + 192 = 264c{m^2}\)
b) Thể tích lăng trụ: \(V = {S_{EFGH}}.AE = 36.8 = 288c{m^3}\)
Câu 3:
Phương pháp
a) Diện tích tam giác bằng nửa tích của đáy với chiều cao tương ứng
b) Diện tích xung quanh hình chóp \({S_{xq}} = p.d\) với \(p\) là nửa chu vi đáy và \(d\) là trung đoạn của hình chóp
Diện tích toàn phần \({S_{tp}} = {S_{đáy}} + {S_{xq}}\)
c) Thể tích hình chóp \(V = \dfrac{1}{3}{S_{đáy}}.h\) với \(h\) là chiều cao hình chóp
LG
a) Tam giác ABC đều có \(O\) là trọng tâm và E là trung điểm cạnh AB nên suy ra \(CE \bot AB\) và \(AE = \dfrac{1}{2}AB = \dfrac{1}{2}.6 = 3cm\)
Xét tam giác ACE vuông tại E, theo định lí Py-ta-go ta có:
\(\begin{array}{l}C{E^2} + A{E^2} = A{C^2}\\ \Rightarrow C{E^2} = A{C^2} - A{E^2}\\ \Rightarrow C{E^2} = {6^2} - {3^2} = 36 - 9 = 27\\ \Rightarrow CE = \sqrt {27} cm\end{array}\)
Khi đó, diện tích tam giác ABC là: \({S_{ABC}} = \dfrac{1}{2}CE.AB = \dfrac{1}{2}.\sqrt {27} .6\) \( = 3\sqrt {27} \approx 15,59c{m^2}\)
b) Xét tam giác ASE vuông tại E, theo định lí Py-ta-go ta có:
\(\begin{array}{l}S{E^2} + A{E^2} = S{A^2}\\ \Rightarrow S{E^2} = S{A^2} - A{E^2}\\ \Rightarrow S{E^2} = {8^2} - {3^2} = 64 - 9 = 55\\ \Rightarrow SE = \sqrt {55} cm\end{array}\)
Nửa chu vi tam giác ABC là: \(\dfrac{1}{2}\left( {6 + 6 + 6} \right) = 9cm\)
Diện tích xung quanh hình chóp \({S_{xq}} = p.d = 9.\sqrt {55} \approx 66,75c{m^2}\)
Diện tích toàn phần \({S_{tp}} = {S_{ABC}} + {S_{xq}} \approx 15,59 + 66,75 = 82,34c{m^2}\)
c) Vì \(O\) là trọng tâm tam giác ABC nên \(OC = \dfrac{2}{3}CE = \dfrac{2}{3}.\sqrt {27} = 2\sqrt 3 cm\)
Xét tam giác SCO vuông tại O, theo định lí Py-ta-go ta có:
\(\begin{array}{l}S{C^2} = C{O^2} + S{O^2}\\ \Rightarrow S{O^2} = S{C^2} - C{O^2}\\ \Rightarrow S{O^2} = {8^2} - {\left( {2\sqrt 3 } \right)^2} = 52\\ \Rightarrow SO = \sqrt {52} cm\end{array}\)
Thể tích hình chóp: \(V = \dfrac{1}{3}{S_{ABC}}.SO = \dfrac{1}{3}.3\sqrt {27} .\sqrt {52} \approx 37,47c{m^3}\)
soanvan.me
