Đề bài
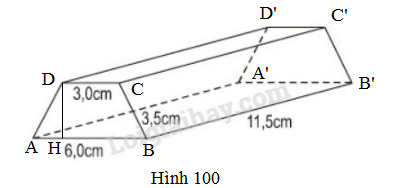
Tính diện tích toàn phần của thanh gỗ như ở hình 142 (mặt trước, mặt sau của thanh gỗ là những hình thang cân, bốn mặt còn lại đều là những hình chữ nhật, cho biết (\(\sqrt {10} \approx 3,16\)).
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích toàn phần :
\({S_{tp}} = {S_{xq}} + 2{S_đ}\)
Lời giải chi tiết
Thanh gỗ dạng hình lăng trụ đứng tứ giác, đáy là hình thang cân ABCD có \(AB=6cm, CD=3cm\) và cạnh bên \(BC=3,5cm.\) Kẻ thêm đường cao \(DH\) của hình thang cân ABCD, ta có:
\(\eqalign{
& AH = {1 \over 2}\left( {AB - CD} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}\left( {6 - 3} \right) = 1,5\left( {cm} \right) \cr} \)
Áp dụng định lí Py-ta-go đối với tam giác vuông \(ADH\), ta có:
\(DH = \sqrt {AD^2 - AH^2} =\sqrt {3,{5^2} - 1,{5^2}} \)\(\,= \sqrt {12,25 - 2,25} \) \(= \sqrt {10} \approx 3,16\left( {cm} \right)\)
\(S_{đáy}=S_{ABCD}=\dfrac{1}2(AB+CD).DH\)\(\approx \dfrac{1}2{\left( {3 + 6} \right).3,16} = 14,22c{m^2}\)
\({S_{xq}}= 2ph = (3 + 6 + 3,5 + 3,5).11,5\)\(\,=16.11,5 = 184 \,(cm^2)\)
\({S_{tp}} = {S_{xq}} + 2{S_{đáy}}\)\(\,\approx 184 + 2.14,22 = 212,44 \,(cm^2)\)
soanvan.me