Đề bài
Gọi \(O\) là điểm nằm trong hình bình hành \(ABCD.\) Chứng minh rằng tổng diện tích của hai tam giác \(ABO\) và \(CDO\) bằng tổng diện tích của hai tam giác \(BCO\) và \(DAO.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích tam giác, diện tích hình bình hành.
Lời giải chi tiết
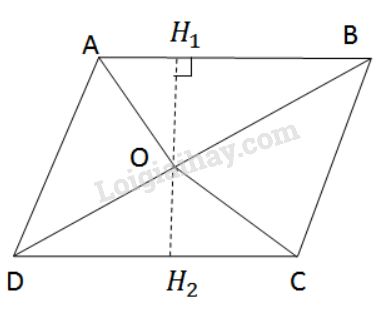
Từ \(O\) kẻ đường thẳng \(d\) vuông góc với \(AB\) ở \({H_1}\), cắt \(CD\) ở \({H_2}.\)
Ta có \(O{H_1} ⊥ AB\) (theo cách vẽ)
Mà \(AB // CD\) (vì \(ABCD\) là hình bình hành)
Nên \(O{H_2} ⊥ CD\)
Do đó \({S_{ABO}} + {S_{CDO}} \)
\( = \dfrac{1}{2}O{H_1}.AB + \dfrac{1}{2}O{H_2}.CD\)
\( = \dfrac{1}{2}O{H_1}.AB + \dfrac{1}{2}O{H_2}.AB\) (vì \(AB=CD\))
\(= \dfrac{1}{2}AB\left( {O{H_1} + O{H_2}} \right)\)
\(= \dfrac{1}{2}.AB.{H_1}{H_2}\)
\( \Rightarrow {S_{ABO}} + {S_{CDO}} = \dfrac{1}{2}{S_{ABCD}}\) ( 1) (do \(S_{ABCD}=H_1H_2.AB)\)
Mà \({S_{BCO}} + {S_{DAO}}+{S_{ABO}} + {S_{CDO}} ={S_{ABCD}}\)
Suy ra \({S_{BCO}} + {S_{DAO}} = \dfrac{1}{2}{S_{ABCD}}\) (2)
Từ (1) và (2) suy ra:
\({S_{ABO}} + {S_{CDO}} = {S_{BCO}} + {S_{DAO}}\)
soanvan.me
