Đề bài
Cho tam giác \(ABC.\) Gọi \(M, N\) là các trung điểm tương ứng của \(AC, BC.\) Chứng minh rằng diện tích của hình thang \(ABNM\) bằng \(\dfrac{3}{4}\) diện tích của tam giác \(ABC.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$$S = {1 \over 2}ah$$
Lời giải chi tiết
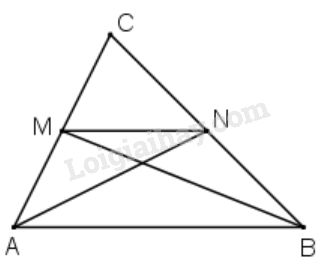
Vẽ hai trung tuyến \(AN, BM\) của \(∆ABC.\) Ta có:
\({S_{MNA}} =\dfrac{1}{2}{S_{ACN}}\)
(có cùng đường cao từ đỉnh \(N\), đáy \(AM = \dfrac{1}{2}AC)\)
\({S_{ACN}} =\dfrac{1}{2}{S_{ABC}}\)
(có cùng đường cao từ đỉnh \(A\), đáy \(CN = \dfrac{1}{2}BC)\)
\({S_{ABN}} =\dfrac{1}{2}{S_{ABC}}\)
(có cùng đường cao từ đỉnh \(A\), đáy \(BN = \dfrac{1}{2}BC)\)
Suy ra \({S_{AMN}}= \dfrac{1}{2}{S_{ACN}} =\dfrac{1}{2}.\dfrac{1}{2}{S_{ABC}}\)\(=\dfrac{1}{4}{S_{ABC}}\)
Vậy \({S_{ABN}} + {S_{AMN}} = \dfrac{1}{2}{S_{ABC}} +\dfrac{1}{4}{S_{ABC}} \)\(=\dfrac{3}{4}S_{ABC}\)
Tức là \({S_{ABNM}} = \dfrac{3}{4}{S_{ABC}}\)
soanvan.me
