Đề bài
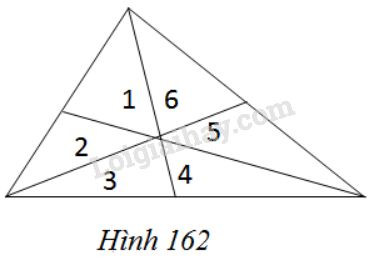
Vẽ ba đường trung tuyến của một tam giác (h.\(162\)). Chứng minh sáu tam giác: \(1, 2, 3, 4, 5, 6\) có diện tích bằng nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$$S = {1 \over 2}ah$$
Lời giải chi tiết
Theo tính chất của trung tuyến, suy ra:
\({S_1} = {S_2}\) (có đáy bằng nhau và cùng chiều cao) (1)
\({S_3} = {S_4}\) (có đáy bằng nhau và cùng chiều cao) (2)
\({S_5} = {S_6}\) (có đáy bằng nhau và cùng chiều cao) (3)
Lại có: \({S_1} + {S_2} + {S_3} = {S_4} + {S_5} + {S_6}\)\(\left( { = \dfrac{1}{2}{S_{ABC}}} \right)\) (4)
Kết hợp (4) với (1), (2), (3) suy ra \({S_1} + {S_1} + {S_3} = {S_4} + {S_6} + {S_6}\)
\(\Rightarrow 2{S_1} + {S_3} = {S_4} + 2{S_6}\)
\(\Rightarrow 2{S_1}=2{S_6}\) (do \({S_3} = {S_4}\))
\(\Rightarrow {S_1} = {S_6}\) (4’)
Và \({S_1} + {S_2} + {S_6} = {S_3} + {S_4} + {S_{5}}\)\(\left( { =\dfrac{1}{2}{S_{ABC}}} \right)\) (5)
Kết hợp (5) với (1), (2), (3) suy ra \({S_2} + {S_2} + {S_6} = {S_3} + {S_3} + {S_{5}}\)
\(\Rightarrow 2{S_2} + {S_6} = 2{S_3} + {S_5}\)
\(\Rightarrow 2{S_2}=2{S_3}\) (do \({S_6}= {S_5}\))
\(\Rightarrow {S_2} = {S_3}\) (5’)
Từ (4’), (5’) và kết hợp với (1), (2), (3) ta có :
\({S_1} = {S_2} = {S_3} = {S_4} = {S_5} = {S_6}\)
Hay \(6\) tam giác có diện tích bằng nhau.
soanvan.me
