Đề bài
Hai cạnh của một hình bình hành có độ dài là \(6\,cm\) và \(4\,cm.\) Một trong các đường cao có độ dài là \(5\,cm.\) Tính độ dài đường cao kia.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.
\(S = ah\)
Lời giải chi tiết
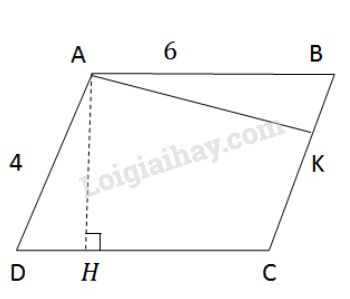
Cho hình bình hành \(ABCD\). Gọi \(AH, AK\) lần lượt là đường cao kẻ từ \(A\) đến \(CD, BC.\)
Ta có: \({S_{ABCD}} = AB.AH = AD.AK\)
\({S_{ABCD}} = 6.AH = 4.AK\)
Xét \(\Delta ABK\) vuông tại \(K\) nên \(AK<AB\) do đó \(AK < 6\).
Xét \(\Delta ADH\) vuông tại \(H\) nên \(AH<AD\) do đó \(AH<4\).
Đường cao có độ dài \(5 \,cm\) thì đó là \(AK\), không thể là \(AH\) vì \(AH < 4.\)
Vậy \(6.AH = 4.5 = 20 \)
\(\Rightarrow AH = \dfrac{{20}}{6}=\dfrac{{10}}{3}\,\,\left( {cm} \right)\)
soanvan.me
