Đề bài
Cho tam giác \(ABC\) có các cạnh \(AB= 24cm, AC = 28cm.\) Tia phân giác của góc \(A\) cắt cạnh \(BC\) tại \(D\). Gọi \(M,N\) theo thứ tự là hình chiếu của \(B\) và \(C\) trên \(AD\).
a) Tính tỉ số \(\dfrac{BM}{CN}\)
b) Chứng minh rằng \(\dfrac{AM}{AN} = \dfrac{DM}{DN}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
- Định lí: Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp đó bằng nhau, thì hai tam giác đồng dạng.
- Tính chất 2 tam giác đồng dạng.
Lời giải chi tiết
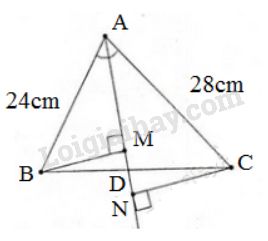
a) AD là đường phân giác của ∆ABC (gt)
\( \Rightarrow \dfrac{DB}{DC} = \dfrac{AB}{AC}\) (tính chất đường phân giác của tam giác)
\( \Rightarrow \dfrac{DB}{DC} = \dfrac{24}{28} = \dfrac{6}{7}\)
Mà \(BM // CN\) (cùng vuông góc với AD).
\( \Rightarrow ∆BMD ∽ ∆CND\) (Theo định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho)
\( \Rightarrow \dfrac{BM}{CN} = \dfrac{BD}{CD}\) (tính chất 2 tam giác đồng dạng)
Vậy \(\dfrac{BM}{CN} = \dfrac{6}{7}\)
b) \(∆ABM\) và \(∆ACN\) có:
\(\widehat{BAM} = \widehat{CAN}\) (\(AD\) là phân giác)
\(\widehat{BMA} = \widehat{CNA}= {90^o}\)
\( \Rightarrow ∆ABM ∽ ∆ACN\) (g-g)
\( \Rightarrow \dfrac{AM}{AN} = \dfrac{AB}{AC}\) (1) (tính chất 2 tam giác đồng dạng)
Mà \(\dfrac{AB}{AC} = \dfrac{DB}{DC}\) (2) (chứng minh câu a)
và \(\dfrac{BD}{CD} = \dfrac{DM}{DN}\) (3) (do \(∆BMD ∽ ∆CND\))
Từ (1), (2) và (3) \( \Rightarrow \dfrac{AM}{AN} = \dfrac{DM}{DN}\)
soanvan.me
