Video hướng dẫn giải
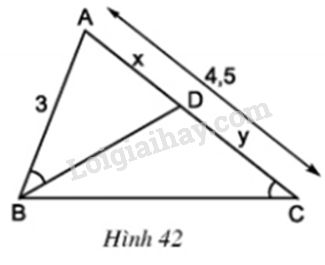
Ở hình 42 cho biết \(AB = 3cm\); \(AC = 4,5cm\) và \(\widehat {ABD} = \widehat {BCA}\)
LG a
Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?
Phương pháp giải:
Áp dụng:
- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Trong hình vẽ có \(3\) tam giác: \(ΔABD, ΔCBD, ΔABC\).
\(ΔABD\) và \(ΔACB\) có
\(\widehat B = \widehat C\)
\(\widehat A\) chung
\(⇒ ΔABD ∽ ΔACB\) (g.g)
LG b
Hãy tính các độ dài \(x\) và \(y\) (\(AD = x, DC = y\)).
Phương pháp giải:
Áp dụng: Tính chất hai tam giác đồng dạng
Lời giải chi tiết:
Vì \(ΔABD ∽ ΔACB\)
\(\eqalign{& \Rightarrow {{AB} \over {AD}} = {{AC} \over {AB}}\cr}\) ( cặp cạnh tương ứng tỉ lệ)
\(\Rightarrow {3 \over {AD}} = {{4,5} \over 3}\\ \Rightarrow AD = x = {{3.3} \over {4,5}} = 2 cm\)
\(⇒ y = 4,5 - 2 = 2,5 cm\)
LG c
Cho biết thêm \(BD\) là tia phân giác của góc \(B\). Hãy tính độ dài các đoạn thẳng \(BC\) và \(BD\).
Phương pháp giải:
Áp dụng: Tính chất đường phân giác trong tam giác.
Lời giải chi tiết:
\(BD\) là tia phân giác của góc \(B\)
\(\eqalign{ & \Rightarrow {{AB} \over {BC}} = {x \over y} \cr} \) ( Tính chất đường phân giác của tam giác)
\(\Rightarrow {3 \over {BC}} = {2 \over {2,5}}\\ \Rightarrow BC = {{3.2,5} \over 2} = 3,75 cm\)
Ta có:
\(\Delta ABD ∽\Delta ACB \Rightarrow {{AB} \over {BD}} = {{AC} \over {BC}}\)(cặp cạnh tương ứng tỉ lệ)
\(\Rightarrow {3 \over {BD}} = {{4,5} \over {3,75}}\\ \Rightarrow BD = {{3.3,75} \over {4,5}} = 2,5 cm\)
