Đề bài
Hai tam giác \(ABC\) và \(DEF\) có \(\widehat{A} = \widehat{D}, \widehat{B} = \widehat{E}\), \(AB = 8cm, BC = 10cm, DE= 6cm\). Tính độ dài các cạnh \(AC, DF\) và \(EF\), biết rằng cạnh \(AC\) dài hơn cạnh \(DF\) là \(3\,cm\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng
- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Tính chất hai tam giác đồng dạng.
Lời giải chi tiết
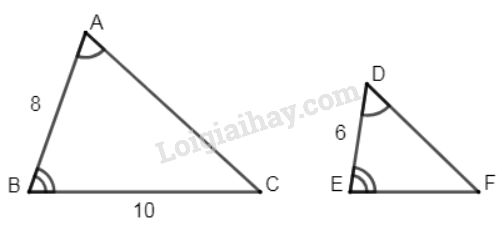
Xét \(∆ABC\) và \(∆DEF\) có:
\(\widehat{A} = \widehat{D}\) (giả thiết)
\(\widehat{B} = \widehat{E}\) (giả thiết)
\(\Rightarrow ∆ABC ∽ ∆DEF (g - g)\)
\( \Rightarrow \dfrac{AB}{DE}= \dfrac{BC}{EF} = \dfrac{CA}{FD}\) (tính chất hai tam giác đồng dạng)
Hay \(\dfrac{8}{6} = \dfrac{10}{EF} = \dfrac{CA}{FD}\)
Suy ra: \(EF = 6.10 : 8 = 7,5 cm\)
Vì \(\dfrac{8}{6} = \dfrac{CA}{FD}\)
\( \Rightarrow \dfrac{CA}{8} = \dfrac{FD}{6} = \dfrac{CA - FD}{8-6}= \dfrac{3}{2}\) (Tính chất của dãy tỉ số bằng nhau).
\( \Rightarrow CA = \dfrac{8.3}{2} = 12 cm\)
\(FD = 12 -3 = 9cm \)
soanvan.me
