Đề bài
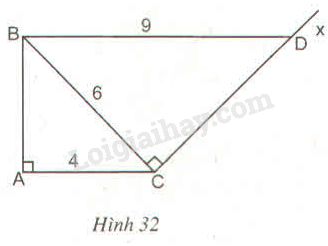
Cho tam giác \(ABC\) vuông tại \(A, \;AC = 4cm, BC = 6cm.\) Kẻ tia \(Cx\) vuông góc với \(BC\) (tia \(Cx\) và điểm \(A\) khác phía so với đường thẳng \(BC\)).Lấy trên tia \(Cx\) điểm \(D\) sao cho \(BD = 9cm\) (h.32)
Chứng minh rằng \(BD // AC.\)
Phương pháp giải - Xem chi tiết
Sử dụng: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết
\(\displaystyle {{AC} \over {CB}} = {4 \over 6} = {2 \over 3}\)
\(\displaystyle{{CB} \over {BD}} = {6 \over 9} = {2 \over 3}\)
\( \Rightarrow \displaystyle{{AC} \over {CB}} = {{CB} \over {BD}}\)
Xét hai tam giác vuông \(ABC\) và \(CDB\) có:
\(\widehat {BAC} = \widehat {DCB} = 90^\circ \)
\( \displaystyle {{AC} \over {CB}} = {{CB} \over {BD}}\) (chứng minh trên)
\( \Rightarrow ∆ ABC \backsim ∆ CDB\) (cạnh huyền và cạnh góc vuông tỉ lệ).
\( \Rightarrow \widehat {ACB} = \widehat {CBD}\)
Mà \(\widehat {ACB} \) và \( \widehat {CBD}\) ở vị trí so le trong nên \(AC // BD \).
soanvan.me
