Đề bài
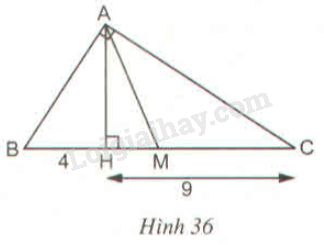
Tam giác vuông \(ABC\) (\(\widehat A = 90^\circ \)) có đường cao \(AH\) và trung tuyến \(AM\) (h.36). Tính diện tích tam giác \(AMH\), biết rằng \(BH = 4cm, CH = 9cm.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết
Xét hai tam giác vuông \(HBA\) và \(HAC\) có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat {HBA} = \widehat {HAC}\) (vì hai góc cùng phụ với \(\widehat C\))
\( \Rightarrow ∆ HBA \backsim ∆ HAC\) (g.g)
\( \Rightarrow \displaystyle {{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow H{A^2} = HB.HC = 4.9 = 36\)
\( \Rightarrow AH = 6\;(cm)\).
Vì \(AM\) là trung tuyến nên \(M\) là trung điểm của \(BC\) do đó \(\displaystyle BM = {1 \over 2}BC = {1 \over 2}.\left( {9 + 4} \right) \)\(\,=6,5\; (cm)\)
Mà \(HM = BM - BH = 6,5 - 4 \)\(\,= 2,5\; (cm)\).
Vậy \(\displaystyle {S_{AHM}} = {1 \over 2}AH.HM = {1 \over 2}.6.2,5 \)\(\,= 7,5\,(c{m^2})\).
soanvan.me
