Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), chân \(H\) của đường cao \(AH\) chia cạnh huyền \(BC\) thành hai đoạn có độ dài \(4cm\) và \(9cm.\)
Gọi \(D\) và \(E\) là hình chiếu của \(H\) trên \(AB\) và \(AC.\)
a) Tính độ dài \(DE\).
b) Các đường thẳng vuông góc với \(DE\) tại \(D\) và \(E\) cắt \(BC\) theo thứ tự tại \(M\) và \(N\). Chứng minh \(M\) là trung điểm của \(BH ,\) \(N\) là trung điểm của \(CH.\)
c) Tính diện tích tứ giác \(DENM.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Công thức tính diện tích hình thang: \(S = \dfrac{1}{2}\left( {a + b} \right).h\)
Trong đó: \(a,b\) là độ dài hai đáy hình thang, \(h\) là chiều cao.
Lời giải chi tiết
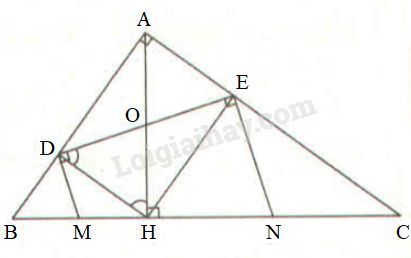
a) Xét hai tam giác vuông \(ABH\) và \(CAH\) có:
\(\widehat {ABH} = \widehat {CAH}\) (cùng phụ với \(\widehat {BAH}\))
\(\widehat {AHB} = \widehat {CHA} = {90^o}\)
\(\Rightarrow ∆ ABH\) đồng dạng \(∆ CAH\) (g.g).
\( \Rightarrow\displaystyle {{AH} \over {CH}} = {{BH} \over {AH}}\)
\( \Rightarrow A{H^2} = BH.CH \)
\(\Rightarrow AH=\sqrt {BH.CH} = \sqrt {4.9} \)\(\,= 6\,(cm) \)
Mặt khác, \(HD ⊥ AB\) và \(HE ⊥ AC\) nên \(\widehat {ADH} = \widehat {AEH} = \widehat {DAE} = {90^0}\)
Do đó, \(ADHE \) là hình chữ nhật.
Suy ra: \(DE = AH = 6 \;(cm)\) (hình chữ nhật có hai đường chéo bằng nhau).
b) Ta có:
\(\begin{array}{l}
\widehat {MDH} = {90^o} - \widehat {ODH}\\
\widehat {MHD} = {90^o} - \widehat {OHD}
\end{array}\)
Mà \(ADHE \) là hình chữ nhật nên \(OD=OH=\dfrac{AH}{2}=\dfrac{DE}{2}\)
Suy ra tam giác \(ODH\) cân tại \(O\) nên \(\widehat {ODH} = \widehat {OHD}\).
Do đó \(\widehat {MDH} = \widehat {MHD}\).
Xét tam giác \(MDH\) có \(\widehat {MDH} = \widehat {MHD}\) (chứng minh trên) nên \(\Delta MDH\) cân tại \(M\), do đó \(MD = MH\) (1)
\(\begin{array}{l}
\widehat {BDM} + \widehat {MDH} = {90^o}\\
\widehat {MDH} = \widehat {MHD}\,\,(cmt)\\
\Rightarrow \widehat {BDM} + \widehat {MHD} = {90^o}
\end{array}\)
Mặt khác: \(\widehat {MBD} + \widehat {MHD} = {90^o}\) (hai góc nhọn trong tam giác vuông phụ nhau)
Do đó: \( \widehat {BDM} = \widehat {MBD}\)
Suy ra \(\Delta BDM\) cân tại \(M\) nên \(MD = BM\) (2)
Từ (1) và (2) suy ra \(M \) là trung điểm của \(BH\).
Chứng minh tương tự \(N\) là trung điểm của \(CH.\)
c) Theo chứng minh trên, ta có:
\(DM = MH \displaystyle= {1 \over 2}BH = \displaystyle{1 \over 2}.4 = 2(cm) \)
\(EN = NH \displaystyle= {1 \over 2}CH =\displaystyle {1 \over 2}.9 = 4,5\)\(\,(cm) \)
\(DE = AH = 6\,(cm) \)
Ta có \(MD//EN\) (cùng vuông góc với \(DE\)) nên \(DENM \) là hình thang.
Lại có \(\widehat {MDE}=90^0\) nên \(DENM \) là hình thang vuông, do đó diện tích của nó là:
\(\displaystyle {S_{DENM}} = {1 \over 2}\left( {DM + EN} \right)DE \)\(\,\displaystyle = {1 \over 2}.\left( {2 + 4,5} \right).6 = 19,5\,(c{m^2})\).
soanvan.me
