Video hướng dẫn giải
Thực hiện các phép tính:
LG a.
\(\left( {\dfrac{x}{{x + 1}} + 1} \right):\left( {1 - \dfrac{{3{x^2}}}{{1 - {x^2}}}} \right);\)
Phương pháp giải:
Áp dụng các phép toán cộng, trừ, nhân, chia phân thức.
Lời giải chi tiết:
\(\eqalign{
& \;\left( {{x \over {x + 1}} + 1} \right):\left( {1 - {{3{x^2}} \over {1 - {x^2}}}} \right) \cr
& = {{x + x + 1} \over {x + 1}}:{{1 - {x^2} - 3{x^2}} \over {1 - {x^2}}} \cr
& = {{2x + 1} \over {x + 1}}:{{1 - 4{x^2}} \over {1 - {x^2}}} \cr
& = {{2x + 1} \over {x + 1}}.{{1 - {x^2}} \over {1 - 4{x^2}}} \cr
& = {{2x + 1} \over {x + 1}}.{{1 - {x^2}} \over {1 - {{\left( {2x} \right)}^2}}} \cr
& = {{2x + 1} \over {x + 1}}.{{\left( {1 - x} \right)\left( {1 + x} \right)} \over {\left( {1 - 2x} \right)\left( {1 + 2x} \right)}} \cr
& = {{1 - x} \over {1 - 2x}} \cr} \)
LG b.
\(\left( {{x^2} - 1} \right)\left( {\dfrac{1}{{x - 1}} - \dfrac{1}{{x + 1}} - 1} \right)\)
Phương pháp giải:
Áp dụng tính chất nhân phân phối giữa phép nhân và phép cộng:
\(\dfrac{A}{B}\left( {\dfrac{C}{D} + \dfrac{E}{F}} \right) = \dfrac{A}{B}.\dfrac{C}{D} + \dfrac{A}{B}.\dfrac{E}{F}\)
Lời giải chi tiết:
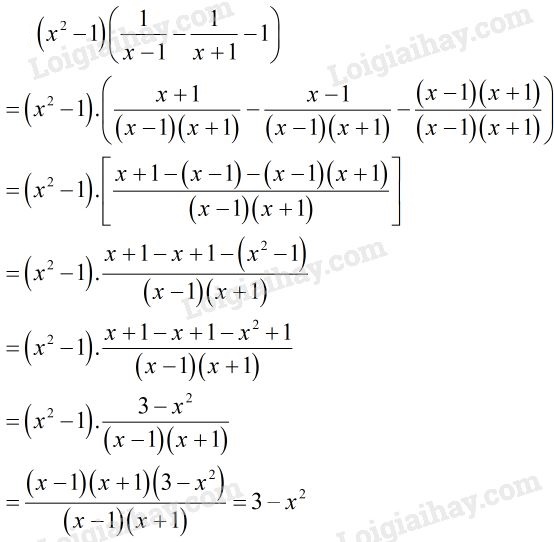
Cách 2:
Áp dụng tính chất nhân phân phối giữa phép nhân và phép cộng, phép trừ:
\(\eqalign{
& \left( {{x^2} - 1} \right)\left( {{1 \over {x - 1}} - {1 \over {x + 1}} - 1} \right) \cr
& = \left( {{x^2} - 1} \right).{1 \over {x - 1}} + \left( {{x^2} - 1} \right).{{ - 1} \over {x + 1}} + \left( {{x^2} - 1} \right)\left( { - 1} \right) \cr
& = {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {x - 1}} - {{\left( {x - 1} \right)\left( {x + 1} \right)} \over {x + 1}} - \left( {{x^2} - 1} \right) \cr
& = x + 1 - \left( {x - 1} \right) - {x^2} + 1 \cr&= x + 1 - x + 1 - {x^2} + 1\cr& = - {x^2} + 3 \cr} \)
soanvan.me
