Đề bài
a) Một hình vuông có cạnh bằng \(3cm\). Đường chéo của hình vuông đó bằng \(6cm\), \(\sqrt{18}cm\), \(5cm\) hay \(4cm\) ?
b) Đường chéo của một hình vuông bằng \(2dm\). Cạnh của hình vuông đó bằng: \(1dm, \dfrac{3}{2}dm\), \(\sqrt{2}dm\) hay \(\dfrac{4}{3}dm\)?
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết
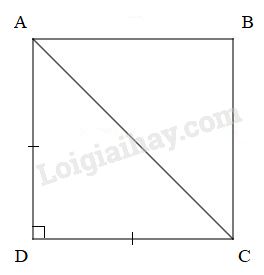
a) Áp dụng định lí Pytago vào \(\Delta ACD\) vuông tại \(D\) ta có:
\(A{C^2} = A{D^2} + D{C^2} = {3^2} + {3^2} = 18\)
Suy ra \(AC= \sqrt{18}\) (cm)
b) Đặt \(AD=DC=x\). Áp dụng định lí Pytago vào \(\Delta ADC\) vuông tại \(D\) ta có:
\(\eqalign{
& A{D^2} + D{C^2} = A{C^2} \Rightarrow {x^2} + {x^2} = {2^2} \cr
& \Rightarrow 2{x^2} = 4 \Rightarrow {x^2} = 2 \cr} \)
Suy ra \(x= \sqrt{2}\). Vậy cạnh của hình vuông bằng \(\sqrt{2}dm\).
soanvan.me
