Đề bài
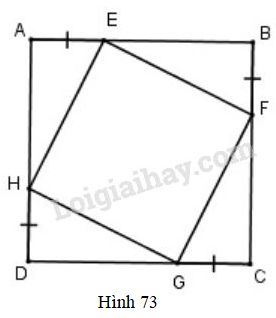
Cho hình \(73\), trong đó \(ABCD\) là hình vuông. Chứng minh rằng tứ giác \(EFGH\) là hình vuông.
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Dấu hiệu nhận biết hình thoi: Tứ giác có \(4\) cạnh bằng nhau là hình thoi.
+) Dấu hiệu nhận biết hình vuông: Hình thoi có một góc vuông là hình vuông.
Lời giải chi tiết
Theo tính chất hình vuông, ta có:
\(AB=BC=CD=DA\)
Theo giả thiết, \(AE = BF = CG = DH\)
Suy ra \(EB=FC=GD=HA\)
\(∆AEH \) và \( ∆BFE\) có:
\(AE = BF \) (gt)
\(HA=EB\) (chứng minh trên)
\(\widehat A = \widehat B = {90^o}\)
Do đó \(∆AEH = ∆BFE \) (c.g.c), suy ra \(HE=EF\) (hai cạnh tương ứng).
Chứng minh tương tự ta có \(EF=FG, FG=GH, GH=HE\)
Tứ giác \(EFGH\) có \(HE = EF = FG = GH\) nên là hình thoi (1)
\(∆AEH = ∆BFE \) (chứng minh trên) suy ra \(\widehat{AEH} = \widehat{BFE}\) (hai góc tương ứng)
Ta lại có \(\widehat {BEF} + \widehat {BFE} = {90^o}\) nên \(\widehat {AEH} + \widehat {BEF} = {90^o}\) suy ra \(\widehat {HEF} = {90^o}\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông (hình thoi có một góc vuông là hình vuông).
soanvan.me
