Đề bài
Cho đường tròn đường kính \(AB.\) Qua \(A\) và \(B\) kẻ hai tiếp tuyến của đường tròn đó. Gọi \(M\) là một điểm trên đường tròn. Các đường thẳng \(AM\) và \(BM\) cắt các tiếp tuyến trên lần lượt tại \(B’\) và \(A’.\)
\(a)\) Chứng minh rằng \({\rm{AA}}'.BB' = A{B^2}\)
\(b)\) Chứng minh rằng \(A'{A^2} = A'M.A'B\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Nếu hai tam giác đồng dạng ta suy ra các cạnh tương ứng tỉ lệ.
+) Góc nội tiếp chắn nửa đường tròn là góc vuông.
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Lời giải chi tiết
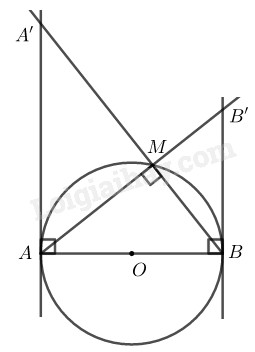
\(a)\) Xét \(∆AA'B\) và \(∆BB'A:\)
\(\widehat {A'AB} = \widehat {B'BA} = {90^0}\)
\(\widehat {BB'A} = \widehat {ABA'}\) (vì cùng phụ với \(\widehat {BAB'}\))
Suy ra: \(∆AA'B\) đồng dạng \(∆BAB'\; (g.g)\)
\(\displaystyle {{AA'} \over {BA}} = {{AB} \over {BB}} \Rightarrow AA'.BB' = A{B^2}\)
\(b)\) \(\widehat {AMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow AM \bot A'B\)
\(∆AA'B\) vuông tại \(A.\) Theo hệ thức lượng trong tam giác vuông ta có:
\(AA{'^2} = A'M.A'B\)
soanvan.me
