Đề bài
Tam giác đều \(ABC\) nội tiếp đường tròn tâm \(O\) bán kính \(R.\) Khi đó, \(\widehat {BOC}\) có số đo bằng bao nhiêu\(?\)
\((A)\) \( 60^\circ ; \) \((B)\) \( 120^\circ ; \)
\((C)\) \( 240^\circ ; \) \( (D)\) Không tính được.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải chi tiết
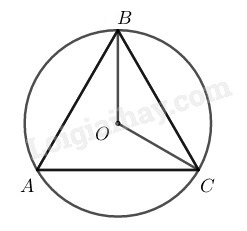
Xét đường tròn \((O),\) ta có: \(\widehat{BAC}=\dfrac{1}{2}\widehat{BOC}\) (số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung)
Nên \(\widehat{BOC}=2\widehat{BAC}=2.60^\circ=120^\circ\)
Vậy chọn \((B)\) \( 120^\circ \)
soanvan.me
