Đề bài
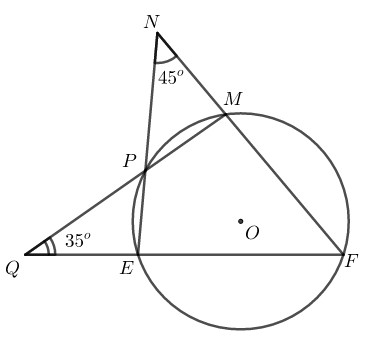
Cho hình sau. Khi đó, số đo của \(\widehat {MFE}\) bằng bao nhiêu\(?\)
\((A)\) \(50^\circ;\) \((B)\) \(80^\circ;\)
\((C)\) \(130^\circ;\) \( (D)\) Không tính được.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.
Lời giải chi tiết
Xé đường tròn \((O),\) ta có: \(\widehat{MFE}= \dfrac{1}{2}sđ\overparen{ME}(nhỏ)\) (góc nội tiếp)
\(=\dfrac{1}{2}(sđ \overparen{PM} +sđ \overparen{PE})\)
Ta có:
+) \(\widehat{N}=\dfrac{1}{2}(sđ \overparen{EF} -sđ \overparen{PM})\) (góc có đỉnh bên ngoài đường tròn)
\(\Rightarrow sđ \overparen{EF}=2\widehat{N}+ sđ \overparen{PM}\)
+) \(\widehat{Q}=\dfrac{1}{2}(sđ \overparen{MF} -sđ \overparen{PE})\) (góc có đỉnh bên ngoài đường tròn)
\(\Rightarrow sđ \overparen{MF}=2 \widehat{Q}+sđ \overparen{PE}\)
\(\Rightarrow sđ \overparen{MF}+sđ\overparen{EF}\)\(=2 (\widehat{Q}+\widehat{N})+(sđ \overparen{PE}+sđ \overparen{PM})\)
\(\Rightarrow sđ \overparen{ME}(lớn)\)\(= 2 (\widehat{Q}+\widehat{N})+sđ \overparen{ME}(nhỏ)\)
Mà \(sđ \overparen{ME}(lớn)=360^\circ-sđ \overparen{ME}(nhỏ)\)
\(\Rightarrow 360^\circ-sđ \overparen{ME}(nhỏ)\)\(= 2 (\widehat{Q}+\widehat{N})+sđ \overparen{ME}(nhỏ)\)
\(\Rightarrow sđ \overparen{ME}(nhỏ) =180^\circ-(\widehat{Q}+\widehat{N})\)\(=180^\circ-(35^\circ+45^\circ)=100^\circ\)
Do đó: \(\widehat{MFE}= \dfrac{1}{2}sđ\overparen{ME}(nhỏ)\)\(= \dfrac{1}{2}.100^\circ=50^\circ\)
Vậy chọn \((A)\) \(50^\circ\)
soanvan.me
